Unity implements smooth interpolation

For those unfamiliar with Unity For people who , We all know that each script has three callable update Handle . When update processing is required, you can call Update, You can also call a better LateUpdate. Both of these use global variables Time.deltaTime To access the time interval between frames .FixedUpdate Use Time.fixedTimeDelta And run in a fixed time step , Therefore, each frame may be run many times .

The original English text

About important Lerp problem .

This question seems to be asked again and again on the forum , How to achieve perfectly smooth interpolation and damping Damping. For example, you have a value a, And you want to smoothly interpolate it to another value b, You decide to use arbitrary interpolation coefficients r Linear interpolation . If you are in a variable frame rate function （Update or LateUpdate） A similar operation is performed in , Then you will encounter the following problems ：

1 individual

a = Mathf.Lerp(a, b, r);

There's something wrong with this code , Because it is in Of each frame a and b  And we know that the frame rate is variable , So smoothness is variable .

Once this is clear , Maybe we can do some research , stay Unity In the document You will find it advisable to do so ：

1 individual

a = Mathf.Lerp(a, b, r * Time.deltaTime);

wait a moment , This is not quite right ... The interpolation coefficient may now exceed 1, This is not allowed . This is not allowed . What about next ？ Let's consider not using primitive lerp, Do not apply deltatime 了 , But this time put it in FixedUpdate in , Use fixdeltatime.

But there are still potential problems . It's a little subtle , Because in FixedUpdate Something that runs in will almost never be in the correct state of the current frame , Because the update rate is different . This means that they need extrapolation or interpolation to achieve smooth display .Unity There is an option to enable extrapolation or interpolation for rigid bodies , therefore , If you enable this option and want to constrain rigid body attributes , Then the rigid body will work as expected . however , If you are not using extrapolation or interpolation , Then FixedUpdate for , Smoothing is technically smooth , But you will still see the Caton phenomenon on the screen .

Another problem that cannot be avoided with fixed updates is , If you need to change the update rate （ for example , Would you like to 100 Hz The frequency of running Physics ） And use common lerp, You need to readjust the smoothing value .

What are we trying to do ？

Let's simplify a few things , Let's see what we actually want to achieve here . Now? , Let's assume that we always interpolate to zero .

One way to solve this problem is to ask how many initial values should be retained after one second . Suppose our initial value is 10, Every second we lose half of our current value ：

  

Let's look at its graph over time . We can see , From the starting value 10 To almost zero , This is a smooth curve . It will never reach zero completely , But it will be very close to zero .

View the number sequence , We can easily sum it up as ：

  

Or for （0,1） Any ratio in the range r：

  

If we are one step ahead of the current value , What's going to happen ？  

 

I hope the pattern here is clear , So we can say more generally ：

  

This means that we can t Value , And in the future t + n in Calculate the value at any time . It must be realized here that n It doesn't have to be an integer value , So use... Here deltaTime very good . This means that we can now write a frame rate sensing function , This function will decay to zero , And use it in the variable rate update function

1 individual 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 year

// Smoothing rate dictates the proportion of source remaining after one second // publicstaticfloatDamp(floatsource, floatsmoothing, floatdt) {     returnsource * Mathf.Pow(smoothing, dt); }   privatevoidUpdate() {     a = Damp(a, 0.5f, Time.deltaTime); }   // or   privatevoidFixedUpdate() {     a = Damp(a, 0.5f, Time.fixedDeltaTime); }

If you interpolate in a specified range ？

If you want to value a Change to value b Not zero ？ The key here is , It's just a graph in y Translate on the axis . If we start from 20 Decay to 10, Then it looks like this ：

therefore , We need to use （a – b） Add damping , Then add b. Let's change the damping function to do this ：

  

This should look familiar …… Its form and standard Lerp identical , but rate Parameter has exponent ：

1 individual

a(t + n) = Lerp(b, a(t), Pow(r, n))

You may notice here that these parameters do not match the order you expect , But it's easy to solve , because ：

1 individual

Lerp(a, b, t) = Lerp(b, a, 1 - t)

therefore ：

1 individual

a(t + n) = Lerp(a(t), b, 1 - Pow(r, n))

We can write this code directly , Or a better idea is to wrap it in a function , This function will perform frame rate aware damping between two arbitrary values ：

1 individual 2 3 4 5 6

// Smoothing rate dictates the proportion of source remaining after one second // publicstaticfloatDamp(floatsource, floattarget, floatsmoothing, floatdt) {     returnMathf.Lerp(source, target, 1 - Mathf.Pow(smoothing, dt)) }

A smoothing rate of zero will return you the target value （ That is, no smoothing ）, Technically, the impermissible rate is 1, Only the source value will be returned to you （ That is, infinite smoothing ）. Please note that , This is related to lerp Parameters work the opposite way , But if you want to , Can be in Pow Inverse addition using smoothing parameters in .

Exponential decay

The keen eyes among you may have seen the picture , And think it looks very much like an exponential decay function . You will be right , Because it actually yes Exponential decay function . Understand why , Let's go back to not taking b Damping function of ：

  

Now? , Compare it with the exponential decay formula ：

  

Let's equate it with , See what happens

  

therefore

  

therefore , Another way to express the damping function is to use lambda A parameterized . Now it ranges from zero to infinity , Well expressed the fact that , That is, you can never really achieve b.

1 individual 2 3 4

publicstaticfloatDamp(floata, floatb, floatlambda, floatdt) {     returnMathf.Lerp(a, b, 1 - Mathf.Exp(-lambda * dt)) }

If you look at other codes , You will see the usual form of exponential decay , But I only know that it is frame rate aware Lerp Another form of （ vice versa , It depends on how you think about it ）.

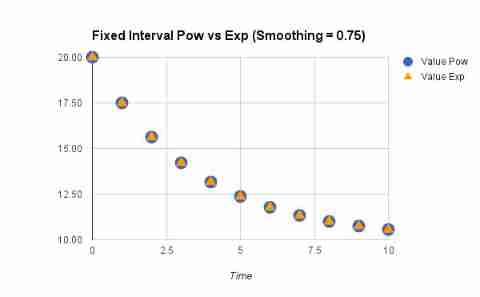
The following figure shows the two forms of λ damping . As you can see , They all match perfectly .

 

 

 

Last , This is the same picture , But this time it's a random interval .

Abstract

• Not in Update or FixedUpdate Internal use of ordinary Lerp Damping .
• stay FixedUpdate Use in Lerp Be careful , And ensure that the results will be interpolated or extrapolated .
• As far as possible , Even in FixedUpdate in , It is best to use the frame rate sensing damping function , Because it will allow you to change the fixed update rate without readjusting the damping .

I hope this will eliminate the need for proper use of damping values Lerp Some puzzles of .