当前位置:网站首页>完全背包问题
完全背包问题
2022-08-03 10:45:00 【hnjzsyjyj】
【题目来源】
https://www.acwing.com/problem/content/description/3/
【问题描述】
有 N 种物品和一个容量是 V 的背包,每种物品都有无限件可用。
第 i 种物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
【输入格式】
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 种物品的体积和价值。
【输出格式】
输出一个整数,表示最大价值。
【数据范围】
0<N,V≤1000
0<vi,wi≤1000
【算法分析】
背包问题,求解的是“将某些种物品装入背包,......”,而不是求解“将某些个物品装入背包,......”的问题。切记。
完全背包问题,类似于0-1背包问题,依然是求解“将哪些种物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大”。故依然可设 c[i][j] 为将前 i 种物品装入容量为 j 的背包中所获得的最大价值,vol[i] 为第 i 中物品的体积,val[i] 为第 i 种物品的价值。但由于其特殊性,即在完全背包问题中的每种物品有无限多个,而0-1背包问题中的每种物品只有一个,故在利用“最后一步法”构建完全背包问题的状态转移方程时,针对第 i 种物品,可能会选择0,1,2,... ,k个(k*vol[i]<=j)。之所以会选到 k 个,而不是无限多个,原因在于虽然完全背包问题中每种物品都有无限多个,但受到背包容量的限制,只可能装有限个。
完全背包问题的视频讲解可参考:https://www.bilibili.com/video/BV16F411M7CU
思路详见下图:

可见依据上图的分析思路,则完全背包问题的代码将会有三重循环,必然导致代码复杂度增加。同时,这也必然会导致时间复杂度剧增,有可能会TLE。因此,需要进行优化。
将完全背包问题的状态转移方程写在下方:
c[i][j]=max(c[i-1][j],c[i-1][j-vol[i]]+val[i], ..., c[i-1][j-(k-1)*vol[i]]+(k-1)*val[i], c[i-1][j-k*vol[i]]+k*val[i]),
令 j=j-vol[i],并考虑到 k*vol[i]<=j,则有
c[i][j-vol[i]]=max(c[i-1][j-vol[i]],c[i-1][j-vol[i]-vol[i]]+val[i], ..., c[i-1][j-vol[i]-(k-1)*vol[i]]+(k-1)*val[i])
=max(c[i-1][j-vol[i]],c[i-1][j-2*vol[i]]+val[i], ..., c[i-1][j-k*vol[i]]+(k-1)*val[i])
推出完全背包问题的状态转移方程 c[i][j]=max(c[i-1][j], c[i][j-vol[i]]+val[i]),这样就优化为二维了。
类比于0-1背包问题的状态转移方程 c[i][j]=max(c[i-1][j],c[i-1][j-vol[i]]+val[i]) 优化为一维的思路,可在上面优化为二维的基础上,进一步得出完全背包问题的一维优化形式:
c[j]=max(c[j], c[j-vol[i]]+val[i]),满足 i:1~n,j:1~V 且 j>=vol[i]
若要从代码模板的角度来看的话,完全背包问题的代码只需要将0-1背包问题的一维实现代码的内层循环改为从 vol 到 V 进行遍历便可。即将0-1背包问题的一维实现中的内层循环 for(int j=V;j>=vol;j--) 改为 for(int j=vol;j<=V;j++) ,便为完全背包的代码实现。是不是有点废O(∩_∩)O哈哈~
【算法代码】
#include<bits/stdc++.h>
using namespace std;
const int maxn=1005;
int c[maxn];
int main() {
int n,V;
cin>>n>>V;
for(int i=1;i<=n;i++){
int vol,val;
cin>>vol>>val;
for(int j=vol;j<=V;j++)
c[j]=max(c[j],c[j-vol]+val);
}
cout<<c[V]<<endl;
return 0;
}
/*
in:
4 5
1 2
2 4
3 4
4 5
out:
10
*/
【参考文献】
https://www.bilibili.com/video/BV16F411M7CU
https://www.acwing.com/problem/content/description/3/
https://blog.csdn.net/hnjzsyjyj/article/details/125987923
边栏推荐
- 集成学习、boosting、bagging、Adaboost、GBDT、随机森林
- This article understands the process from RS485 sensor to IoT gateway to cloud platform
- 简述设计的意义是什么_定义和概念的最大区别
- 跨链桥协议 Nomad 遭遇黑客攻击,损失超 1.5 亿美元
- MySQL中tinytext、text、mediumtext和longtext等各个类型详解[通俗易懂]
- numpy
- 2022.8.2-----leetcode.622
- 罕见的数学天才,靠“假结婚”才得到追求事业的机会
- 开源一夏 | 教你快速实现“基于Docker快速构建基于Prometheus的MySQL监控系统”
- numpy
猜你喜欢
4G采集ModbusTCP转JSON接MQTT云平台
MySQL数据库实战(1)

面试突击71:GET 和 POST 有什么区别?
一文了解,从RS485传感器到物联网关到云平台过程
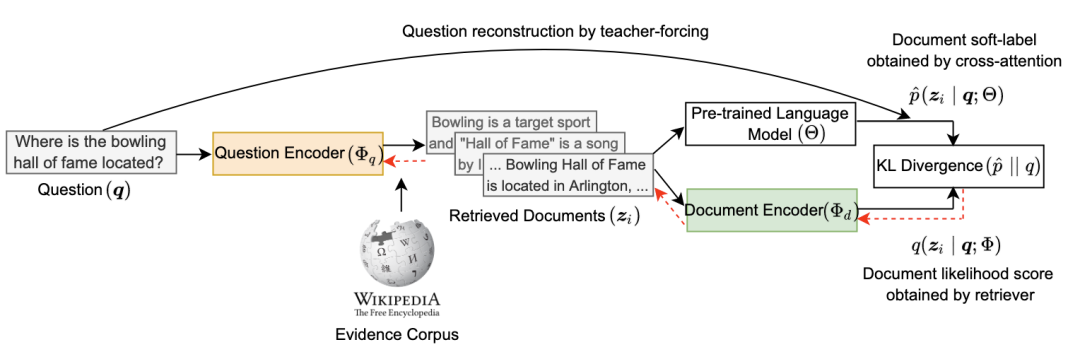
训练双塔检索模型,可以不用query-doc样本了?明星机构联合发文

4 g acquisition ModbusTCP turn JSON MQTT cloud platform
VL53L0X V2 laser ranging sensor collects distance data serial output
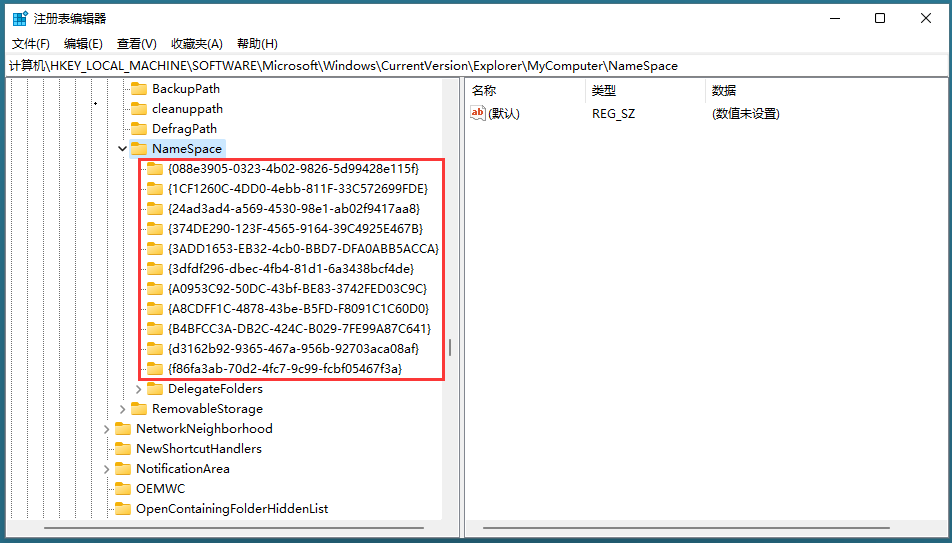
Win10/11 删除文件资源管理器左侧栏目文件夹

servlet生命周期详解--【结合源码】
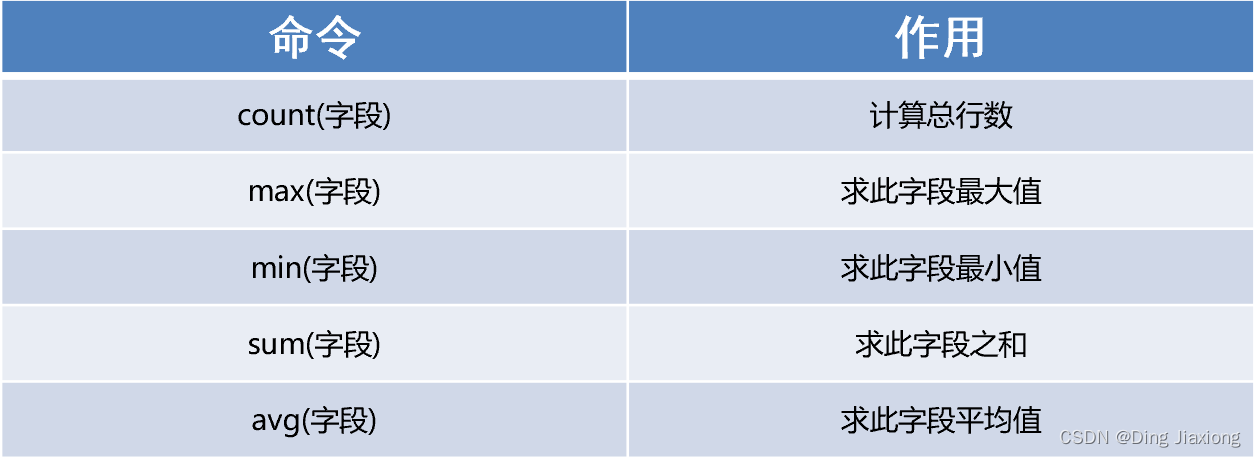
Basic using MySQL database
随机推荐
servlet生命周期详解--【结合源码】
Mysql OCP 75题
Leecode-SQL 1527. 模糊查询匹配(模糊查询用法)
全新的Uber App设计
C# Color颜色RGB对照表、颜色选择器
简述设计的意义是什么_定义和概念的最大区别
Matplotlib
怎么在外头使用容器里php命令
聊天app开发——防炸麦以及节省成本的内容鉴定方法
2022T电梯修理考试题及答案
面试一面
进入 SQL Client 创建 table 后,在另外一个节点进入 SQL Client 查询不到
成对连接点云分割
Basic using MySQL database
MATLAB程序设计与应用 2.6 字符串
混合型界面:对话式UI的未来
With strong network, China mobile to calculate excitation surging energy network construction
跨链桥协议 Nomad 遭遇黑客攻击,损失超 1.5 亿美元
This article understands the process from RS485 sensor to IoT gateway to cloud platform
【学习笔记之菜Dog学C】通讯录