当前位置:网站首页>[trio basic from introduction to mastery tutorial 20] trio calculates the arc center and radius through three points of spatial arc
[trio basic from introduction to mastery tutorial 20] trio calculates the arc center and radius through three points of spatial arc
2022-07-05 08:02:00 【Changjiang houlang blog】
brothers , Hello everyone . Today, we will bring you the formula for calculating the center and radius of the arc at three points of the space arc . stay Trio in , Integrated calculation functions , Our goal today is to realize this calculation formula by ourselves .
' Import calculation data
TABLE(100,0,0,0,5,5,5,5,0,0)
' Write your own algorithm
calcriclecen(100,FALSE)
PRINT "XYZ 1=",TABLE(100+10),TABLE(100+11),TABLE(100+12)
'Trio Original algorithm implementation
SPHERE_CENTRE(100+3, 100+6, 100+10)
PRINT "XYZ 2=",TABLE(100+10),TABLE(100+11),TABLE(100+12)Trio Instructions help

From this instruction, we can see , Its starting point must be 0,0,0, This means that the calculation must be incremental .
Let's look at our own handwriting Algorithm :
'=================================================================
'=================================================================
' Calculate the center and radius of the arc at three points in a given space
'partable Given input parameters
'Table0-2 Given P Point coordinates ( The starting point )
'Table3-5 Given Q Point coordinates ( Midpoint )
'Table6-8 Given Q Point coordinates ( End )
'Table10-13 Output arc center XYZR
'needprint Confirm whether the calculation process data needs to be printed false No printing ,true Print
FUNCTION calcriclecen(partable AS INTEGER,needprint AS BOOLEAN) AS BOOLEAN
' Input parameter check
IF partable<0 OR partable>511980 THEN
PRINT "Parameter out of range,Par=",partable
RETURN FALSE
ENDIF
' Calculate the center and radius of the arc at three points in a given space
DIM dpx,dpy,dpz AS FLOAT
dpx=TABLE(partable+0)
dpy=TABLE(partable+1)
dpz=TABLE(partable+2)
DIM dqx,dqy,dqz AS FLOAT
dqx=TABLE(partable+3)
dqy=TABLE(partable+4)
dqz=TABLE(partable+5)
DIM drx,dry,drz AS FLOAT
drx=TABLE(partable+6)
dry=TABLE(partable+7)
drz=TABLE(partable+8)
' Print process data
IF needprint THEN
PRINT "========================="
PRINT "Input Parmater:"
PRINT "P [XYZ]=",dpx,dpy,dpz
PRINT "Q [XYZ]=",dqx,dqy,dqz
PRINT "R [XYZ]=",drx,dry,drz
ENDIF
' Output space origin and radius
DIM dx0,dy0,dz0,dr AS FLOAT
DIM dx1,dy1,dz1 AS FLOAT
dx0=0
dy0=0
dz0=0
dr=0
'-------------------------------------------
DIM pi0,pj0,pk0 AS FLOAT
DIM x1,x2,y1,y2,z1,z2 AS FLOAT
x1=dqx-dpx
x2=drx-dpx
y1=dqy-dpy
y2=dry-dpy
z1=dqz-dpz
z2=drz-dpz
pi0=y1*z2-z1*y2
pj0=z1*x2-x1*z2
pk0=x1*y2-y1*x2
' Print process data
IF needprint THEN
PRINT "Proc Parmater:"
PRINT "IJK =",pi0,pj0,pk0
ENDIF
IF (pi0=0) AND (pj0=0) AND (pk0=0) THEN
STOP
ENDIF
'-------------------------------------------
' seek PQ and PR The vertical line of the line
'---------------------
'1, too PQ The midpoint of (Mx,My,Mz)
DIM dmx,dmy,dmz AS FLOAT
dmx=(dpx+dqx)/2
dmy=(dpy+dqy)/2
dmz=(dpz+dqz)/2
' And (Mi,Mj,Mk)=(pi,pj,pk)×(x1,y1,z1) vertical
DIM dmi,dmj,dmk AS FLOAT
dmi=pj0*z1-pk0*y1
dmj=pk0*x1-pi0*z1
dmk=pi0*y1-pj0*x1
IF needprint THEN
PRINT "PQ M=",dmi,dmj,dmk
ENDIF
'---------------------
'2, too PR The midpoint of (Nx,Ny,Nz)
DIM dnx,dny,dnz AS FLOAT
dnx=(dpx+drx)/2
dny=(dpy+dry)/2
dnz=(dpz+drz)/2
' And (Ni,Nj,Nk)=(pi,pj,pk)×(x2,y2,z2) vertical
DIM dni,dnj,dnk AS FLOAT
dni=pj0*z2-pk0*y2
dnj=pk0*x2-pi0*z2
dnk=pi0*y2-pj0*x2
IF needprint THEN
PRINT "PR M=",dni,dnj,dnk
ENDIF
' Combined calculation
DIM ds AS FLOAT
'ds=dNi*dNi+dNj*dNj+dNk*dNk
ds=SQR(pi0*pi0+pj0*pj0+pk0*pk0)
IF ds=0 THEN
dx1=0
dy1=0
dz1=0
ELSE
dx1=pi0/ds
dy1=pj0/ds
dz1=pk0/ds
ENDIF
IF needprint THEN
PRINT "DX1 =",dx1,dy1,dz1,ds
ENDIF
'-------------------------------------------
' The two vertical lines obtained are {X=dMx+dMi*tm;Y=dMy+dMj*tm;Z=dMz+dMk*tm;}
' or (x-dmx)/dmi=(y-dmy)/dmj=(z-dmz)/dmk
' {X=dNx+dNi*tn;Y=dNy+dNj*tn;Z=dNz+dNk*tn;}
' or (x-dnx)/dni=(y-dny)/dnj=(z-dnz)/dnk;
' Solve the intersection of two straight lines
DIM tm,tn AS FLOAT
tn=((dmy-dny)*dmi+dmj*(dnx-dmx))/(dnj*dmi-dmj*dni)
tm=(dnx+dni*tn-dmx)/dmi
'dx0,dy0,dz0,dr
dx0=INT((dmx+dmi*tm)*100000+0.5)/100000
dy0=INT((dmy+dmj*tm)*100000+0.5)/100000
dz0=INT((dmz+dmk*tm)*100000+0.5)/100000
dr=INT((SQR((dx0-dpx)*(dx0-dpx)+(dy0-dpy)*(dy0-dpy)+(dz0-dpz)*(dz0-dpz)))*100000+0.5)/100000
TABLE(partable+10,dx0,dy0,dz0,dr)
IF needprint THEN
PRINT "Out Parmater:"
PRINT "OUT X Y Z R =",dx0,dy0,dz0,dr
PRINT "========================="
ENDIF
RETURN TRUE
ENDFUNC
'=================================================================Calculate the center and radius of the arc by giving three points in space
Run the result test

The two methods are consistent !
The task of this course is over , Thank you for watching ...
边栏推荐
- UEFI development learning 2 - running ovmf in QEMU
- Global and Chinese market of blackbody calibration source 2022-2028: Research Report on technology, participants, trends, market size and share
- [professional literacy] specific direction of analog integrated circuits
- Altium Designer 19.1.18 - 更改铺铜的透明度
- Bluetooth hc-05 pairing process and precautions
- H264 (I) i/p/b frame gop/idr/ and other parameters
- Altium Designer 19.1.18 - 导入板框
- Verilog -- state machine coding method
- Global and Chinese markets for flexible endoscopic lithotripsy devices 2022-2028: Research Report on technology, participants, trends, market size and share
- Global and Chinese market of resistivity meter 2022-2028: Research Report on technology, participants, trends, market size and share
猜你喜欢
![Shape template matching based on Halcon learning [viii] PM_ multiple_ models. Hdev routine](/img/13/22a1915329f58acd54c40176f6f301.jpg)
Shape template matching based on Halcon learning [viii] PM_ multiple_ models. Hdev routine
Markdown tips

Record the visual shock of the Winter Olympics and the introduction of the screen 2
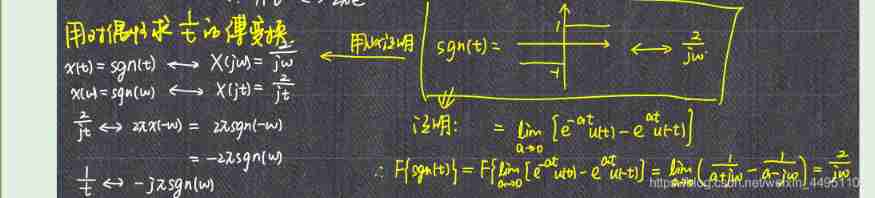
A simple method to prove 1/t Fourier transform
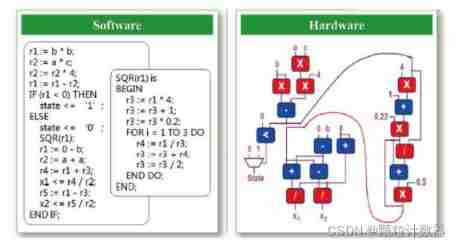
High end electronic chips help upgrade traditional oil particle monitoring
MySQL blind note common functions
![C WinForm [get file path -- traverse folder pictures] - practical exercise 6](/img/8b/1e470de4e4ecd4fd1bb8e5cf23f466.jpg)
C WinForm [get file path -- traverse folder pictures] - practical exercise 6

Altium Designer 19.1.18 - 清除测量距离产生的信息

Shell script basic syntax
Acwing-宠物小精灵之收服-(多维01背包+正序倒序+两种形式dp求答案)
随机推荐
Record the visual shock of the Winter Olympics and the introduction of the screen 2
Gradle复合构建
mysql 盲注常见函数
L'étude a révélé que le système de service à la clientèle du commerce électronique transfrontalier a ces cinq fonctions!
Global and Chinese market of urban rail connectors 2022-2028: Research Report on technology, participants, trends, market size and share
Relationship between line voltage and phase voltage, line current and phase current
[popular science] some interesting things that I don't know whether they are useful or not
Verilog -- state machine coding method
matlab timeserise
IC software learning
Correlation based template matching based on Halcon learning [II] find_ ncc_ model_ defocused_ precision. hdev
Query the table name used by kettle in Oracle
Global and Chinese market of blackbody calibration source 2022-2028: Research Report on technology, participants, trends, market size and share
Process communication mode between different hosts -- socket
How to select conductive slip ring
Win10 shortcut key
C language # and #
Live555 push RTSP audio and video stream summary (I) cross compilation
Bootloader implementation of PIC MCU
Shape template matching based on Halcon learning [9] PM_ multiple_ dxf_ models. Hdev routine -- [read and write XLD from DXF file]