Acwing-宠物小精灵之收服-(多维01背包+正序倒序+两种形式dp求答案)

宠物小精灵之收服

题意：
就是有n个宠物，捉住他们要a的体力和b的精灵球。现在你有m体力，k个精灵球。问你最多能抓住多少宠物，然后在宠物最多的情况下，最多还能剩下多少体力。

思考：
很明显这个也是可以优化掉枚举物品那一维度。然后三重循环就可以了。对于枚举h的时候，倒序和正序是一样的，因为上次层m就是倒序的，所以h就算是正序，他也每次用的是上一层的，不是这一层的。如果有4层循环呢，一样，只要一层倒序即可。对于要求宠物最多的同时，体力最高。那么直接枚举就行了，找出宠物多的，如果相同那么看体力用的最少的。虽然dp的定义，没法直接求最多可以剩多少体力，但是可以求用了多少体力对吧。
第二种做法，就是以前机器人比赛做的那个金币题目。比如经典的背包体积和价值问题，只是把价值和体积的权力互换，让求的当维护的，求出来的是已知的，最后枚举判断dp里面的状态是否满足给出的限制就行。所以这题可以定义状态dp[i][j]，用了不超i的血量，捕捉了j个宠物，最少要用多少精灵球。然后最后枚举所有的状态，看看是否<精灵球的数量，如果可以就可以更新答案。同理也可以dp[i][j]定义为，用了不超过i的精灵球，捕捉了j个宠物，最少要用多少体力。然后一样的操作。
对于如何确定状态呢
就是：
1.把要求的答案，成为dp的答案，这就是最普通的做法。
2.把要求的答案，放在dp的定义状态里面，而dp的答案呢是一个已知的条件。
对于如何定义状态，就看各个限制的范围是多少，看看最少能用多少次循环，尽量选择时间复杂度最优秀的。但是一定要保证有最优子结构的前提下来处理。
还有一个值得注意的就是，一般把第一维枚举物品给优化之后，dp的状态每次就是上一层的值，所以不用考虑不选i这个物品的清空。实际上已经考虑了。但是如果用的没有优化的，那么必须就上，要不然就少更新了。必须要从1到m都要枚举，不能落下。

用了不超j的精灵球和不超k的体力,最多可以抓多少宠物。

#include<bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define db double
#define PII pair<int,int >
#define mem(a,b) memset(a,b,sizeof(a))
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
		
using namespace std;
const int mod = 1e9+7,inf = 1e9;
const int N = 2e5+10,M = 2010;

int T,n,m,k,h;
PII va[110];
int dp[1010][510];

signed main()
{
    
	IOS;
	cin>>m>>h>>n;
	for(int i=1;i<=n;i++) cin>>va[i].fi>>va[i].se;
	for(int i=1;i<=n;i++)
	{
    
		for(int j=m;j>=1;j--)
		{
    
			for(int k=1;k<=h;k++)
			{
    
				if(j>=va[i].fi&&k>=va[i].se)
				dp[j][k] = max(dp[j][k],dp[j-va[i].fi][k-va[i].se]+1);
			}
		}
	}
	int maxn = 0,sum = 0;
	for(int k=0;k<h;k++)
	{
    
		if(maxn<dp[m][k])
		{
    
			maxn = dp[m][k];
			sum = h-k;
		}
		else if(maxn==dp[m][k]) sum = max(sum,h-k);
	}
	cout<<maxn<<" "<<sum<<"\n";
	return 0;
}

用了不超j的体力和抓了k的宠物，最少用多少精灵球。

#include<bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define db double
#define PII pair<int,int >
#define mem(a,b) memset(a,b,sizeof(a))
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
		
using namespace std;
const int mod = 1e9+7,inf = 1e9;
const int N = 2e5+10,M = 2010;

int T,n,m,k,h;
PII va[110];
int dp[510][110];

signed main()
{
    
	IOS;
	cin>>m>>h>>n;
	for(int i=1;i<=n;i++) cin>>va[i].fi>>va[i].se;
	mem(dp,0x3f);
	for(int i=0;i<=h;i++) dp[i][0] = 0;
	for(int i=1;i<=n;i++)
	{
    
		for(int j=h;j>=1;j--)
		{
    
			for(int k=1;k<=n;k++)
			{
    
				if(j>=va[i].se)
				dp[j][k] = min(dp[j][k],dp[j-va[i].se][k-1]+va[i].fi);
			}
		}
	}
	int maxn = -inf,sum = 0;
	for(int i=0;i<h;i++)
	{
    
		for(int j=0;j<=n;j++)
		{
    
			if(dp[i][j]<=m)
			{
    
				if(maxn<j)
				{
    
					maxn = j;
					sum = h-i;
				}
				else if(maxn==j) sum = max(sum,h-i);
			}
		}
	}
	cout<<maxn<<" "<<sum<<"\n";
	return 0;
}

用了不超j的精灵球和抓了k的宠物，最少用多少体力。
#include<bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define db double
#define PII pair<int,int >
#define mem(a,b) memset(a,b,sizeof(a))
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
		
using namespace std;
const int mod = 1e9+7,inf = 1e9;
const int N = 2e5+10,M = 2010;

int T,n,m,k,h;
PII va[110];
int dp[1010][110];

signed main()
{
    
	IOS;
	cin>>m>>h>>n;
	for(int i=1;i<=n;i++) cin>>va[i].fi>>va[i].se;
	mem(dp,0x3f);
	for(int i=0;i<=m;i++) dp[i][0] = 0;
	for(int i=1;i<=n;i++)
	{
    
		for(int j=m;j>=1;j--)
		{
    
			for(int k=1;k<=n;k++)
			{
    
				if(j>=va[i].fi)
				dp[j][k] = min(dp[j][k],dp[j-va[i].fi][k-1]+va[i].se);
			}
		}
	}
	int maxn = -inf,sum = 0;
	for(int i=0;i<=m;i++)
	{
    
		for(int j=0;j<=n;j++)
		{
    
			if(dp[i][j]<h)
			{
    
				if(maxn<j)
				{
    
					maxn = j;
					sum = h-dp[i][j];
				}
				else if(maxn==j) sum = max(sum,h-dp[i][j]);
			}
		}
	}
	cout<<maxn<<" "<<sum<<"\n";
	return 0;
}

机器人的金币题目: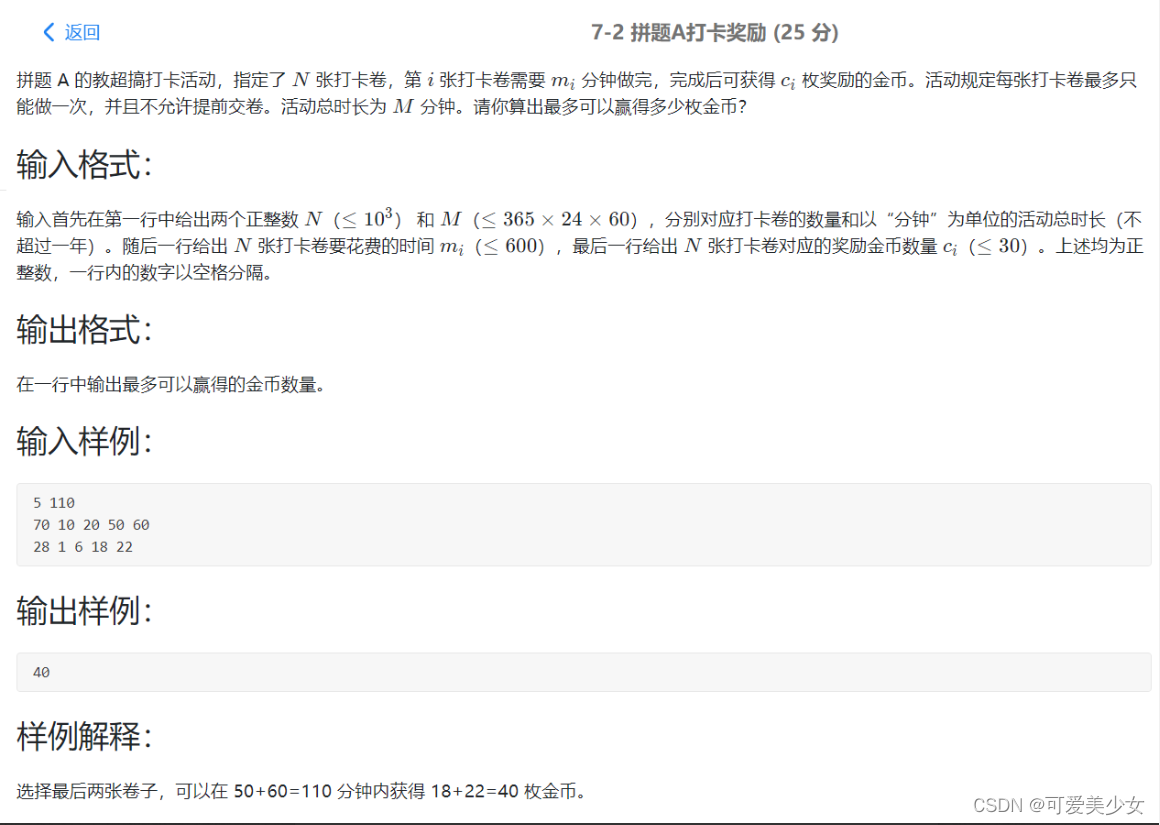

思考：
要是按正常的思路就是dp[i][j]用了前i个卡卷，不超过j的时间，最多可以得到多少金币。但是这样两重循环肯定超时了。但是发现金币的范围就很小。所以dp[i][j]定义为用了前i个卡卷，得到不超过j的金币，最少用多少时间。最后金币这个答案枚举一下就行了，在保证时间不超条件的前提下。

代码：

二维版本：

#include<bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define db double
#define int long long
#define PII pair<int,int >
#define mem(a,b) memset(a,b,sizeof(a))
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
		
using namespace std;
const int mod = 1e9+7,inf = 1e18;
const int N = 2e5+10,M = 2010;

int T,n,m,k;
PII va[N];
int dp[1010][30010];

signed main()
{
    
	IOS;
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>va[i].fi;
	for(int i=1;i<=n;i++) cin>>va[i].se;
	int R = n*30;
	mem(dp,0x3f);
	for(int i=0;i<=n;i++) dp[i][0] = 0;
	for(int i=1;i<=n;i++)
	{
    
		for(int j=1;j<=R;j++)
		{
    
			dp[i][j] = min(dp[i][j],dp[i-1][j]); //注意这里是两重循环的时候不能丢掉，如果优化一重循环，那么本身就已经是上一层的了，所以不用再写了，但是这里都要更新。必须要从1到R，不能从va[i].se开始，因为那样就少了。
			if(j>=va[i].se)
			dp[i][j] = min(dp[i][j],dp[i-1][j-va[i].se]+va[i].fi);
		}
	}
	int maxn = 0;
	for(int i=1;i<=R;i++)
	{
    
		if(dp[n][i]<=m)
		maxn = max(maxn,i);
	}
	cout<<maxn;
	return 0;
}

一维版本：
#include<bits/stdc++.h>
#define fi first
#define se second
#define pb push_back
#define db double
#define int long long
#define PII pair<int,int >
#define mem(a,b) memset(a,b,sizeof(a))
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
		
using namespace std;
const int mod = 1e9+7,inf = 1e18;
const int N = 2e5+10,M = 2010;

int T,n,m,k;
PII va[N];
int dp[30010];

signed main()
{
    
	IOS;
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>va[i].fi;
	for(int i=1;i<=n;i++) cin>>va[i].se;
	int R = n*30;
	mem(dp,0x3f);
	dp[0] = 0;
	for(int i=1;i<=n;i++)
	{
    
		for(int j=R;j>=va[i].se;j--) //因为dp本身就是上一层的，所以这里从va[i].se开始没事。
		dp[j] = min(dp[j],dp[j-va[i].se]+va[i].fi);
	}
	int maxn = 0;
	for(int i=1;i<=R;i++)
	{
    
		if(dp[i]<=m)
		maxn = max(maxn,i);
	}
	cout<<maxn;
	return 0;
}

总结：
多多思考呀，理解算法的的本质。