当前位置:网站首页>Daily Practice:Codeforces Round #794 (Div. 2)(A~D)
Daily Practice:Codeforces Round #794 (Div. 2)(A~D)
2022-07-05 07:20:00 【_dawn°】
VP*n,,主要是这场cf时间太阴间了hhhhh
A. Everything Everywhere All But One

给出n个数,选择n-1个数,并用这些数的平均数代替这些数的每一个数, 问是否能通过若干次操作使得数组中的数都相等。
思路:既然要选择n-1个数改为平均数,那就要满足这n-1个数的平均数是整个数组的平均数,且未选择的那个数是这个平均数。注意使用double保精度。
A Code:
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=55;
int t,n;
double a[N];
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin>>t;
while(t--){
std::cin>>n;
double sum=0;
std::map<double,int>mp;
for(int i=1;i<=n;i++){
std::cin>>a[i];
mp[a[i]]++;
sum+=a[i];
}
std::cout<<(mp[sum/n]?"YES":"NO")<<'\n';
}
return 0;
}B. Odd Subarrays

给出数组,问怎样切分数组,使得尽可能多的子数组逆序对为奇数。
思路:贪心,既然是满足逆序对为奇数,那只要存在一个逆序对,那就划分开即可。
AC Code:
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=1e5+5;
int t,n;
int a[N];
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin>>t;
while(t--){
std::cin>>n;
for(int i=1;i<=n;i++){
std::cin>>a[i];
}
int ans=0;
for(int i=1;i<n;i++){
if(a[i]>a[i+1]) ans++,i++;
}
std::cout<<ans<<'\n';
}
return 0;
}os:一开始因为数组开小了T了一发,气死QWQ
C. Circular Local MiniMax

给出一个数列,是否可以通过对数组内元素的重新排列使得它满足:首尾相连后,任意一个元素都满足大于相邻两数或小于相邻两数。
思路:首先,数组元素个数为奇数时,是无法构造的;然后把数组排序,分成前后两部分,一大一小交叉摆放,最后判断满足条件即可。
AC Code:
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=1e5+5;
int t,n;
int a[N],ans[N];
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin>>t;
while(t--){
std::cin>>n;
memset(ans,0,sizeof(ans));
int cnt=0;
for(int i=1;i<=n;i++){
std::cin>>a[i];
}
if(n&1){
std::cout<<"NO"<<'\n';
continue;
}
std::sort(a+1,a+1+n);
std::vector<int>vecs,vecl;
for(int i=1;i<=n/2;i++){
vecs.push_back(a[i]);
}
for(int i=n/2+1;i<=n;i++){
vecl.push_back(a[i]);
}
for(int i=0;i<n/2;i++){
ans[++cnt]=vecs[i];
ans[++cnt]=vecl[i];
}
bool flag=true;
ans[0]=ans[cnt];
ans[++cnt]=ans[1];
for(int i=1;i<=n;i++){
if(!(ans[i]>ans[i+1]&&ans[i]>ans[i-1]||ans[i]<ans[i+1]&&ans[i]<ans[i-1])){
flag=false;
break;
}
}
if(!flag){
std::cout<<"NO"<<'\n';
continue;
}
std::cout<<"YES"<<'\n';
for(int i=1;i<=n;i++){
std::cout<<ans[i]<<" \n"[i==n];
}
}
return 0;
}os:很意外,这次的C不难欸
D. Linguistics

给出A,B,AB,BA四种元素的个数,给出字符串s,判断用给出的元素是否可以组成该字符串。
思路:学习大佬的思路!(这个佬居然是现场打的这场cf,tqlllllll)
首先若是给出的元素中A和B的个数不符合,那一定不可能;数据范围很大,我们没法直接枚举,那我们可以采用这种思想:找到最小需要各个种类元素的个数,分别比较即可。
我们先用双指针截取类似ABAB,BABA这样相互之间不相同的子串。对于A和AB,我们可以一起算出最小需要数量,而B和BA是一样的计算方法。
长度为偶数的这种子串只有两种,即ABAB和BABA,对于BABA这样的,可以不需要AB元素,而ABAB可以通过减少一对单独的A和B来变成BABA类似子串。单是若是没有一对单独的A和B,那就需要len/2个AB,那我们就可以使用成对的单独的A和B来尽可能减少AB的用量,算出AB最少的用量。而对于奇数长度的子串,我们可以减少A或B使它变成上述两种子串,采用相同的处理方法。
AC Code:
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long ll;
const int mod=1e9+7;
const int N=1e5+5;
int T;
int a[6];
std::string s;
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
std::cin>>T;
while(T--){
for(int i=1;i<=4;i++){
std::cin>>a[i];
}
std::cin>>s;
int cntA=0,cntB=0;
int len=s.length();
for(int i=0;i<len;i++){
if(s[i]=='A') cntA++;
else cntB++;
}
if(!(cntA==a[1]+a[3]+a[4]&&cntB==a[2]+a[3]+a[4])){
std::cout<<"NO"<<'\n';
continue;
}
int cntab=0,cntba=0;
std::vector<int>ab,ba;
for(int i=0;i<len;i++){
int j=i;
while(j+1<len&&s[j+1]!=s[j]) j++;
if(j-i+1&1){
if(s[i]=='A') a[1]--;
else a[2]--;
}
else{
int t=j-i+1>>1;
if(s[i]=='A') ab.push_back(t),cntab+=t;
else ba.push_back(t),cntba+=t;
}
i=j;
}
if(a[1]<0||a[2]<0){
std::cout<<"NO"<<'\n';
continue;
}
int t=std::min(a[1],a[2]);
std::sort(ab.begin(),ab.end());
while(!ab.empty()&&t){
t--;
cntab-=ab.back();
ab.pop_back();
}
if(cntab>a[3]){
std::cout<<"NO"<<'\n';
continue;
}
t=std::min(a[1],a[2]);
std::sort(ba.begin(),ba.end());
while(!ba.empty()&&t){
t--;
cntba-=ba.back();
ba.pop_back();
}
if(cntba>a[4]){
std::cout<<"NO"<<'\n';
continue;
}
std::cout<<"YES"<<'\n';
}
return 0;
}os:这个D感觉还是很难想的,,看佬的思路都要理解好久
若有错误请指教,谢谢!
边栏推荐
- PHY drive commissioning - phy controller drive (II)
- PHY drive commissioning --- mdio/mdc interface Clause 22 and 45 (I)
- 2022.06.27_ One question per day
- Energy conservation and creating energy gap
- HDU1231 最大连续子序列(分治or动规or双指针)
- Matlab在线性代数中的应用(四):相似矩阵及二次型
- Altimeter data knowledge point 2
- C#学习笔记
- NPM and package common commands
- Docker installs MySQL and uses Navicat to connect
猜你喜欢

【无标题】

Mathematical analysis_ Notes_ Chapter 8: multiple integral
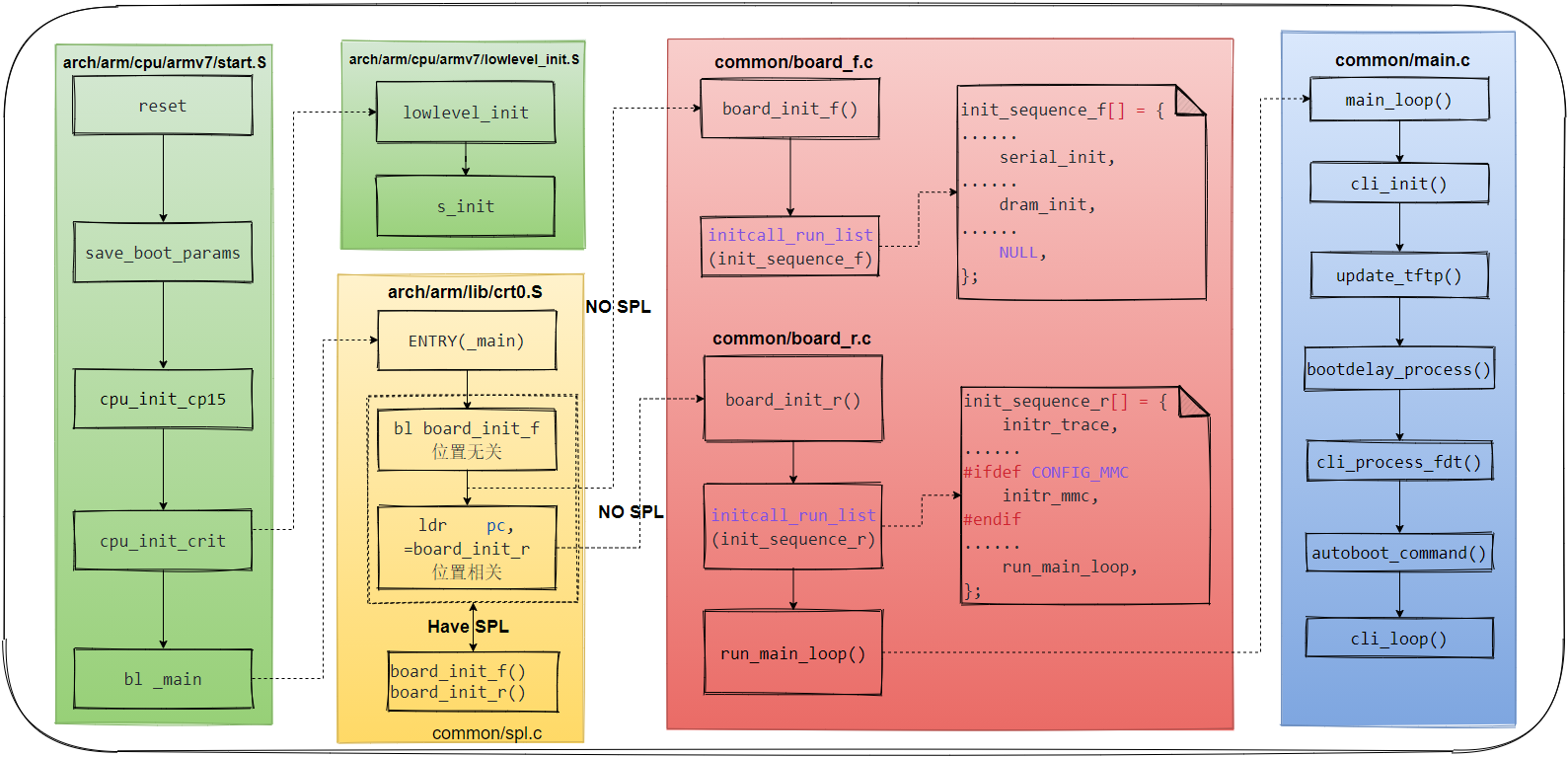
U-boot initialization and workflow analysis

Docker installs MySQL and uses Navicat to connect
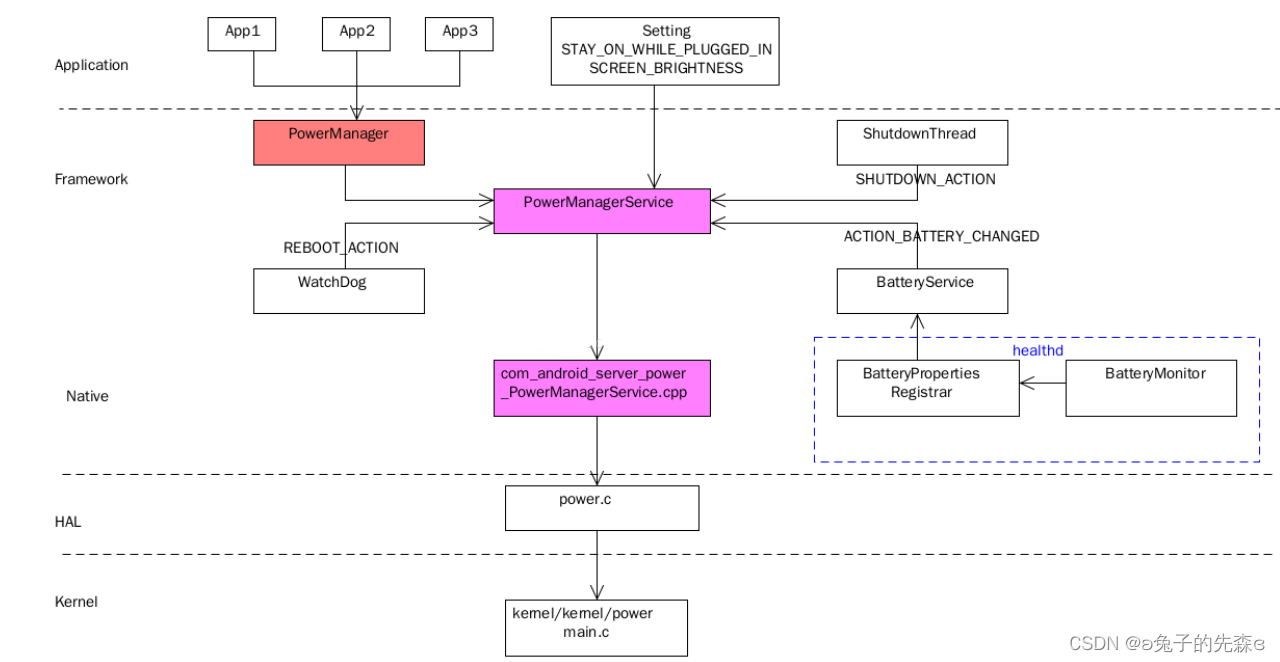
Powermanagerservice (I) - initialization

PowerManagerService(一)— 初始化

docker安装mysql并使用navicat连接
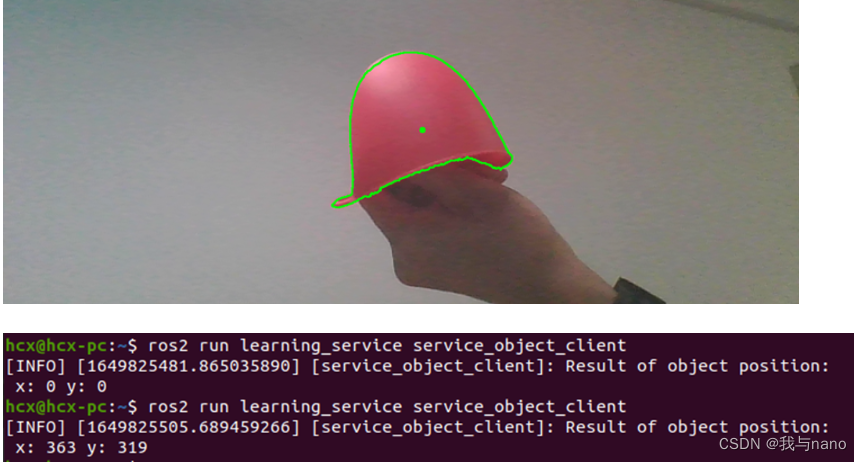
Ros2 - Service Service (IX)
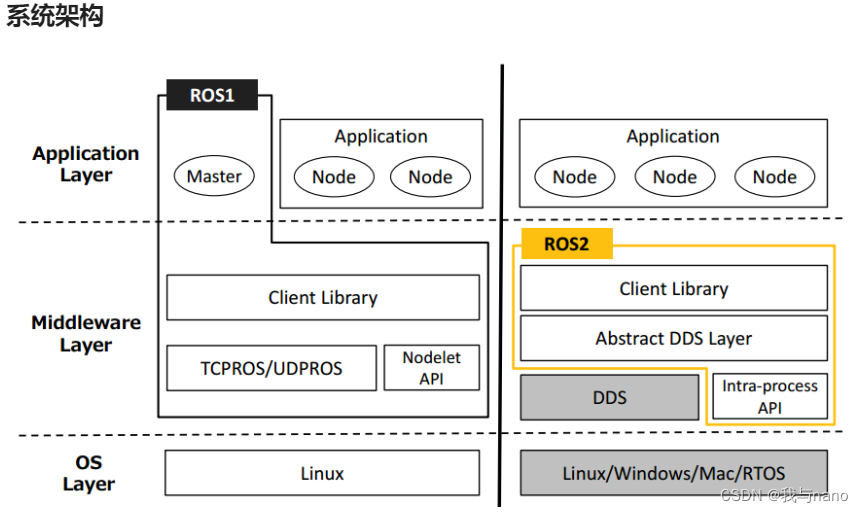
Ros2 - ros2 vs. ros1 (II)

Using GEE plug-in in QGIS
随机推荐
Logical structure and physical structure
How can Oracle SQL statements modify fields that are not allowed to be null to allow nulls?
Ros2 - common command line (IV)
SD_ CMD_ SEND_ SHIFT_ REGISTER
What does soda ash do?
Energy conservation and creating energy gap
Ugnx12.0 initialization crash, initialization error (-15)
NPM and package common commands
网易To B,柔外刚中
HDU1232 畅通工程(并查集)
The difference between NPM install -g/-save/-save-dev
window navicat连接阿里云服务器mysql步骤及常见问题
【Node】npm、yarn、pnpm 区别
Brief description of inux camera (Mipi interface)
Mid 2022 documentary -- the experience of an ordinary person
When jupyter notebook is encountered, erroe appears in the name and is not output after running, but an empty line of code is added downward, and [] is empty
What is sodium hydroxide?
目标检测系列——Faster R-CNN原理详解
Unity ugui how to match and transform coordinates between different UI panels or uis
And play the little chestnut of dynamic agent