Set theory of Discrete Mathematics (I)

Set theory of Discrete Mathematics

Books used

《 Discrete mathematics and its applications 》（ The first 3 edition ） Edited by Fu Yan and others .

The purpose of writing

In order to record the process of learning discrete mathematics . Write down your understanding of Discrete Mathematics , It's more interesting to record while learning . Limited personal level , There are some mistakes in the article , You can point out . Then I mainly write what I understand , Just take it with you from the textbook , If you write down what is in the textbook , Then you might as well read the textbook directly .

aggregate

The English word is set. I have known Jiji since high school , At that time, set learning was relatively simple , Now it's University , Relearn this set . It doesn't make much difference .

Concept

Textbook ：

• Set is a basic mathematical concept that cannot be defined accurately
• A set is made up of all objects in a specified range that meet a given condition

I understand ：

A set is a mathematical container , The elements with common properties are stored in the container . The elements can be numbers or other objects .

Example ：

The containers encountered later are all collections , in my opinion , A collection is a container , But containers are not necessarily collections . After all, I have studied data structure , There are many containers besides collections , For example, linked list , Array , Stack , Line up, etc , These are containers .

1） All leather sofas in China

• Now there is a container , This container stores the sofa , The nature of this sofa is （ China's , be-all , Leather ）, The intersection of the three properties forms the property of the sofa in the current container

2） All the seagulls

• Now there is a container , This container holds seagulls , The nature of this seagull is （ be-all ）, That is, as long as an object is a seagull , Then this object is contained in this container

3） stay -1 and 1 All rational numbers between

• Understand one ： Now there is a container , This container holds rational numbers , The property of this rational number is （ All in -1 To 1 In the interval of ）, Rational numbers satisfying this property can be placed in the same set （ Containers ）.
• Understanding two ： Now there is a container , This container holds numbers , The property of this number is （ All in -1 To 1 Go to in the interval , Reasonable ）, Numbers satisfying this property can be placed in the same set （ Containers ）

4） All Asians

• Now there is a container , This container is for people , The nature of this kind of person is （ All of you , Asian ）, People who satisfy these two properties at the same time can be stored in a set .

5） All courses offered by Chinese colleges and universities

• Now there is a container , This container holds courses , The nature of this course is （ China's , College , Opened , be-all ）. Courses that meet the intersection of these properties can be stored in a container .

6） All the street lights and trees in Tiananmen Square

• Now there are two objects , One is street lamp , One is a tree , So there is a ” or “ The relationship between , That is to say, there is a big container , Inside the big container are two small containers , One container holds , All the street lights in Tiananmen Square ; Another container holds all the trees in Tiananmen Square . Then the union of these two small containers is the big container .

7） all C Identifier in language

• Now there is a container , This container stores identifiers , The nature of this identifier is （C Linguistic , be-all ）,C The nature of language identifiers （ The combination of English letters, numbers and underscores , Can 't start with a number , It cannot be predefined by the system ）, Identifiers that meet these conditions can be placed in the same container .

8） All prime numbers

• Now there is a container , This container holds numbers , The nature of this number is （ All of you , The satisfaction factor is only 1 And ）, Numbers that meet this nature can be placed in a container .

There are two more examples , And the 8 Almost .

Each object in the specified range is called the Elements

Generally, English capital letters are used to represent sets , Use English letters in lowercase to represent elements .

Basic properties of sets

I learned this in high school , If you forget, it will be regarded as review , Sets have three basic properties ：

• deterministic
• The opposite sex
• Disorder

Certainty means , The elements in the set must be definite , You can't put an uncertain thing in a set .

What opposites say is , The elements in the set do not repeat , If it repeats, just keep one of them , Delete the others .

Disorder means , There is no order requirement for the elements in the set , Numbers can be ranked from large to small , You can also go from small to large , Or put it in a mess , It's OK , No problem at all . The same is true for non digital ones , Put it as you like , Just let it go anyway .

The representation of a set

There are many ways to represent a set ： The textbook introduces 5 Kind of ：

• Enumeration
• Narrative
• Induction
• Recursively specify the set method
• Venn's graphic method

Enumeration

Enumeration method is also called display method . The meaning is obvious , Just directly Violence enumeration , If you can know the appearance of all elements in the set, list them one by one . If you only know a part , Then write a few and see what rules they have , Then write and use directly according to the rules … It indicates that the elements in the current set have such a rule .

Example ：

1）A={a,b,c,d};

• Because of the collection A There is only 4 Elements , Elements are alphabetic , And we know what letters look like , Then you can list them directly .

2）B={2,4,6,8,…,2n,…};

• Because of the collection B We can know the law of the elements in , I don't know how many . Then you can use ellipsis to list , Tell the viewer , My set is even , Every element is 2 Multiple .

From a computer perspective , Display method is a kind of ” static state “ notation . Static means more memory , The memory of stack area is limited , The current heap memory is also limited , But the memory of heap area is many times larger than that of stack area .

Narrative

The method of representing a set by characterizing some characteristics of the elements in the set is called narration Law .

Narrative method is also called implicit method .

To put it simply ： Narrative method is to describe the elements in the set , Elements that meet this description belong to this set .

From the definition , Use narration to express the writing method of set ：

Collection name ={ Elements | Description of elements }

Example ：

1）M={m|m Is beauty }

• That means , If m Is beauty m It belongs to the set M. If m If it's not beauty, it doesn't belong to the collection M. A little more vernacular . Now it is stipulated that Alice Is beauty ,Jack It's a handsome guy . Then put the Alice Plug in m, It becomes Alice Is beauty , Satisfy , therefore Alice Belong to a collection M. hold Jack Plug in m, It becomes Jack Is beauty , dissatisfaction , Because it has been stipulated above Jacke It's a handsome guy , therefore Jack Definitely not a beauty , therefore Jack It doesn't belong to a collection M.

2）A={x|x yes discrete mathematics All the letters in }

• According to the mutuality of the set, we get the set A={d,i,s,c,r,e,t,m,a,h}. Then substitute elements from the outside x, If x yes r, that x It belongs to the set A, If x yes p, that x It doesn't belong to the set A. Because in the collection A in r It belongs to A Of , and p Do not belong to A.

3）Z={x|x It's an integer }

• As in the first example , From the outside , Now it is stipulated that y=8, hold y Plug in x, That's judgment y Is it an integer , If it is , be y Belong to a collection Z. If not , be y It doesn't belong to a collection Z. Obviously y=8,8 Is an integer , therefore y Belong to a collection Z.

the previous C The language code ：

#include <stdio.h>

int isInt(double y)
{
    
    int a=(double)y;	// Truncate the integral part 
    return y-a?0:1;		// Subtract its integer part from the original number , If there is remainder, it is not an integer , If there is no remainder, it is an integer 
}

int main()
{
    
    double y;
    printf(" Please enter an integer ");
    scanf("%lf",&y);
    if(isInt(y))
        printf("%f Is an integer ",y);
    else
        printf("%f Is not an integer ",y);
    return 0;
}

The characteristic of narrative method is that the elements of the set represented can be many or infinite , And from a computer perspective , Narration is a kind of ” dynamic “ Representation , When the computer processes data, it does not need to occupy a large amount of memory in the stack .

Induction

Induction is a method of defining sets only by induction , It mainly consists of the following three parts ：

• Basics , Point out that some of the most basic elements belong to sets
• inductive , Point out the method of constructing new elements from basic elements
• Minimalism , Indicate the bounds of the set

The first and second parts point out the elements that a set must contain at least , The third part points out the elements that a set contains at most .

After reading the textbook more , My understanding is that , After the first and second parts determine what the element looks like , And then keep combining these large and small elements in a loop , Then we get that the final set is composed of oneortwo elements from the beginning , To multiple elements combined .

You used to have only 0 and 1, Then combine once to form new elements 00,01,10,11,000,001,010,100 etc. . Then to the third part, the final set structure is {0,1,00,10,01,11,000,001,010,100,011,110,111,0000,0001,…,…}. Like this . I don't know whether this part is right , If you are wrong, help correct it .

Recursively specify the set method

Recursively specifying the set method refers to the method of defining the elements in the set through calculation rules

In short, it's , After determining the previous elements , There is a specific relationship between the following elements and the previous elements , Keep going back , In short, there is a set representation of a special relationship between the front and back

Example ：

a(0)=1,a(1)=2*a(0),a(2)=2*a(1),…a(n)=2*a(n-1),n>1,S={a(0),a(1),a(2),…,}; Try to write a set S All elements of . In fact, it is impossible to finish writing , It can only be displayed by enumerating . Set according to the law of the sequence S={1,2,4,8,…,2^n,…} (n>=0)

Venn's graphic method

It's the Wayne diagram learned in high school . Is to regionalize the set , Use graphic description . Generally, square and oval paintings are used , Then there are small sets in large sets. This type of representation is Wen's diagram .

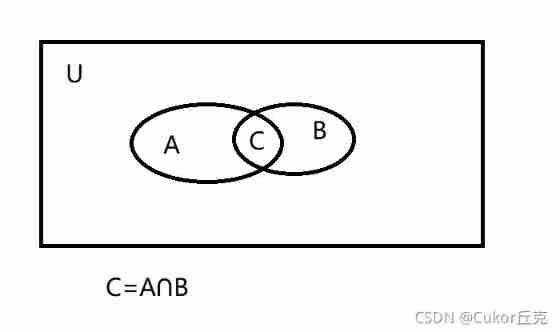
The relationship between sets and elements

Between elements and collections ” Belong to “ The relationship is ” Definite “.

For a set A And elements a Come on , Only a Belong to A, perhaps a Do not belong to A, Two statements .

• a Belong to A Write it down as ：a∈A

• a Do not belong to A Write it down as ：a∉A

In Discrete Mathematics , Just be clear about the boundaries 、 No ambiguous description for discussion , And the set constructed by the unclear pair belongs to Fuzzy set theory The research scope of .

The relationship between sets

Equality relation ： If the elements of two sets are the same , Then these two sets are equal .

The relationship between inclusion and inclusion ： If the collection A Elements in the collection B Can be found in , Then it indicates that the set A Is a collection B Subset . This time is B contain A Or say A Included in B. stay B contain A Under the premise of , If A It doesn't contain B, shows A yes B Subset , but B No A Subset ; If A contain B, shows A and B Contain each other , Then these two sets are equal .

True subset ： set up A,B Is an arbitrary set , If A contain B, also A It's not equal to B, be B yes A The proper subset of .

Several special sets

An empty set ：

A set without any elements is called an empty set . Write it down as ∅

Empty sets exist objectively

Example ：

set up A={x|x∈R And x^2<0}

Because in the range of real numbers ,x The square of must be greater than or equal to zero , Not less than zero , So assemble A For an empty set .

Theorem ：

• An empty set is a subset of all sets
• Empty sets are unique

The complete ：

In a relatively fixed range , A collection containing all elements in this range , Called a set .

Theorem ：

The complete set is relatively unique

Because the original meaning of the complete set is the meaning of all inclusion , But the scope of the complete set is artificially prescribed , You say the earth is a complete collection , What is the whole galaxy ？ If you say the galaxy is a complete collection , What is the whole universe ？ There is more space outside the universe . By analogy . So the complete works are relatively .

base ：

aggregate A The number of elements in is called the cardinality of the set , Write it down as |A|

That's easy to understand , It is equivalent to the length of the array . How many elements in the collection | Collection name | Just how much .

public class Demo{
    
    public static void main(String[] args){
    
        int[] arr={
    5,2,4,63,4,6};		// Yes 6 Elements 
        System.out.println(arr.length);	// Output 6
    }
}

If the cardinality of a set is finite , Then the set is called a finite set .

If the cardinality of a set is infinite , The set is said to be infinite .

Example ：

1）A=∅;

• |A|=0, Because an empty set is a set that contains no elements , So the cardinality of an empty set is zero , therefore A The cardinality of is zero .

2）B={∅};

• |B|=1, because B A set is an element that contains an empty set , therefore B Based on 1.

Pay attention to these two questions , Very important concept , The idea should be reasonable .

3）C={a,b,c};

• |C|=3, because C There are three elements

4）D={a,{b,c}};

• |D|=2, From the back {b,c} It can be inferred that , aggregate D The stored elements are collections . therefore a It is also regarded as a collection , therefore D Based on 2

Definition ：

If a collection A contain n Elements , It's called a collection A by n Meta set , call A Contains m Elements （m<=n） Subset of is its m Meta subset .

set up A For any set , Assemble A The set of all the different subsets of is called A Power set of .

Symbolization ：P（A）={x|x⊆A}

Example ：

1）P（∅）

• p（∅）={∅}, Because empty sets have no subsets

2）p（{∅}）

• p（∅）={∅,{∅}}, because {∅} Is also a containing ∅ Set , Its cardinality is 1, Its subset is empty , and {∅} Itself is also p（∅） Subset , therefore p（∅） The power set of is obvious .

3）p（a,{b,c}）

• p(a,{b,c})={ {a},{b},{c},{b,c},{a,{b,c}}}, Take the inside apart .a become {a};{b,c} It can be disassembled into {b},{c}; And finally get up , Remember to add the split subset itself .

Cukor Chuck homepage , Welcome to ！！！