当前位置:网站首页>Binary search (half search)
Binary search (half search)
2022-07-05 07:01:00 【rockvine】
List of articles
One 、 Algorithm interpretation
Two points search It's often called Dichotomy perhaps Binary search , During each search, the search is continued by dividing the interval to be searched into two parts and taking only one part , Greatly reduce the complexity of searching . For a length of O(n) Array of , The time of binary search The impurity is O(log n).
for instance , Given an ordered array {3, 4, 5, 6, 7}, We want to find 4 Not in this array . Consider the median when halving for the first time 5, because 5 Greater than 4 , So if 4 Exists in this array , Then it must exist in 5 This one on the left And a half . So our search interval becomes {3, 4, 5}.( Be careful , According to the specific situation and your problem brushing habits , there 5 You can keep it or not , Does not affect the level of time complexity ). Consider the new median for the second half 4, Just the number we need to find . So we found that , For a length of 5 Array of , We just did 2 Search times . If it's traversing arrays , In the worst case, you need to find 5 Time .
We can also define binary search in a more mathematical way . Given one in [a, b] Monotone function in interval f(x), if f(a) and f(b) Opposite positive and negative , Then there must be a solution c, bring f(c) = 0. In the last example ,f(x) Is a discrete function f(x) = x + 2, lookup 4 Whether there is an equivalent to seeking f(x) - 4 = 0 Whether there is a discrete solution . because f(1) - 4 = 3 - 4 = -1 < 0,f(5) - 4 = 7 - 4 = 3 > 0, And the function increases monotonically in the interval , Therefore, we can use binary search to solve . If the last two points can't be divided again , If there is only one number left , And there is no solution satisfying the condition in the remaining interval , Then there is no discrete solution , namely 4 Not in this array .
Specific to the code , Binary search between the left and right end of the time zone, take the open interval or closed interval, in most cases , Therefore, it is sometimes easy to be confused about how to define interval openness . Here are two tips , The first is to try to use a writing method skillfully , For example, close left and open right ( Meet the habit of programming ) Or close left and right ( Easy to handle boundary conditions ), Try to keep this one way of writing ; The second is to think about when brushing questions. If there is only one or two numbers left in the last interval , Whether your writing will fall into a dead circle , If some kind of writing can't jump out of the dead circle , Then consider trying another way of writing .
Binary search can also be seen as a special case of double pointers , But we usually distinguish between the two . Two pointer questions , The pointer usually moves step by step , And in binary search , The pointer moves half an interval at a time .
Two 、 Ask for directions
2.1、x The square root of
2.1.1、 Title Description
69. x The square root of
Give you a nonnegative integerx, Calculate and returnxOf Arithmetical square root .
Because the return type is an integer , Results are retained only Integral part , The decimal part will be Give up .
Be careful : No built-in exponential functions and operators are allowed , for examplepow(x, 0.5)perhapsx ** 0.5.
2.1.2、 I / O example
Example 1:
Input : x = 4
Output : 2
Example 2:
Input : x = 8
Output : 2
explain : 8 The arithmetic square root of is 2.82842…, Because the return type is an integer , The decimal part will be removed .
2.1.3、 Answer key
The lower bound of binary search is 0, The upper bound can be roughly set to x. In each step of binary search , We just need to compare the intermediate elements mid The sum of the squares of x The size of the relationship , The range of the upper and lower bounds is adjusted by comparing the results .
class Solution {
public int mySqrt(int x) {
int left = 0, right = x, ans = -1;
while (left <= right) {
int mid = left + (right - left) / 2;
if ((long) mid * mid <= x) {
ans = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return ans;
}
}
Complexity analysis
- Time complexity :O(logx), That is, the number of times needed for binary search .
- Spatial complexity :O(1).
3、 ... and 、 Search interval
3.1、 Find the first and last positions of the elements in the sort array
3.1.1、 Title Description
34. Find the first and last positions of the elements in the sort array
Give you an array of integers in non decreasing ordernums, And a target valuetarget. Please find out the start position and end position of the given target value in the array .
If the target value does not exist in the arraytarget, return[-1, -1].
You must design and implement a time complexity ofO(log n)The algorithm to solve this problem .
3.1.2、 I / O example
Example 1:
Input : nums = [5, 7, 7, 8, 8, 10], target = 8
Output : [3,4]
Example 2:
Input : nums = [5, 7, 7, 8, 8, 10], target = 6
Output : [-1,-1]
Example 3:
Input : nums = [], target = 0
Output : [-1,-1]
3.1.3、 Answer key
Four 、 Select array to find numbers
4.1、 Search rotation sort array II
4.1.1、 Title Description
81. Search rotation sort array II
It is known that there is an array of integers in non descending ordernums, The values in the array don't have to be different from each other .
Before passing it to a function ,numsIn some unknown subscriptk(0 <= k < nums.length) On the rotate , Make array[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]( Subscript from 0 Start Count ). for example ,[0,1,2,4,4,4,5,6,6,7]In subscript 5 It may turn into[4,5,6,6,7,0,1,2,4,4].
Here you are. After rotation Array ofnumsAnd an integertarget, Please write a function to determine whether the given target value exists in the array . IfnumsThere is a target value intarget, Then return totrue, Otherwise return tofalse.
You must minimize the whole procedure .
4.1.2、 I / O example
Example 1:
Input : nums = [2, 5, 6, 0, 0, 1, 2], target = 0
Output : true
Example 2:
Input : nums = [2, 5, 6, 0, 0, 1, 2], target = 3
Output : false
4.1.3、 Answer key
5、 ... and 、 practice
5.1、 Basic difficulty
5.1.1、 Look for the minimum value in the rotation sort array II
5.1.1.1、 Title Description
Look for the minimum value in the rotation sort array II
We know a length ofnArray of , In ascending order in advance , Through1TonTime rotate after , Get the input array . for example , Original arraynums = [0,1,4,4,5,6,7]After the change may get :
- If you rotate 4 Time , You can get [4,5,6,7,0,1,4]
- If you rotate 7 Time , You can get [0,1,4,4,5,6,7]
Be careful , Array
[a[0], a[1], a[2], ..., a[n-1]]Rotate once The result is an array[a[n-1], a[0], a[1], a[2], ..., a[n-2]].
Give you a chance to exist repeat An array of element valuesnums, It turns out to be an ascending array , According to the above situation, we have made many rotations . Please find and return the The smallest element .
You must minimize the steps of the whole process .
5.1.1.2、 I / O example
Example 1:
Input : nums = [1, 3, 5]
Output : 1
Example 1:
Input : nums = [2, 2, 2, 0, 1]
Output : 0
5.1.1.3、 Answer key
5.1.2、 A single element in an ordered array
5.1.2.1、 Title Description
A single element in an ordered array
Give you an ordered array of integers only , Each of these elements will appear twice , Only one number will appear once .
Please find and return the number that only appears once .
The solution you design must meetO(log n)Time complexity andO(1)Spatial complexity .
5.1.2.2、 I / O example
Example 1:
Input : nums = [1, 1, 2, 3, 3, 4, 4, 8, 8]
Output : 2
Example 1:
Input : nums = [3, 3, 7, 7, 10, 11, 11]
Output : 10
5.1.2.3、 Answer key
5.2、 Advanced difficulty
5.2.1、 Find the median of two positive arrays
5.2.1.1、 Title Description
Find the median of two positive arrays
Given two sizes, they aremandnPositive order of ( From small to large ) Arraynums1andnums2. Please find and return the values of these two positive ordered arrays Median .
The time complexity of the algorithm should beO(log (m+n)).
5.2.1.2、 I / O example
Example 1:
Input : nums1 = [1, 3], nums2 = [2]
Output : 2.00000
explain : Merge array = [1, 2, 3] , Median 2
Example 1:
Input : nums1 = [1, 2], nums2 = [3, 4]
Output : 2.50000
explain : Merge array = [1, 2, 3, 4] , Median (2 + 3) / 2 = 2.5
5.2.1.3、 Answer key
边栏推荐
- . Net core stepping on the pit practice
- SRE核心体系了解
- The “mode“ argument must be integer. Received an instance of Object
- PowerManagerService(一)— 初始化
- Sum of two numbers, the numbers in the array are converted to decimal, added, and output inversely
- iNFTnews | 喝茶送虚拟股票?浅析奈雪的茶“发币”
- 数学分析_笔记_第8章:重积分
- 【obs】x264编码:“buffer_size“
- Pycahrm reports an error: indentation error: unindent does not match any outer indentation
- Cloud native related technology learning
猜你喜欢
Marvell 88E1515 PHY loopback模式测试
Ret2xx---- common CTF template proposition in PWN
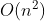
Rehabilitation type force deduction brush question notes D1
Build a microservice cluster environment locally and learn to deploy automatically
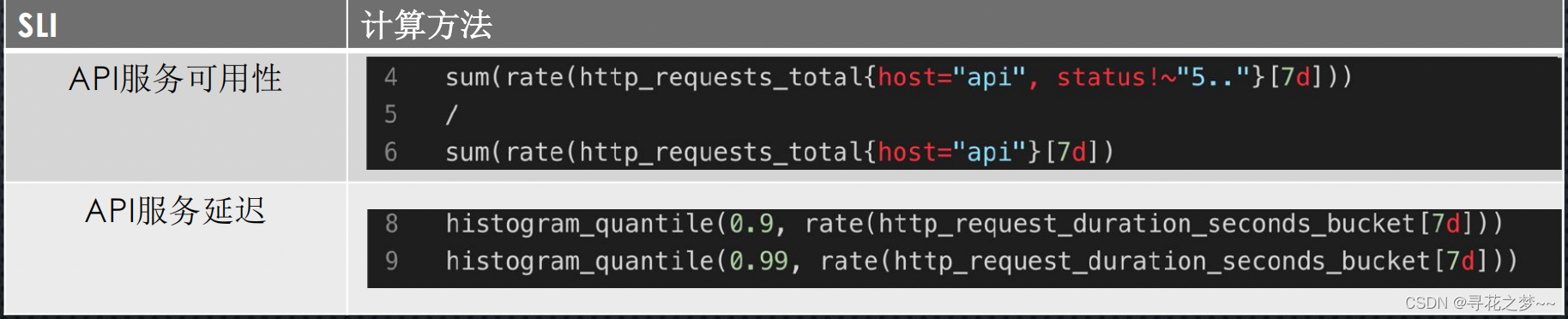
SRE核心体系了解
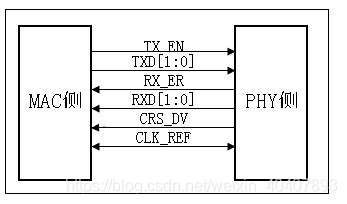
Literacy Ethernet MII interface types Daquan MII, RMII, smii, gmii, rgmii, sgmii, XGMII, XAUI, rxaui
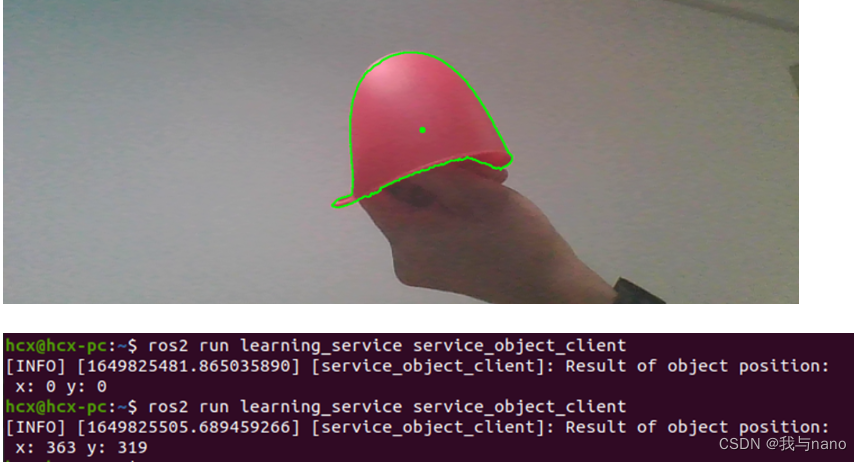
Ros2 - Service Service (IX)

SD_CMD_SEND_SHIFT_REGISTER

MySQL (UDF authorization)
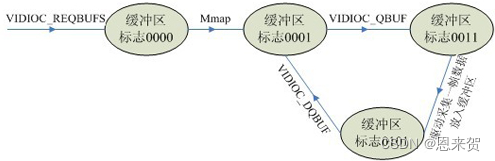
inux摄像头(mipi接口)简要说明
随机推荐
Configuration method and configuration file of SolidWorks GB profile library
LSA Type Explanation - detailed explanation of lsa-2 (type II LSA network LSA) and lsa-3 (type III LSA network Summary LSA)
数据库Mysql全部
Ros2 - first acquaintance with ros2 (I)
PR automatically moves forward after deleting clips
npm install -g/--save/--save-dev的区别
PHY驱动调试之 --- PHY控制器驱动(二)
【obs】x264编码:“buffer_size“
Volcano 资源预留特性
SD_CMD_RECEIVE_SHIFT_REGISTER
IPage能正常显示数据,但是total一直等于0
Huawei bracelet, how to add medicine reminder?
PHY drive commissioning --- mdio/mdc interface Clause 22 and 45 (I)
window navicat连接阿里云服务器mysql步骤及常见问题
PHY drive commissioning - phy controller drive (II)
网易To B,柔外刚中
PHY驱动调试之 --- MDIO/MDC接口22号和45号条款(一)
Build a microservice cluster environment locally and learn to deploy automatically
基于FPGA的一维卷积神经网络CNN的实现(八)激活层实现
ROS2——配置开发环境(五)