Hdu1231 maximum continuous subsequence (divide and conquer or dynamic gauge or double pointer)

Topic link

http://acm.hdu.edu.cn/showproblem.php?pid=1231

Question

Problem Description

Given K A sequence of integers { N1, N2, ..., NK }, Its arbitrary continuous subsequence can be expressed as { Ni, Ni+1, ...,
Nj }, among 1 <= i <= j <= K. The largest continuous subsequence is the largest sum of all the elements in the continuous subsequence ,
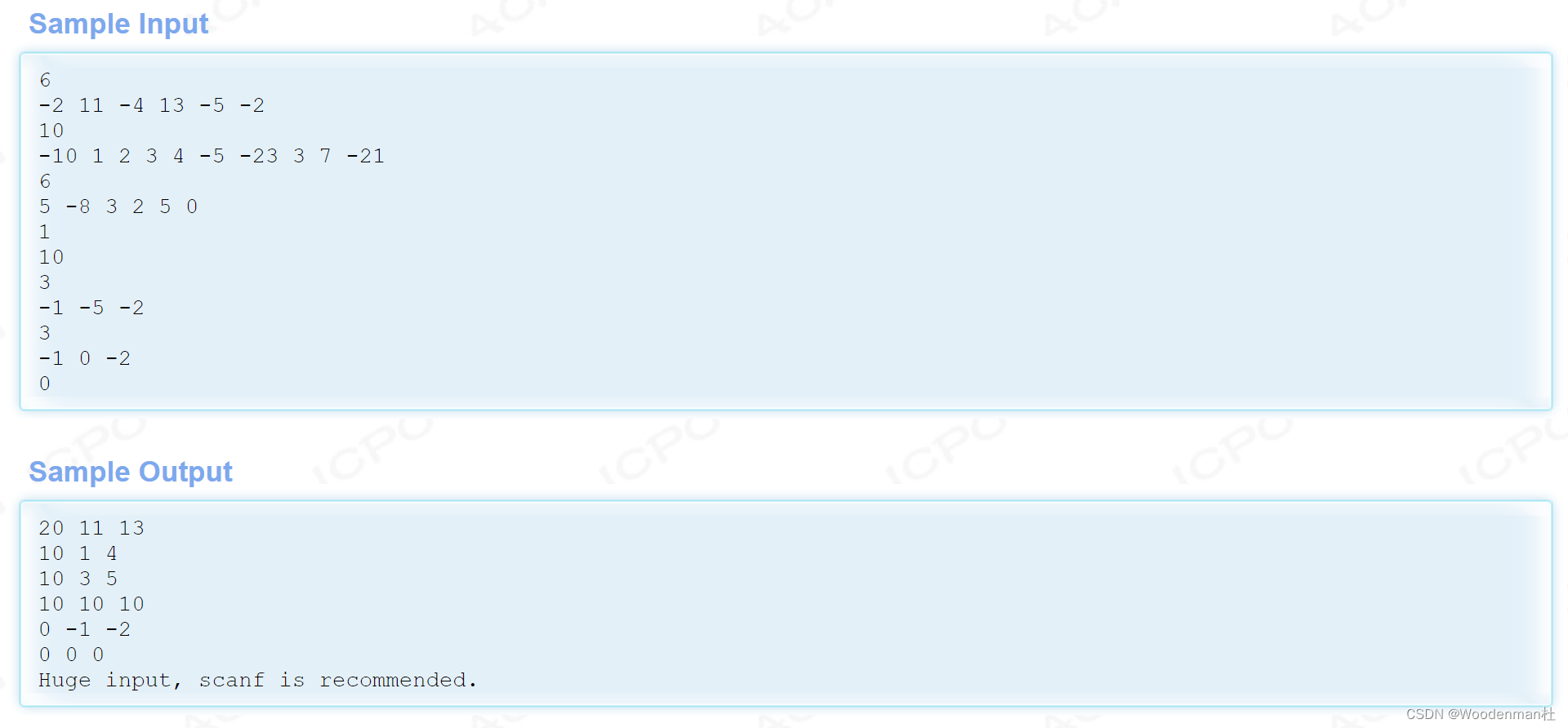
For example, given a sequence { -2, 11, -4, 13, -5, -2 }, The maximum continuous subsequence is { 11, -4, 13 }, Maximum and
by 20.
In this year's data structure examination paper , It is required to write the program to get the maximum and , Now add a request , That is, you also need to output the
The first and last elements of the subsequence .

Input

The test input contains several test cases , Each test case accounts for 2 That's ok , The first 1 Line gives a positive integer K( < 10000 ), The first 2 Line is given K It's an integer , Space between . When K by 0 when , End of input , The use case is not processed .

Output

For each test case , stay 1 Output the maximum sum in the line 、 The first and last elements of the maximal continuous subsequence
plain , Space between . If the largest continuous subsequence is not unique , Then the serial number is output i and j The youngest one （ As shown in the... Of the input sample 2、3 Group ）. If all K Both elements are negative numbers , Then its maximum sum is defined as 0, Output the beginning and end elements of the whole sequence .

Solve

This question can be said to be very classic

Let's not talk about the practice of enumerating left and right by violence ,n^3 I can't get anywhere , Prefix and optimization is not a good practice .

Dynamic gauge

It is recommended to use Dynamic gauge 、 Or double pointer small simulation . But in fact, the idea is very simple

Describe the ：

At first l and r All point to the starting point , then r turn right , At the same time, we calculate l To r And , If the sum is positive , that r Just go straight to the right , If less than or equal to 0, It shows that this addition is not the desired result ( And it's meaningless ), let l = r, Start adding again , Until the last number is added , During this period, the results of the maximum sum are constantly updated res 

See the code later , I really can't explain this nonsense

Divide and conquer

I used to listen to data structures Divide and conquer It's the same question , Let me just talk about the train of thought , The code is gone ：

The so-called divide and conquer is to constantly split a problem into multiple sub problems to deal with

For this question , Let's discuss first A state ：

from l To r The maximum continuous sequence sum of , Nothing but exists in  l To mid(mid = （l+r）/ 2) perhaps mid+1 To r In , Or include mid , There are... On the left and right , Then we need to take out the maximum continuous sequence sum of the three cases to take the maximum value

First look at There are... On the left and right The situation of , How can I ask , Directly from mid Spread to both sides separately to add , When will it stop , Can only be added to the boundary to stop .

Because adding a number and getting smaller does not mean that it will not become larger than before , So it can only be added continuously , Keep the maximum value

Look at the maximum continuous sequence and On both sides What about the situation ？

Divide and rule , Divide and rule , Then just split the sequence into two parts and continue the above process , When there is only one element left, it is the boundary , Less than 0 The number of has no additive meaning , Positive numbers can be added directly

Pseudo code Write about the , Because I never believe in my ability to describe ：

int solve(int l, int r)
{
	// When there is only one element  
	if(l == r){
		if( This element  < 0) return 0;
		else return  This element ; 
	}
	
	int mid = (l + r) / 2;
	// Left bound maximum 
	int left = solve(l, mid);
	// The right bound is the largest 
	int right = solve(mid + 1, r);
	
	// Including the middle bound 
	int l_num, r_num; 
	for mid to l
		l_num = max(l_num, mid To l Elements and )
	for mid to r
		r_num = max(r_num, mid To r Elements and )
	// Take the maximum value to return  
	return max(l_num + r_num, left, right);
} 

AC Code

#include <iostream>
#include <cstring>
#include <cstdio>
#define N 10000
using namespace std;
int n, a[N+1];
int main(void)
{
	while(~scanf("%d", &n))
	{
		if(n == 0) break;	// Run end judgment  
		bool ans = false;	// Total negative number discrimination  
		for(int i = 1; i <= n; i++){
			scanf("%d", &a[i]); 
			if(a[i] >= 0) ans = true;
		}
		if(!ans){	// All negative numbers  
			cout <<0 <<" " <<a[1] <<" " <<a[n] <<endl;
			continue;
		}
		// It turns out that  
		int l, r, resl, resr, res = -1e9, dp = 0;
		l = r = resl = resr = 1; 
		for(int i = 1; i <= n; i++){
			if(dp > 0){               // The sum of elements is greater than 0, Add elements directly 
				dp += a[i];
				r++;
			}else{                    // The sum of elements is less than or equal to 0, Press 0 Additive elements 
				dp = a[i];
				l = r = i;            // Update the left and right boundaries 
			}
			if(dp > res){
				res = dp;              // Update Max 
				resl = l; resr = r;    // Update the left and right boundaries 
			}
		}
		cout <<res <<" " <<a[resl] <<" " <<a[resr] <<endl;
	}
	return 0;
}