The number of occurrences of numbers in the offer 56 array (XOR)

The number of occurrences of numbers in an array I

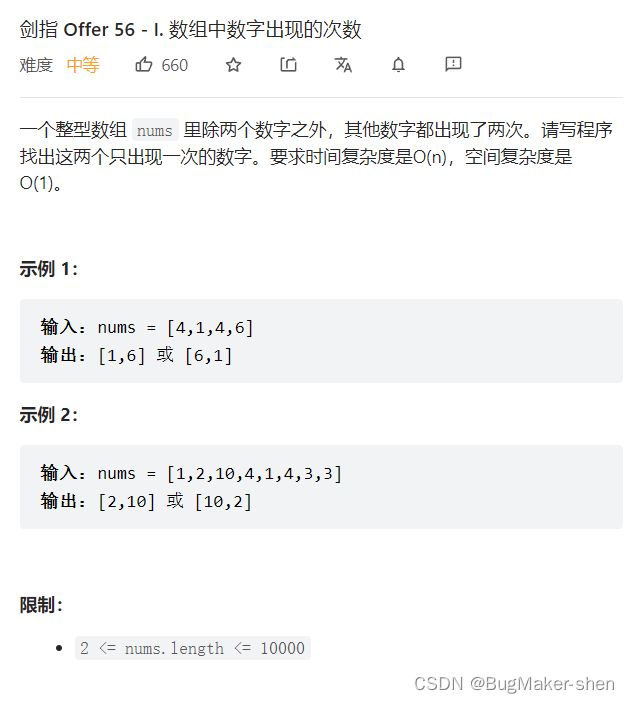
The finger of the sword Offer 56 - I. The number of occurrences of numbers in an array

The same number is XOR 0, Different XORs are 1,0 And any number is XOR equal to the number itself

therefore , All numbers in the array are XOR = Target two numbers XOR . Because these two numbers are different , So the XOR result must not be 0

Suppose the binary result of array XOR is 10010, Then it means that these two targets number from right to left 2 position bit Is different

Then you can use the second digit of all the numbers in the array bit by 0 perhaps 1 Divide the array into 2 individual

In this way, the target number must be scattered in different arrays , And the same number must fall in the same array

The numbers in these two arrays are XOR respectively , The result is the answer

class Solution {
    
public:
    vector<int> singleNumbers(vector<int>& nums) {
    
        int res = 0;
        for(int val : nums){
    
            res ^= val;
        }
        int index = 0;
        while((res & 1) == 0){
    
            //  This loop is used to find which of the two target numbers bit Different , Use this bit Separate the two target numbers 
            //  One of the XOR results bit by 1, Then it means that the two target numbers should bit Different 
            res >>= 1;
            index++;
        }

        int num1 = 0;
        int num2 = 0;
        for(int val : nums){
    
            //  According to one bit Whether to group the same 
            if(((val >> index)  & 1) == 1){
    
                num1 ^= val;
            }else{
    
                num2 ^= val;
            }
        }
        return {
    num1, num2};
    }
};

The number of occurrences of numbers in an array II

The number of occurrences of numbers in an array II

1. Method 1 ： An operation

0 ^ x  = x
x ^ x  = 0
x & ~x = 0
x & ~0 = x

In limine a = 0,b = 0

x First appearance ：a = (a ^ x) & ~b As the result of the a = x, At this time because a = x 了 ,b = (b ^ x) & ~a As the result of the b = 0;

x The second time ：a = (a ^ x) & ~b, a = (x ^ x) & ~0,a = 0; b = (b ^ x) & ~a Simplification , b = (0 ^ x) & ~0 ,b = x;

x A third time ：a = (a ^ x) & ~b, a = (0 ^ x) & ~x ,a = 0; b = (b ^ x) & ~a Simplification , b = (x ^ x) & ~0, b = 0

So three times the same number ,a and b It's all back to 0; Only once , According to the above x The law of the first time is known a = x,b = 0; So finally return to a

class Solution {
    
public:
    int singleNumber(vector<int>& nums) {
    
        int a = 0;
        int b = 0;
        for(int num : nums){
    
            a = (a ^ num) & ~b;
            b = (b ^ num) & ~a;
        }
        return a;
    }
};

2. Method 2 ： Count the bits in all binary representations

Create a length of 32 Array of countscounts , Through the above method, the of each binary bit of all numbers can be recorded 11 Number of occurrences of

int count[32] = {
    0};
    for(int num : nums){
    
        for(int i = 31; i >= 0; i--){
    
        	//  Index small subscript , Store in high position ; Index large subscript , Store in low position 
            count[i] += (num & 1);
            num >>= 1;                
        }
    }

take countscounts Each element pair 33 Seeking remainder , The result is “ A number that appears only once ” Each binary bit of
utilize Move left operation and Or operations , Can be counts The value of each binary in the array is restored to the number res On

	for(int i = 0; i < 32; i++){
    
    	//  When you recover , To recover from the high position , That is, start with a small subscript 
        ans <<= 1;
        ans |= (count[i] % mod);
    }

Use an array to count the bits in all binary representations , How many times 1 Write it all down , Finally, use the statistical data of this array to recover

for example ：3,4,3,3

3 ：   11
4 ：  100
3 ：   11
3 ：   11

Array count Element is ：[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,3,3]

On final recovery , Recover from high to low , Yes count Elements of array mod 3, Then restore

class Solution {
    
public:
    int singleNumber(vector<int>& nums) {
    
        int count[32] = {
    0};
        for(int num : nums){
    
            for(int i = 31; i >= 0; i--){
    
            	//  Index small subscript , Store in high position ; Index large subscript , Store in low position 
                count[i] += (num & 1);
                num >>= 1;                
            }
        }

        int ans = 0;
        int mod = 3;
        for(int i = 0; i < 32; i++){
    
        	//  When you recover , To recover from the high position , That is, start with a small subscript 
            ans <<= 1;
            ans |= (count[i] % mod);
        }
        return ans;
    }
};

actually , Just modify the remainder value m , It can be solved except for one number , The rest of the numbers appear m Time The general problem of