当前位置:网站首页>Application of MATLAB in Linear Algebra (4): similar matrix and quadratic form
Application of MATLAB in Linear Algebra (4): similar matrix and quadratic form
2022-07-05 07:03:00 【Wen Yu is solemn】
Sometimes we need exact eigenvalues and eigenvectors , You have to use Matlab Symbol operation function of .
stay Matlab The form of creating a symbolic matrix in is very similar to that of creating a numerical matrix , Just use symbols to define functions sym.
The following describes several forms of using this function to create a symbol matrix .
1、 Use sym Function directly creates the symbol matrix
This method is almost the same as the method of directly creating numerical matrix .
Matrix elements can be symbolic expressions , various The length of the symbolic expression can be different , Matrix elements can be separated by spaces or commas .
for example :
x=sym('[a+sin(d),b;1/c,d]'); y=det(x)
Get y=(d*c*a+d*c*sin(d)-b)/c
2、 Convert numerical matrix into symbolic matrix
stay Matlab in , Numerical matrices cannot be directly involved in symbolic operations , Must first be converted into a symbolic matrix .
for example :
a=[2/3,sqrt(2);3,1]
a=
0.66671.4142
3.00001.0000
b=sym(a)
b=
[ 2/3, sqrt(2)]
[3,1]
3、 Indexing and modification of symbol matrix
Matlab The index and modification of the symbol matrix of is exactly the same as that of the numerical matrix .
for example :
For the matrix in the above example b Make changes
b(2,2)='log(9)'
01
—
Find an orthogonal transformation x = Py ÿ
边栏推荐
- Use ffmpeg to rotate, flip up and down, and flip horizontally
- Ros2 - Service Service (IX)
- Marvell 88E1515 PHY loopback模式测试
- Special training of C language array
- Preemption of CFS scheduling
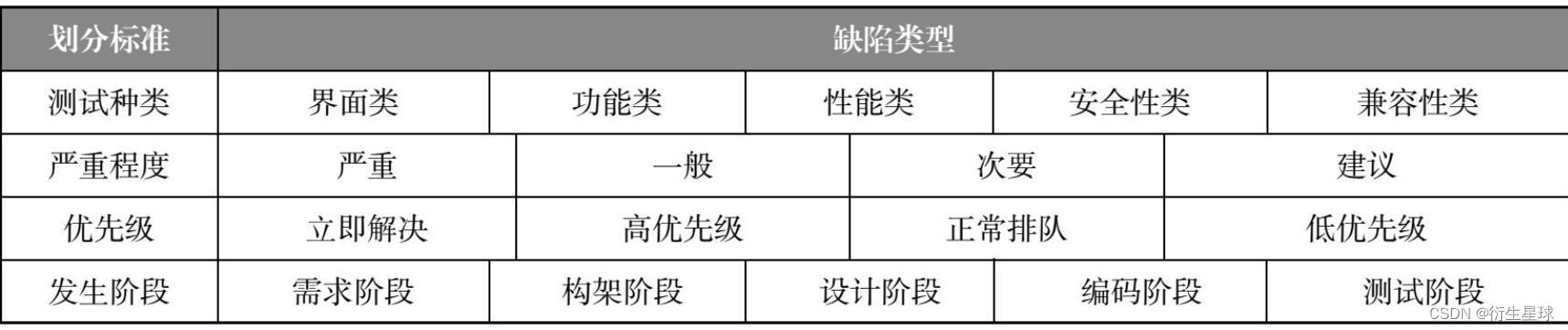
- 【软件测试】02 -- 软件缺陷管理
- 现在有html文件,和用vs制作的mvc(连接了数据库),怎么两个相连?
- Interpretation of the earliest sketches - image translation work sketchygan
- 摄像头的MIPI接口、DVP接口和CSI接口
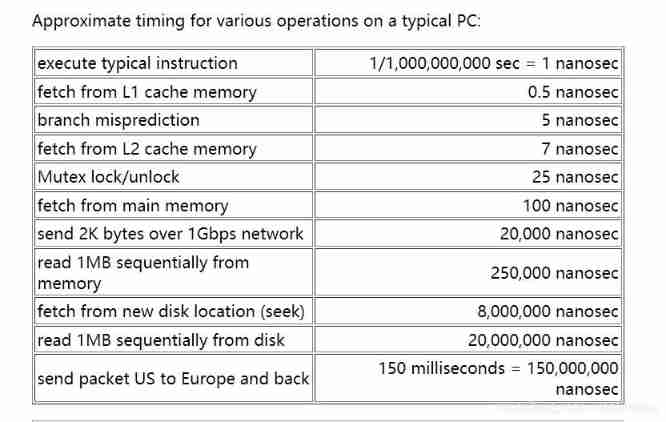
- Instruction execution time
猜你喜欢
随机推荐
Cookie、Session、JWT、token四者间的区别与联系
Vscode editor
Instruction execution time
The problem of Chinese garbled code in the vscode output box can be solved once for life
iNFTnews | 喝茶送虚拟股票?浅析奈雪的茶“发币”
mingling
三体目标管理笔记
【无标题】
基于FPGA的一维卷积神经网络CNN的实现(八)激活层实现
Huawei bracelet, how to add medicine reminder?
程序中的负数存储及类型转换
你心目中的数据分析 Top 1 选 Pandas 还是选 SQL?
ROS2——配置开发环境(五)
【软件测试】04 -- 软件测试与软件开发
6-2 sequence table operation set
[nvidia] CUDA_ VISIBLE_ DEVICES
Xiaomi written test real question 1
Get class files and attributes by reflection
Speedtree01 generator properties
PHY drive commissioning --- mdio/mdc interface Clause 22 and 45 (I)