当前位置:网站首页>[mathematical basis of machine learning] (I) linear algebra (Part 1 +)
[mathematical basis of machine learning] (I) linear algebra (Part 1 +)
2022-07-04 18:56:00 【Binary artificial intelligence】
【 The mathematical basis of machine learning 】( One ) linear algebra (Linear Algebra)( On )
2 linear algebra (Linear Algebra)( On +)
2.3 The solution of linear equations
Earlier, we introduced the general form of equations , namely :
a 11 x 1 + ⋯ + a 1 n x n = b 1 ⋮ a m 1 x 1 + ⋯ + a m n x n = b m \begin{aligned}a_{11} x_{1}+\cdots+a_{1 n} x_{n} &=b_{1} \\& \vdots \\a_{m 1} x_{1}+\cdots+a_{m n} x_{n} &=b_{m}\end{aligned} a11x1+⋯+a1nxnam1x1+⋯+amnxn=b1⋮=bm
among a i j ∈ R a_{i j} \in \mathbb{R} aij∈R, b i ∈ R b_{i} \in \mathbb{R} bi∈R Is a known constant , x j x_j xj Is an unknown quantity , i = 1 , … , m , j = 1 , … , n i=1, \ldots, m, j=1, \ldots, n i=1,…,m,j=1,…,n. up to now , We see that matrix can be used as a concise method to express linear equations , In this way, we can write the linear equations as A x = b \boldsymbol{A}\boldsymbol{x}=\boldsymbol{b} Ax=b. Besides , We also define the basic matrix operations , Such as matrix addition and multiplication . below , We will focus on the solution of linear equations , An algorithm for finding the inverse of matrix is provided .
2.3.1 Special solution and general solution
Before discussing how to solve linear equations , Let's start with an example . Consider the system of equations
[ 1 0 8 − 4 0 1 2 12 ] [ x 1 x 2 x 3 x 4 ] = [ 42 8 ] ( 2.38 ) \left[\begin{array}{cccc}1 & 0 & 8 & -4 \\0 & 1 & 2 & 12\end{array}\right]\left[\begin{array}{l}x_{1} \\x_{2} \\x_{3} \\x_{4}\end{array}\right]=\left[\begin{array}{c}42 \\8\end{array}\right]\qquad (2.38) [100182−412]⎣⎢⎢⎡x1x2x3x4⎦⎥⎥⎤=[428](2.38)
This system of equations has two equations and four unknowns . therefore , Generally speaking , We can get an infinite number of solutions . The form of this system of equations is a minimalist form , The first two columns consist of a 0 And a 1 form .
Our goal is to find scalars x 1 , … , x 4 x_{1}, \ldots, x_{4} x1,…,x4, bring ∑ i = 1 4 x i c i = b \sum_{i=1}^{4} x_{i} \boldsymbol{c}_{i}=\boldsymbol{b} ∑i=14xici=b, among c i \boldsymbol{c}_i ci Is the first... Of the matrix i i i Column , b b b Is the of the system of equations (2.38) The right side of the . For this system of equations , This can be done by taking the... In the first column 42 Times and the second column 8 Times the solution :
b = [ 42 8 ] = 42 [ 1 0 ] + 8 [ 0 1 ] \boldsymbol{b}=\left[\begin{array}{c}42 \\8\end{array}\right]=42\left[\begin{array}{l}1 \\0\end{array}\right]+8\left[\begin{array}{l}0 \\1\end{array}\right] b=[428]=42[10]+8[01]
therefore , One solution of the system of equations is [ 42 , 8 , 0 , 0 ] ⊤ [42,8,0,0]^{\top} [42,8,0,0]⊤, This solution is called Special solution (particular solution or special solution).
However , This is not the only solution to this system of linear equations . To get other solutions , We need to creatively use the columns of the matrix to Extraordinary ( non-trivial) Generate vectors in the same way 0 \mathbf{0} 0: The special solution is multiplied by the matrix of the system of equations , Then add... On both sides of the equation at the same time 0 \mathbf{0} 0 Does not affect the equation .
We use the first two columns ( Their form is very simple ) Represents the third column
[ 8 2 ] = 8 [ 1 0 ] + 2 [ 0 1 ] \left[\begin{array}{l}8 \\2\end{array}\right]=8\left[\begin{array}{l}1 \\0\end{array}\right]+2\left[\begin{array}{l}0 \\1\end{array}\right] [82]=8[10]+2[01]
Then there are 0 = 8 c 1 + 2 c 2 − 1 c 3 + 0 c 4 \mathbf{0}=8 \boldsymbol{c}_{1}+2 \boldsymbol{c}_{2}-1 \boldsymbol{c}_{3}+0 \boldsymbol{c}_{4} 0=8c1+2c2−1c3+0c4, Get the solution : ( x 1 , x 2 , x 3 , x 4 ) = ( 8 , 2 , − 1 , 0 ) \left(x_{1}, x_{2}, x_{3}, x_{4}\right)=(8,2,-1,0) (x1,x2,x3,x4)=(8,2,−1,0). in fact , This solution is arbitrary λ 1 ∈ R \lambda_{1} \in \mathbb{R} λ1∈R Scaling will produce 0 \mathbf{0} 0 vector , namely :
[ 1 0 8 − 4 0 1 2 12 ] ( λ 1 [ 8 2 − 1 0 ] ) = λ 1 ( 8 c 1 + 2 c 2 − c 3 ) = 0 \left[\begin{array}{llll}1 & 0 & 8 & -4 \\0 & 1 & 2 & 12\end{array}\right]\left(\lambda_{1}\left[\begin{array}{c}8 \\2 \\-1 \\0\end{array}\right]\right)=\lambda_{1}\left(8 c_{1}+2 c_{2}-c_{3}\right)=\mathbf{0} [100182−412]⎝⎜⎜⎛λ1⎣⎢⎢⎡82−10⎦⎥⎥⎤⎠⎟⎟⎞=λ1(8c1+2c2−c3)=0
similarly , We use the first two columns to represent the fourth column of the matrix in the system of equations , For any λ 2 ∈ R \lambda_{2} \in \mathbb{R} λ2∈R Generate another set 0 \mathbf{0} 0 An extraordinary version of
[ 1 0 8 − 4 0 1 2 12 ] ( λ 2 [ − 4 12 0 − 1 ] ) = λ 2 ( − 4 c 1 + 12 c 2 − c 4 ) = 0 \left[\begin{array}{llll}1 & 0 & 8 & -4 \\0 & 1 & 2 & 12\end{array}\right]\left(\lambda_{2}\left[\begin{array}{c}-4 \\12 \\0 \\-1\end{array}\right]\right)=\lambda_{2}\left(-4 \boldsymbol{c}_{1}+12 \boldsymbol{c}_{2}-\boldsymbol{c}_{4}\right)=\mathbf{0} [100182−412]⎝⎜⎜⎛λ2⎣⎢⎢⎡−4120−1⎦⎥⎥⎤⎠⎟⎟⎞=λ2(−4c1+12c2−c4)=0
Liberate all together , All solutions of the equations are obtained , be called general solution (general solution), Expressed in the form of a set as :
{ x ∈ R 4 : x = [ 42 8 0 0 ] + λ 1 [ 8 2 − 1 0 ] + λ 2 [ − 4 12 0 − 1 ] , λ 1 , λ 2 ∈ R } \left\{x \in \mathbb{R}^{4}: x=\left[\begin{array}{c}42 \\8 \\0 \\0\end{array}\right]+\lambda_{1}\left[\begin{array}{c}8 \\2 \\-1 \\0\end{array}\right]+\lambda_{2}\left[\begin{array}{c}-4 \\12 \\0 \\-1\end{array}\right], \lambda_{1}, \lambda_{2} \in \mathbb{R}\right\} ⎩⎪⎪⎨⎪⎪⎧x∈R4:x=⎣⎢⎢⎡42800⎦⎥⎥⎤+λ1⎣⎢⎢⎡82−10⎦⎥⎥⎤+λ2⎣⎢⎢⎡−4120−1⎦⎥⎥⎤,λ1,λ2∈R⎭⎪⎪⎬⎪⎪⎫
remarks :
The general solution of linear equations includes the following three steps :
- (1) find A x = b Ax=b Ax=b Special solution of .
- (2) find A x = 0 Ax=0 Ax=0 All the solutions of .
- (3) Combine steps (1) and (2) Get the general solution .
- Note that neither the general solution nor the special solution is unique .
The linear equations in the above example are easy to solve , Because the matrix in the system of equations has a particularly simple form , This enables us to obtain the special solution and general solution through the surrogate test . However , The general equations will not be in this simple form .
Fortunately, , There is a constructive algorithm that can convert any system of linear equations into this particularly simple form : Gauss elimination ( Gaussian elimination). The key of Gauss elimination method is the elementary transformation of linear equations , Convert the equations into a simple form . then , We can use the above three steps to solve the linear equations .
2.3.2 Elementary transformation
The key to solving linear equations is Elementary transformation (elementary transformations), It can keep the solution set unchanged , Transform the equations into simpler forms :
- (1) Two equations ( The row of the matrix representing the system of equations ) In exchange for
- (2) equation ( That's ok ) Multiply by a constant λ ∈ R \ { 0 } \lambda \in \mathbb{R} \backslash\{0\} λ∈R\{ 0}
- (3) Two equations ( That's ok ) The addition of
remarks :(1)、(2)、(3) Can be combined .
example 2.6
about a ∈ R a \in \mathbb{R} a∈R, Find all solutions of the following equations :
− 2 x 1 + 4 x 2 − 2 x 3 − x 4 + 4 x 5 = − 3 4 x 1 − 8 x 2 + 3 x 3 − 3 x 4 + x 5 = 2 x 1 − 2 x 2 + x 3 − x 4 + x 5 = 0 x 1 − 2 x 2 − 3 x 4 + 4 x 5 = a \begin{array}{rrrrrrrr}-2 x_{1} & + & 4 x_{2} & - & 2 x_{3} & - & x_{4}&+ & 4 x_{5} & = & -3 \\4 x_{1} & - & 8 x_{2} & + & 3 x_{3} & - & 3 x_{4}&+ & x_{5} & = & 2 \\x_{1} & - & 2 x_{2} & + & x_{3} & - & x_{4}&+ & x_{5} & = & 0 \\x_{1} & - & 2 x_{2} & & & - &3 x_{4} & + & 4 x_{5} & = & a\end{array} −2x14x1x1x1+−−−4x28x22x22x2−++2x33x3x3−−−−x43x4x43x4++++4x5x5x54x5====−320a
We first convert this system of equations into a compact matrix representation A x = b \boldsymbol{A}\boldsymbol{x}=\boldsymbol{b} Ax=b. We no longer explicitly mention variables x \boldsymbol{x} x, It's about building Augmented matrix (augmented matrix)( In the form of [ A ∣ b ] [\boldsymbol{A} \mid \boldsymbol{b}] [A∣b])
We use vertical lines to separate the left and right sides of the equations .
[ − 2 4 − 2 − 1 4 − 3 4 − 8 3 − 3 1 2 1 − 2 1 − 1 1 0 1 − 2 0 − 3 4 a ] Swap with R 3 Swap with R 1 \left[\begin{array}{rrrrr|r}-2 & 4 & -2 & -1 & 4 & -3 \\4 & -8 & 3 & -3 & 1 & 2 \\1 & -2 & 1 & -1 & 1 & 0 \\1 & -2 & 0 & -3 & 4 & a\end{array}\right]\begin{array}{l}\text{Swap with } R_3\\ \\\text{Swap with }R_1 \\\\\end{array} ⎣⎢⎢⎡−24114−8−2−2−2310−1−3−1−34114−320a⎦⎥⎥⎤Swap with R3Swap with R1
Swap the first line R 1 R_1 R1 And the third line R 3 R_3 R3 obtain :
[ 1 − 2 1 − 1 1 0 4 − 8 3 − 3 1 2 − 2 4 − 2 − 1 4 − 3 1 − 2 0 − 3 4 a ] − 4 R 1 + 2 R 1 − R 1 \left[\begin{array}{rrrrr|r}1 & -2 & 1 & -1 & 1 & 0 \\4 & -8 & 3 & -3 & 1 & 2 \\-2 & 4 & -2 & -1 & 4 & -3 \\1 & -2 & 0 & -3 & 4 & a\end{array}\right] \begin{array}{l} \\ -4 R_{1} \\+2 R_{1} \\-R_{1}\end{array} ⎣⎢⎢⎡14−21−2−84−213−20−1−3−1−3114402−3a⎦⎥⎥⎤−4R1+2R1−R1
We use the transformation specified in the above formula ( for example , The above formula includes 2 Line minus four times 1 That's ok ) after , We get
[ 1 − 2 1 − 1 1 0 0 0 − 1 1 − 3 2 0 0 0 − 3 6 − 3 0 0 − 1 − 2 3 a ] \left[\begin{array}{rrrrr|r}1 & -2 & 1 & -1 & 1 & 0 \\0 & 0 & -1 & 1 & -3 & 2 \\0 & 0 & 0 & -3 & 6 & -3 \\0 & 0 & -1 & -2 & 3 & a\end{array}\right] ⎣⎢⎢⎡1000−20001−10−1−11−3−21−36302−3a⎦⎥⎥⎤
We use it ⇝ \rightsquigarrow ⇝ To represent the elementary transformation of the augmented matrix .
[ 1 − 2 1 − 1 1 0 0 0 − 1 1 − 3 2 0 0 0 − 3 6 − 3 0 0 − 1 − 2 3 a ] − R 2 − R 3 \qquad\left[\begin{array}{rrrrr|r}1 & -2 & 1 & -1 & 1 & 0 \\0 & 0 & -1 & 1 & -3 & 2 \\0 & 0 & 0 & -3 & 6 & -3 \\0 & 0 & -1 & -2 & 3 & a\end{array}\right]\begin{array}{l} \\\\\\-R_{2}-R_{3}\end{array} ⎣⎢⎢⎡1000−20001−10−1−11−3−21−36302−3a⎦⎥⎥⎤−R2−R3
⇝ [ 1 − 2 1 − 1 1 0 0 0 − 1 1 − 3 2 0 0 0 − 3 6 − 3 0 0 0 0 0 a + 1 ] ⋅ ( − 1 ) ⋅ ( − 1 3 ) \rightsquigarrow\left[\begin{array}{rrrrr|r}1 & -2 & 1 & -1 & 1 & 0 \\0 & 0 & -1 & 1 & -3 & 2 \\0 & 0 & 0 & -3 & 6 & -3 \\0 & 0 & 0 & 0 & 0 & a+1\end{array}\right] \begin{array}{l} \cdot (-1)\\\cdot (-\frac{1}{3})\\ \end{array} ⇝⎣⎢⎢⎡1000−20001−100−11−301−36002−3a+1⎦⎥⎥⎤⋅(−1)⋅(−31)
⇝ [ 1 − 2 1 − 1 1 0 0 0 1 − 1 3 − 2 0 0 0 1 − 2 1 0 0 0 0 0 a + 1 ] \rightsquigarrow \quad\left[\begin{array}{rrrrr|r}1 & -2 & 1 & -1 & 1 & 0 \\0 & 0 & 1 & -1 & 3 & -2 \\0 & 0 & 0 & 1 & -2 & 1 \\0 & 0 & 0 & 0 & 0 & a+1\end{array}\right]\qquad\qquad ⇝⎣⎢⎢⎡1000−20001100−1−11013−200−21a+1⎦⎥⎥⎤
This ( Augmentation ) The matrix now becomes a simple form —— Line ladder form (row-echelon form,REF). Reduce this compact representation to an explicit representation , We get
x 1 − 2 x 2 + x 3 − x 4 + x 5 = 0 x 3 − x 4 + 3 x 5 = − 2 x 4 − 2 x 5 = 1 0 = a + 1 \begin{array}{rrrrrr} x_{1} & -&2x_{2}&+&x_{3} & -&x_{4}&+ &x_{5} & = & 0 \\&&&&x_{3}&-& x_{4}&+&3 x_{5} & = & -2 \\&&&&& & x_{4}&-&2 x_{5} & = & 1 \\& &&&&&& & 0 & = & a+1\end{array} x1−2x2+x3x3−−x4x4x4++−x53x52x50====0−21a+1
Only when the a = − 1 a=-1 a=−1 The equations have a solution . A special solution is :
[ x 1 x 2 x 3 x 4 x 5 ] = [ 2 0 − 1 1 0 ] \left[\begin{array}{l}x_{1} \\x_{2} \\x_{3} \\x_{4} \\x_{5}\end{array}\right]=\left[\begin{array}{c}2 \\0 \\-1 \\1 \\0\end{array}\right] ⎣⎢⎢⎢⎢⎡x1x2x3x4x5⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡20−110⎦⎥⎥⎥⎥⎤
general solution :
{ x ∈ R 5 : x = [ 2 0 − 1 1 0 ] + λ 1 [ 2 1 0 0 0 ] + λ 2 [ 2 0 − 1 2 1 ] , λ 1 , λ 2 ∈ R } \left\{x \in \mathbb{R}^{5}: x=\left[\begin{array}{c}2 \\0 \\-1 \\1 \\0\end{array}\right]+\lambda_{1}\left[\begin{array}{l}2 \\1 \\0 \\0 \\0\end{array}\right]+\lambda_{2}\left[\begin{array}{c}2 \\0 \\-1 \\2 \\1\end{array}\right], \quad \lambda_{1}, \lambda_{2} \in \mathbb{R}\right\} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧x∈R5:x=⎣⎢⎢⎢⎢⎡20−110⎦⎥⎥⎥⎥⎤+λ1⎣⎢⎢⎢⎢⎡21000⎦⎥⎥⎥⎥⎤+λ2⎣⎢⎢⎢⎢⎡20−121⎦⎥⎥⎥⎥⎤,λ1,λ2∈R⎭⎪⎪⎪⎪⎬⎪⎪⎪⎪⎫
below , We will introduce in detail a constructive method to obtain the special and general solutions of linear equations .
remarks : Principal element and ladder structure
Yes Leading coefficient (leading coefficient, The first non-zero number from the left ) be called Principal component (Pivots ), And always strictly to the right of the principal element of the upper row . therefore , Any row ladder (row-echelon form) All equations have “ ladder (staircase)” structure .
Definition 2.6( Row ladder )
A matrix is Row ladder (row-echelon form) The matrix needs to meet :
- All rows containing only zeros are at the bottom of the matrix ; Accordingly , All rows containing at least one non-zero element are at the top of rows containing only zero .
- Just look at non-zero lines , The first non-zero number from the left ( Also known as principal element or leading coefficient ) Always strictly to the right of the row principal above it .
remarks : Basic and free variables
The variable corresponding to the principal element of the row ladder type is called Basic variables (basic variables), Other variables are called Free variable (free variables).
for example , about
x 1 − 2 x 2 + x 3 − x 4 + x 5 = 0 x 3 − x 4 + 3 x 5 = − 2 x 4 − 2 x 5 = 1 0 = a + 1 \begin{array}{rrrrrr} x_{1} & -&2x_{2}&+&x_{3} & -&x_{4}&+ &x_{5} & = & 0 \\&&&&x_{3}&-& x_{4}&+&3 x_{5} & = & -2 \\&&&&& & x_{4}&-&2 x_{5} & = & 1 \\& &&&&&& & 0 & = & a+1\end{array} x1−2x2+x3x3−−x4x4x4++−x53x52x50====0−21a+1
x 1 , x 3 , x 4 x_1,x_3,x_4 x1,x3,x4 Is the basic variable , x 2 , x 5 x_2,x_5 x2,x5 It's a free variable .
remarks :( Seeking special solution )
When we need to determine a particular solution , The row ladder is convenient for us to solve . To do this , We use the principal component column to represent the right side of the system of equations , namely b = ∑ i = 1 P λ i p i \boldsymbol{b}=\sum_{i=1}^{P} \lambda_{i} \boldsymbol{p}_{i} b=∑i=1Pλipi, among p i , i = 1 , … , P \boldsymbol{p}_{i}, i=1, \ldots, P pi,i=1,…,P The column of the primary element , That is, the main element column .
λ i λ_i λi It's easy to be sure , We can Start with the rightmost primary column , One to the left Once certain .
In the previous example , We're trying to find λ 1 , λ 2 , λ 3 λ_1,λ_2,λ_3 λ1,λ2,λ3, bring :
λ 1 [ 1 0 0 0 ] + λ 2 [ 1 1 0 0 ] + λ 3 [ − 1 − 1 1 0 ] = [ 0 − 2 1 0 ] \lambda_{1}\left[\begin{array}{l}1 \\0 \\0 \\0\end{array}\right]+\lambda_{2}\left[\begin{array}{l}1 \\1 \\0 \\0\end{array}\right]+\lambda_{3}\left[\begin{array}{c}-1 \\-1 \\1 \\0\end{array}\right]=\left[\begin{array}{c}0 \\-2 \\1 \\0\end{array}\right] λ1⎣⎢⎢⎡1000⎦⎥⎥⎤+λ2⎣⎢⎢⎡1100⎦⎥⎥⎤+λ3⎣⎢⎢⎡−1−110⎦⎥⎥⎤=⎣⎢⎢⎡0−210⎦⎥⎥⎤
From here , We find relatively intuitively λ 3 = 1 , λ 2 = − 1 , λ 1 = 2 \lambda_{3}=1, \lambda_{2}=-1, \lambda_{1}=2 λ3=1,λ2=−1,λ1=2. For non principal Columns , We implicitly set its coefficient to 0. therefore , We get the special solution as : [ 2 , 0 , − 1 , 1 , 0 ] ⊤ [2,0,-1,1,0]^{\top} [2,0,−1,1,0]⊤
remarks : The simplest step
A system of equations is The simplest step (Reduced Row Echelon Form, Also known as row-reduced echelon form or row canonical form) Need to meet :
- It's a row ladder
- Each principal element is 1
- The principal element is the only non-zero item in its column .
The simplest step of the line will be in the next 2.3.3 Section plays an important role , Because it allows us to directly determine the general solution of linear equations
remarks : Gauss elimination
Gauss elimination (Gaussian elimination) It is an algorithm that transforms a system of linear equations into a row simplest ladder type through elementary transformation .
example 2.7 The simplest step
There are the following lines of the simplest ladder matrix ( bold 1 The main element ):
A = [ 1 3 0 0 3 0 0 1 0 9 0 0 0 1 − 4 ] ( 2.49 ) \boldsymbol{A}=\left[\begin{array}{ccccc}\mathbf{1} & 3 & 0 & 0 & 3 \\0 & 0 & \mathbf{1} & 0 & 9 \\0 & 0 & 0 & \mathbf{1} & -4\end{array}\right]\qquad (2.49) A=⎣⎡10030001000139−4⎦⎤(2.49)
seek A x = 0 \boldsymbol{A}\boldsymbol{x}=\boldsymbol{0} Ax=0 The key to the solution of is the non principal element column , We need to express it as the of the primary column ( linear ) Combine ; The simplest ladder makes this relatively simple . We use the sum of multiples of the principal column on the left to represent the non principal column :
The second column is the... Of the first column 3 times ( We can ignore the primary column to the right of the second column ). therefore , In order to get 0 \mathbf{0} 0, We need to subtract the second column from three times the first column .
Now? , Let's look at the second non principal column —— The fifth column .
The fifth column can be composed of... Of the first principal column 3 times 、 Of the second principal column 9 times And the third principal column −4 times Express . We need to use the index of the primary column , And convert the fifth column to the... Of the first column 3 times 、 Second column ( Non principal column ) Of 0 times 、 The third column ( The second non principal column ) Of 9 Times and the fourth column -4 times ( That is, the third principal element column ) The sum of the , Then subtract the fifth column to get 0 \mathbf{0} 0. Last , You can solve this homogeneous system of equations .
All in all , A x = 0 , x ∈ R 5 \boldsymbol{A} \boldsymbol{x}=0, \boldsymbol{x} \in \mathbb{R}^{5} Ax=0,x∈R5 All solutions of are given by
{ x ∈ R 5 : x = λ 1 [ 3 − 1 0 0 0 ] + λ 2 [ 3 0 9 − 4 − 1 ] , λ 1 , λ 2 ∈ R } ( 2.50 ) \left\{\boldsymbol{x} \in \mathbb{R}^{5}: \boldsymbol{x}=\lambda_{1}\left[\begin{array}{c}3 \\-1 \\0 \\0 \\0\end{array}\right]+\lambda_{2}\left[\begin{array}{c}3 \\0 \\9 \\-4 \\-1\end{array}\right], \quad \lambda_{1}, \lambda_{2} \in \mathbb{R}\right\}\qquad(2.50) ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧x∈R5:x=λ1⎣⎢⎢⎢⎢⎡3−1000⎦⎥⎥⎥⎥⎤+λ2⎣⎢⎢⎢⎢⎡309−4−1⎦⎥⎥⎥⎥⎤,λ1,λ2∈R⎭⎪⎪⎪⎪⎬⎪⎪⎪⎪⎫(2.50)
2.3.3 Minus-1 skill
below , We will introduce a practical technique to solve homogeneous linear equations A x = 0 \boldsymbol{A}\boldsymbol{x}=\boldsymbol{0} Ax=0 Solution x \boldsymbol{x} x, among A ∈ R k × n , x ∈ R n \boldsymbol{A} \in \mathbb{R}^{k \times n}, \boldsymbol{x} \in \mathbb{R}^{n} A∈Rk×n,x∈Rn
First , We assume that A \boldsymbol{A} A yes The simplest step , And there are no rows that contain only zeros , namely :
A = [ 0 ⋯ 0 1 ∗ ⋯ ∗ 0 ∗ ⋯ ∗ 0 ∗ ⋯ ∗ ⋮ ⋮ 0 0 ⋯ 0 1 ∗ ⋯ ∗ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 ⋮ ⋮ 0 ⋯ 0 0 0 ⋯ 0 0 0 ⋯ 0 1 ∗ ⋯ ∗ ] \boldsymbol{A}=\left[\begin{array}{ccccccccccccccc}0 & \cdots & 0 & \mathbf{1} & * & \cdots & * & 0 & * & \cdots & * & 0 & * & \cdots & * \\\vdots & & \vdots & 0 & 0 & \cdots & 0 & \mathbf{1} & * & \cdots & * & \vdots & \vdots & & \vdots \\\vdots & & \vdots & \vdots & \vdots & & \vdots & 0 & \vdots & & \vdots & \vdots & \vdots & & \vdots \\\vdots & & \vdots & \vdots & \vdots & & \vdots & \vdots & \vdots & & \vdots & 0 & \vdots & & \vdots \\0 & \cdots & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & \cdots & 0 & 1 & * & \cdots & *\end{array}\right] A=⎣⎢⎢⎢⎢⎢⎢⎢⎡0⋮⋮⋮0⋯⋯0⋮⋮⋮010⋮⋮0∗0⋮⋮0⋯⋯⋯∗0⋮⋮0010⋮0∗∗⋮⋮0⋯⋯⋯∗∗⋮⋮00⋮⋮01∗⋮⋮⋮∗⋯⋯∗⋮⋮⋮∗⎦⎥⎥⎥⎥⎥⎥⎥⎤
among ∗ * ∗ Is a random real number , A \boldsymbol{A} A The first non-zero item of each line must be 1, All other items in the corresponding column must be 0.
Columns with principal elements j 1 , … , j k j_{1}, \ldots, j_{k} j1,…,jk( Mark it in bold ) Is the standard unit vector e 1 , … , e k ∈ R k e_{1}, \ldots, e_{k} \in \mathbb{R}^{k} e1,…,ek∈Rk. We add n − k n−k n−k Expand the matrix to n × n n×n n×n- matrix A ~ \tilde{\boldsymbol{A}} A~, The form of the line added by the extension is :
[ 0 ⋯ 0 − 1 0 ⋯ 0 ] ( 2.52 ) \left[\begin{array}{lllllll}0 & \cdots & 0 & -1 & 0 & \cdots & 0\end{array}\right]\qquad (2.52) [0⋯0−10⋯0](2.52)
So the augmented matrix A ~ \tilde{\boldsymbol{A}} A~ The diagonal of contains 1 or -1. then , contain −1 The column as the principal element is a system of homogeneous equations A x = 0 \boldsymbol{A}\boldsymbol{x}=\boldsymbol{0} Ax=0 Solution . More precisely , These columns make up A x = 0 \boldsymbol{A}\boldsymbol{x}=\boldsymbol{0} Ax=0 Basis of solution space , We also call it kernel or zero space ( see 2.7.3 section ).
example 8 (Minus-1 Trick)
about (2.49) This simplest step (REF) matrix :
A = [ 1 3 0 0 3 0 0 1 0 9 0 0 0 1 − 4 ] \boldsymbol{A}=\left[\begin{array}{ccccc}1 & 3 & 0 & 0 & 3 \\0 & 0 & 1 & 0 & 9 \\0 & 0 & 0 & 1 & -4\end{array}\right] A=⎣⎡10030001000139−4⎦⎤
Now let's add... Where the principal element is missing on the diagonal (2.52) Lines of form , Expand this matrix into a 5 × 5 Matrix
A ~ = [ 1 3 0 0 3 0 − 1 0 0 0 0 0 1 0 9 0 0 0 1 − 4 0 0 0 0 − 1 ] \tilde{\boldsymbol{A}}=\left[\begin{array}{ccccc}1 & 3 & 0 & 0 & 3 \\\textcolor{blue}{0} & \textcolor{blue}{-1} & \textcolor{blue}{0} & \textcolor{blue}{0} & \textcolor{blue}{0} \\0 & 0 & 1 & 0 & 9 \\0 & 0 & 0 & 1 & -4 \\\textcolor{blue}{0} & \textcolor{blue}{0} & \textcolor{blue}{0} & \textcolor{blue}{0} & \textcolor{blue}{-1}\end{array}\right] A~=⎣⎢⎢⎢⎢⎡100003−10000010000010309−4−1⎦⎥⎥⎥⎥⎤
We can take A ~ \tilde{\boldsymbol{A}} A~ It contains... On the diagonal -1 Columns of , Get... Immediately A x = 0 \boldsymbol{A}\boldsymbol{x}=\boldsymbol{0} Ax=0 Solution :
{ x ∈ R 5 : x = λ 1 [ 3 − 1 0 0 0 ] + λ 2 [ 3 0 9 − 4 − 1 ] , λ 1 , λ 2 ∈ R } } \left\{\begin{array}{l}\left.x \in \mathbb{R}^{5}: \boldsymbol{x}=\lambda_{1}\left[\begin{array}{c}3 \\-1 \\0 \\0 \\0\end{array}\right]+\lambda_{2}\left[\begin{array}{c}3 \\0 \\9 \\-4 \\-1\end{array}\right], \quad \lambda_{1}, \lambda_{2} \in \mathbb{R}\right\}\end{array}\right\} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧x∈R5:x=λ1⎣⎢⎢⎢⎢⎡3−1000⎦⎥⎥⎥⎥⎤+λ2⎣⎢⎢⎢⎢⎡309−4−1⎦⎥⎥⎥⎥⎤,λ1,λ2∈R⎭⎪⎪⎪⎪⎬⎪⎪⎪⎪⎫⎭⎪⎪⎪⎪⎬⎪⎪⎪⎪⎫
And example 2.7 Same result for .
Seeking inverse
For calculation A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n The inverse of A − 1 \boldsymbol{A}^{-1} A−1, We need to find satisfaction A X = I n \boldsymbol{A X}=\boldsymbol{I}_{n} AX=In Matrix X \boldsymbol{X} X. X = A − 1 \boldsymbol{X}=\boldsymbol{A}^{-1} X=A−1. We can write it as a set of linear equations A X = I n \boldsymbol{A X}=\boldsymbol{I}_{n} AX=In And solve X = [ x 1 ∣ ⋯ ∣ x n ] \boldsymbol{X}=\left[\boldsymbol{x}_{1}|\cdots| \boldsymbol{x}_{n}\right] X=[x1∣⋯∣xn]. We use augmented matrix representation to represent this set of linear equations , And make the following transformation :
[ A ∣ I n ] ⇝ ⋯ ⇝ [ I n ∣ A − 1 ] \left[\boldsymbol{A} \mid \boldsymbol{I}_{n}\right] \quad \rightsquigarrow \cdots \rightsquigarrow \quad\left[\boldsymbol{I}_{n} \mid \boldsymbol{A}^{-1}\right] [A∣In]⇝⋯⇝[In∣A−1]
It means , If we simplify the augmented system of equations into a row simplest ladder , We can read the inverse of the matrix on the right-hand side of the equations . therefore , Determining the inverse matrix of a matrix is equivalent to solving a system of linear equations .
example 2.9 Use Gauss elimination method to find the inverse matrix
seek
A = [ 1 0 2 0 1 1 0 0 1 2 0 1 1 1 1 1 ] \boldsymbol{A}=\left[\begin{array}{llll}1 & 0 & 2 & 0 \\1 & 1 & 0 & 0 \\1 & 2 & 0 & 1 \\1 & 1 & 1 & 1\end{array}\right] A=⎣⎢⎢⎡1111012120010011⎦⎥⎥⎤
The inverse of .
Let's write the augmented matrix
[ 1 0 2 0 1 0 0 0 1 1 0 0 0 1 0 0 1 2 0 1 0 0 1 0 1 1 1 1 0 0 0 1 ] \left[\begin{array}{cccc|cccc}1 & 0 & 2 & 0 & 1 & 0 & 0 & 0 \\1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 \\1 & 2 & 0 & 1 & 0 & 0 & 1 & 0 \\1 & 1 & 1 & 1 & 0 & 0 & 0 & 1\end{array}\right] ⎣⎢⎢⎡11110121200100111000010000100001⎦⎥⎥⎤
The Gauss elimination method is used to transform it into the simplest step :
[ 1 0 0 0 − 1 2 − 2 2 0 1 0 0 1 − 1 2 − 2 0 0 1 0 1 − 1 1 − 1 0 0 0 1 − 1 0 − 1 2 ] \left[\begin{array}{cccc|cccc}1 & 0 & 0 & 0 & -1 & 2 & -2 & 2 \\0 & 1 & 0 & 0 & 1 & -1 & 2 & -2 \\0 & 0 & 1 & 0 & 1 & -1 & 1 & -1 \\0 & 0 & 0 & 1 & -1 & 0 & -1 & 2\end{array}\right] ⎣⎢⎢⎡1000010000100001−111−12−1−10−221−12−2−12⎦⎥⎥⎤
such , The required inverse matrix is given on the right :
A − 1 = [ − 1 2 − 2 2 1 − 1 2 − 2 1 − 1 1 − 1 − 1 0 − 1 2 ] \boldsymbol{A}^{-1}=\left[\begin{array}{cccc}-1 & 2 & -2 & 2 \\1 & -1 & 2 & -2 \\1 & -1 & 1 & -1 \\-1 & 0 & -1 & 2\end{array}\right] A−1=⎣⎢⎢⎡−111−12−1−10−221−12−2−12⎦⎥⎥⎤
We can perform multiplication A A − 1 \boldsymbol{A} \boldsymbol{A}^{-1} AA−1 Is it equal to I 4 \boldsymbol{I}_4 I4 To test .
2.3.4 Algorithm for solving linear equations
In the following , We will briefly discuss A x = b \boldsymbol{A}\boldsymbol{x}=\boldsymbol{b} Ax=b The solution method of linear equations in form . Here we assume that there is a solution . If there is no solution , We need to resort to approximate solutions , Such as linear regression in Chapter 9 , There is no introduction here .
If we can determine the inverse A − 1 \boldsymbol{A}^{−1} A−1, that A x = b \boldsymbol{A}\boldsymbol{x}=\boldsymbol{b} Ax=b The solution of is expressed as x = A − 1 b \boldsymbol{x}=\boldsymbol{A}^{-1} \boldsymbol{b} x=A−1b. However , Only when A \boldsymbol{A} A When it is a square matrix and reversible , That's how it works , But it's not usually the case . however , Under appropriate assumptions ( namely A \boldsymbol{A} A Need to have linearly independent columns ), We can use the following transformations :
A x = b * A ⊤ A x = A ⊤ b * x = ( A ⊤ A ) − 1 A ⊤ b \boldsymbol{A} \boldsymbol{x}=\boldsymbol{b} \Longleftrightarrow \boldsymbol{A}^{\top} \boldsymbol{A} \boldsymbol{x}=\boldsymbol{A}^{\top} \boldsymbol{b} \Longleftrightarrow \boldsymbol{x}=\left(\boldsymbol{A}^{\top} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\top} \boldsymbol{b} Ax=b*A⊤Ax=A⊤b*x=(A⊤A)−1A⊤b
That is to use Moore-Penrose Pseudo inverse (Moore-Penrose pseudo-inverse) ( A ⊤ A ) − 1 A ⊤ \left(\boldsymbol{A}^{\top} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\top} (A⊤A)−1A⊤ To make sure A x = b \boldsymbol{A}\boldsymbol{x}=\boldsymbol{b} Ax=b Of Moore-Penrose Pseudo inverse solution ( A ⊤ A ) − 1 A ⊤ b \left(\boldsymbol{A}^{\top} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\top}\boldsymbol{b} (A⊤A)−1A⊤b, This also corresponds to the solution of the minimum norm least squares method .
The disadvantage of this method is that it needs to sum the product of the matrix A ⊤ A \boldsymbol{A}^{\top} \boldsymbol{A} A⊤A Do a lot of calculations . Besides , For reasons of numerical accuracy , It is generally not recommended to calculate inverse or pseudo inverse . therefore , In the following , We will briefly discuss other methods for solving linear equations .
Gauss elimination method is used to calculate determinant 、 Check whether the vector set is linearly independent 、 Calculate the inverse of the matrix , Calculate the rank of the matrix , And determining the basis of vector space . Gauss elimination method is an intuitive and constructive method to solve a system of linear equations with thousands of variables . However , For a system of equations with millions of variables , This is impractical , Because the amount of computation required increases according to the cubic of the number of simultaneous equations .
In practice , Many linear equations are solved by Steady iterative method (stationary iterative methods) Indirectly solved , Such as Richardson Method 、Jacobi Method 、Gauß-Seidel Method and successive over relaxation method , or Krylov Subspace method , Such as conjugate gradient 、 Generalized minimum residual or biconjugate gradient .
set up x ∗ \boldsymbol{x}_{*} x∗ yes A x = b \boldsymbol{A}\boldsymbol{x}=\boldsymbol{b} Ax=b Solution . The key idea of these iterative methods is to establish the following forms of iteration
x ( k + 1 ) = C x ( k ) + d \boldsymbol{x}^{(k+1)}=\boldsymbol{C} \boldsymbol{x}^{(k)}+\boldsymbol{d} x(k+1)=Cx(k)+d
By looking for the right C \boldsymbol{C} C and d \boldsymbol{d} d, Reduce the residual in each iteration ∥ x ( k + 1 ) − x ∗ ∥ \left\|\boldsymbol{x}^{(k+1)}-\boldsymbol{x}_{*}\right\| ∥∥x(k+1)−x∗∥∥ Until it converges to x ∗ \boldsymbol{x}_{*} x∗. We will be in 3.1 Section introduces norm ∥ ⋅ ∥ \|\cdot\| ∥⋅∥, It allows us to calculate the similarity between vectors .
边栏推荐
- Interpretation of SIGMOD '22 hiengine paper
- ByteDance dev better technology salon was successfully held, and we joined hands with Huatai to share our experience in improving the efficiency of web research and development
- 中国农科院基因组所汪鸿儒课题组诚邀加入
- The block:usdd has strong growth momentum
- 其他InterSystems %Net工具
- Scala基础教程--17--集合
- Halcon template matching
- ThreadLocal原理与使用
- Halcon模板匹配
- 资料下载 丨首届腾讯技术开放日课程精华!
猜你喜欢

How to improve development quality
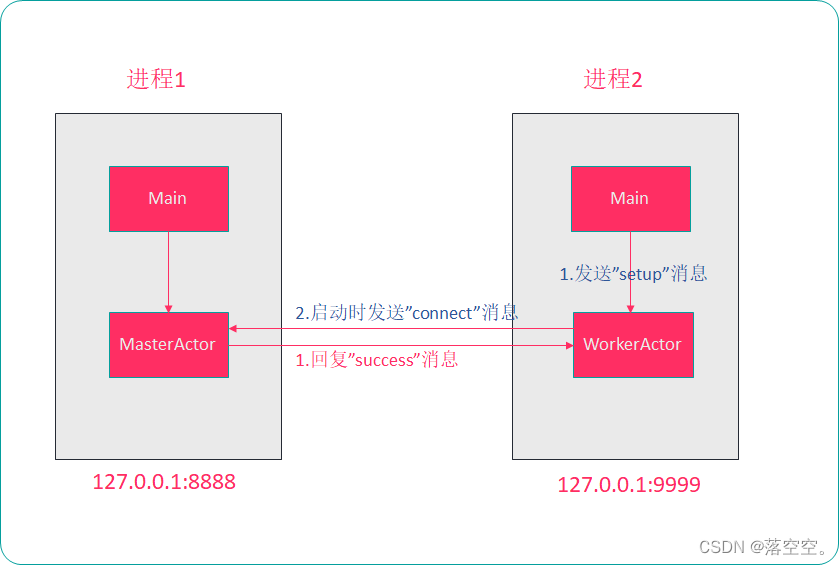
Scala basic tutorial -- 20 -- akka
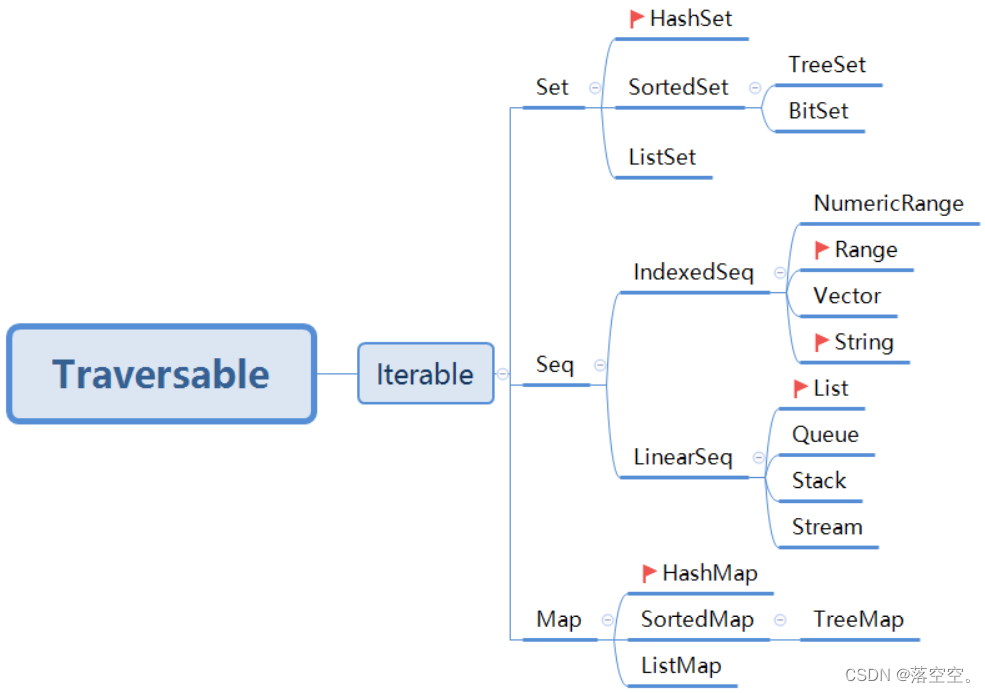
Scala基础教程--17--集合
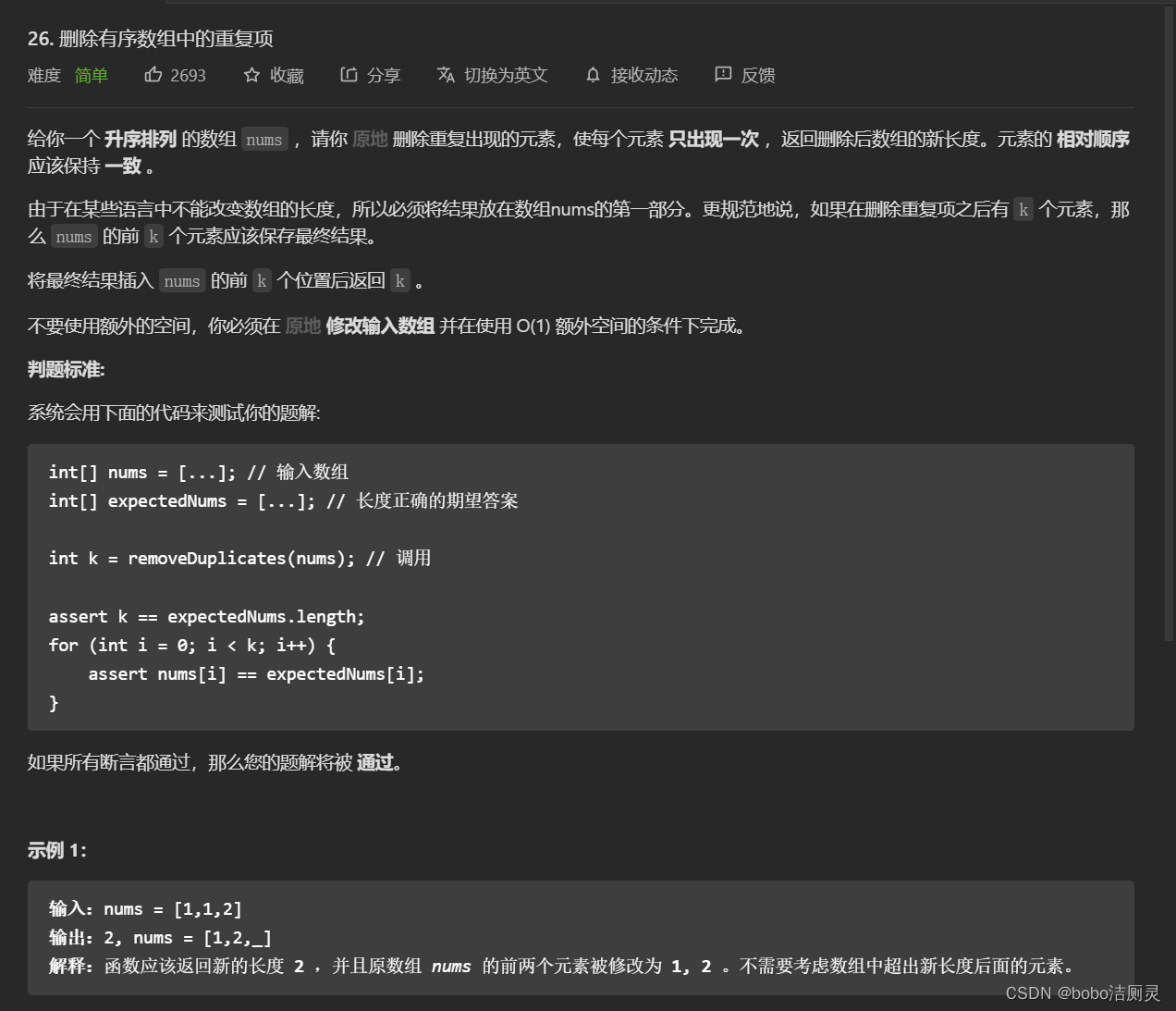
力扣刷題日記/day6/6.28
学习路之PHP--phpstudy创建项目时“hosts文件不存在或被阻止打开”
Unity 制作旋转门 推拉门 柜门 抽屉 点击自动开门效果 开关门自动播放音效 (附带编辑器扩展代码)
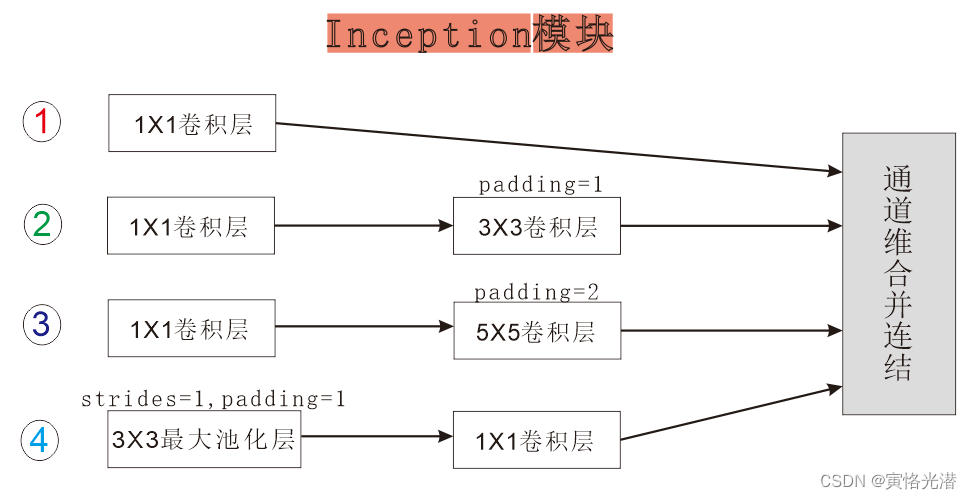
MXNet对GoogLeNet的实现(并行连结网络)
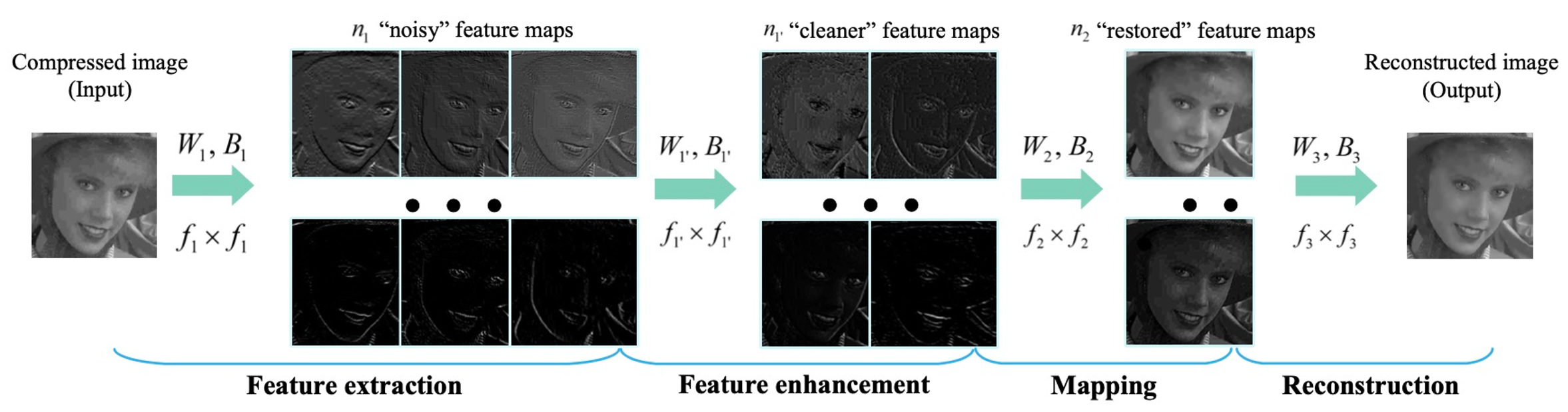
NBA赛事直播超清画质背后:阿里云视频云「窄带高清2.0」技术深度解读
![[HCIA continuous update] WAN technology](/img/31/8e9ed888d22b15eda5ddcda9b8869b.png)
[HCIA continuous update] WAN technology
TorchDrug教程
随机推荐
[cloud voice suggestion collection] cloud store renewal and upgrading: provide effective suggestions, win a large number of code beans, Huawei AI speaker 2!
TorchDrug教程
An example of multi module collaboration based on NCF
Deleting nodes in binary search tree
Load test practice of pingcode performance test
2022 ByteDance daily practice experience (Tiktok)
Digital "new" operation and maintenance of energy industry
Just today, four experts from HSBC gathered to discuss the problems of bank core system transformation, migration and reconstruction
Blue bridge: sympodial plant
力扣刷题日记/day3/2022.6.25
[HCIA continuous update] WAN technology
Lua emmylua annotation details
fopen、fread、fwrite、fseek 的文件处理示例
Journal des problèmes de brosse à boutons de force / day6 / 6.28
Crawler (6) - Web page data parsing (2) | the use of beautifulsoup4 in Crawlers
输入的查询SQL语句,是如何执行的?
Unity 制作旋转门 推拉门 柜门 抽屉 点击自动开门效果 开关门自动播放音效 (附带编辑器扩展代码)
Scala基础教程--13--函数进阶
Angry bird design based on unity
Scala基础教程--12--读写数据