当前位置:网站首页>ShanDong Multi-University Training #3
ShanDong Multi-University Training #3
2022-06-29 12:13:00 【Zqchang】
Catalog
New String
Carelessness
Here you are. 26 Letters , Represents the priority of these letters , And give you some strings , Let you sort these strings according to the given priority , And then output number k A string
Notice the two sorting conditions given in this topic , Come in order
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <map>
#include <string>
#include <cstring>
#include <cmath>
#include <stack>
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define fast ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define sc(a) scanf("%lld",&a)
#define pf(a) printf("%d",a)
#define endl "\n"
#define int long long
#define mem(a,b) memset(a,b,sizeof a)
#define ull unsigned long long
#define INF 0x3f3f3f3f3f3f3f3f
#define inf 0x3f3f3f3f
#define rep(i,a,b) for(auto i=a;i<=b;++i)
#define bep(i,a,b) for(auto i=a;i>=b;--i)
#define LL long long
#define lowbit(x) x&(-x)
#define PII pair<int,int>
#define PLL pair<ll,ll>
#define PI acos(-1)
#define pb push_back
#define x first
#define y second
const double eps = 1e-6;
const int mod = 998244353;
const int MOD = 1e9 + 7;
int n, k;
map<char, int> mp;// Compare the size
string v[1010];
bool cmp(string s1, string s2)
{
int a = s1.size();
int b = s2.size();
for(int i = 0, j = 0; i < a && j < b; i++, j++)
{
if(mp[s1[i]] < mp[s2[j]]) return true;
else if(mp[s1[i]] > mp[s2[j]]) return false;
}
if(a < b)return true;
return false;
}
signed main()
{
fast;
string s;
cin >> s;
for(int i=0; i<26; i++)
{
mp[s[i]] = i;
}
cin >> n;
for(int i = 1; i <= n; i++)
cin >> v[i];
cin >> k;
sort(v + 1, v + n + 1, cmp);
cout << v[k] << endl;
}
/* acbdefghijklmnopqrstuvwxyz 1 abcd 1 */
C - Easy Problem
Easy Problem
It's also a water problem , But I read false questions during the competition , Didn't do it
Carelessness
Just say there are two people , Starting from two positions , They move the same , But if the next step is to exceed or the next step is an obstacle , Just don't move. , Ask you at least a few steps to get together , Or not together
bfs Direct killing
#include<bits/stdc++.h>
using namespace std;
const int N = 55;
char mp[N][N];
int vis[N][N][N][N];
int dist[N][N][N][N];
struct node
{
int xa, ya;
int xb, yb;
};
int n;
int dx[] = {
0, 0, 0, 1, -1};
int dy[] = {
0, 1, -1, 0, 0};
queue<node> q;
bool judge(int x,int y)
{
if(x < 1 || x > n || y < 1 || y > n || mp[x][y]=='*')
return false;
return true;
}
///*
void bfs(int x1, int y1, int x2, int y2)
{
memset(vis, 0x3f, sizeof vis);
q.push({
x1, y1, x2, y2});
vis[x1][y1][x2][y2] = 0;
while(q.size())
{
node t = q.front();
q.pop();
if(t.xa == t.xb && t.ya == t.yb)
{
cout << vis[t.xa][t.ya][t.xb][t.yb] << endl;
return ;
}
for(int i=1; i<=4; i++)
{
int xxa = t.xa + dx[i], yya = t.ya + dy[i], xxb = t.xb + dx[i], yyb = t.yb + dy[i];
if(mp[xxa][yya] == '*' && mp[xxb][yyb] == '*') continue;
if(!judge(xxa, yya)) {
xxa -= dx[i]; yya -= dy[i];}
if(!judge(xxb, yyb)) {
xxb -= dx[i]; yyb -= dy[i];}
if(vis[xxa][yya][xxb][yyb] > vis[t.xa][t.ya][t.xb][t.yb] + 1)
{
vis[xxa][yya][xxb][yyb] = vis[t.xa][t.ya][t.xb][t.yb] + 1;
q.push({
xxa, yya, xxb, yyb});
}
}
}
puts("no solution");
}
//*/
int main()
{
cin >> n;
int x1, y1, x2, y2;
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
{
cin >> mp[i][j];
if(mp[i][j] == 'a') x1 = i, y1 = j;
if(mp[i][j] == 'b') x2 = i, y2 = j;
}
bfs(x1, y1, x2, y2);
return 0;
}
I - 250-like Number
Carelessness
Definition k=p× q 3 q^3 q3 also p and q All prime numbers , In this way k Just like that. 250 Number of numbers , ask n How many such numbers are there within
Good idea , I wanted to use it directly at first pow Open a cube , Then I found that the accuracy error was quite large , In the end, there are not a few less , And then decide , Multiply with n Compare , Is that you sift out prime numbers , enumeration p perhaps q, Then ask , Let me enumerate here q, Because I feel so easy to do
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <map>
#include <string>
#include <cstring>
#include <cmath>
#include <stack>
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define fast ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define sc(a) scanf("%lld",&a)
#define pf(a) printf("%d",a)
#define endl "\n"
#define int long long
#define mem(a,b) memset(a,b,sizeof a)
#define ull unsigned long long
#define INF 0x3f3f3f3f3f3f3f3f
#define inf 0x3f3f3f3f
#define rep(i,a,b) for(auto i=a;i<=b;++i)
#define bep(i,a,b) for(auto i=a;i>=b;--i)
#define LL long long
#define lowbit(x) x&(-x)
#define PII pair<int,int>
#define PLL pair<ll,ll>
#define PI acos(-1)
#define pb push_back
#define x first
#define y second
const double eps = 1e-6;
const int mod = 998244353;
const int MOD = 1e9 + 7;
const int N = 8e6;
int primes[N], cnt; // primes[] Store all primes
bool st[N]; // st[x] Storage x Whether it has been screened out
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) primes[++ cnt] = i;
for (int j = 1; primes[j] <= n / i; j ++ )
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
signed main()
{
int n; cin >> n;
int res = 0;
get_primes(8e6);
for(int i = 1; i <= cnt; i++)
{
int l = 0, r = i - 1;
int nn = primes[i] * primes[i] * primes[i];
if (nn > n) break;
while (l < r)
{
int mid = l + r + 1 >> 1;
if (nn <= n / primes[mid]) l = mid;
else r = mid - 1;
}
res += l;
}
cout << res << endl;
return 0;
}
E - Prefix Equality
The main idea is , Here are two sequences , Here are two numbers for you , Let's see if the set of numbers in the numbers before each sequence is the same , Sets have anisotropy
practice , A small hash , Make each number different and add a piece , Then throw an array and save it
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <map>
#include <string>
#include <cstring>
#include <cmath>
#include <stack>
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define fast ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define sc(a) scanf("%lld",&a)
#define pf(a) printf("%d",a)
#define endl "\n"
#define int long long
#define mem(a,b) memset(a,b,sizeof a)
#define ull unsigned long long
#define INF 0x3f3f3f3f3f3f3f3f
#define inf 0x3f3f3f3f
#define rep(i,a,b) for(auto i=a;i<=b;++i)
#define bep(i,a,b) for(auto i=a;i>=b;--i)
#define LL long long
#define lowbit(x) x&(-x)
#define PII pair<int,int>
#define PLL pair<ll,ll>
#define PI acos(-1)
#define pb push_back
#define x first
#define y second
const double eps = 1e-6;
const int mod = 998244353;
const int MOD = 1e9 + 7;
const int N = 2e5 + 10;
typedef unsigned long long ULL;
int P = 131;
ULL p; // h[k] Before storing the string k A letter hash value , p[k] Storage P^k mod 2^64
ULL a[N], b[N];
set<int> st;
signed main()
{
int n, x; cin >> n;
for (int i = 1; i <= n; i ++ )
{
cin >> x;
if(st.count(x)) a[i] = a[i - 1];
else
{
a[i] = a[i - 1] + x * (x + P);
st.insert(x);
}
}
// cout << endl;
st.clear();
// p = 0;
for (int i = 1; i <= n; i ++ )
{
cin >> x;
if(st.count(x)) b[i] = b[i - 1];
else
{
b[i] = b[i - 1] + x * (x + P);
st.insert(x);
}
}
// puts("");
int m; cin >> m;
int l, r;
while(m --)
{
cin >> l >> r;
if(a[l] == b[r]) puts("Yes");
else puts("No");
}
return 0;
}
K - Endless Walk
It's a conclusion
The main idea of this question is , Let you find the number of good points in the graph , A good definition is that you can start from this point , Go to a ring , Be careful , This graph is a directed graph , Ensure that there are no heavy edges
In fact, it is to create a map in reverse and then run a topological order , As for how to prove , You can think like this , The topology will not go to the ring , Then reverse mapping is to find out the points on the ring that cannot be reached , Subtract these points from all the points
I can't think of a way to draw by myself
Quote from other blogs :
In fact, it's from 1 From point to ring ( Including ring ) All points contained in the path of . We know that when looking for topological sorting, the current penetration is 0 The point of , It can be seen that in the process of finding topology sorting , The ring will never be traversed ( The penetration of the starting point of the ring cannot be 0), At the same time, there are other points that are not on the path from the starting point to the loop and are connected with the loop . So we need to save an inverse graph of the original graph , Find the topological sequence from the starting point of the inverse graph ( In fact, it is no longer a topological sequence in the strict sense , It's just easy to understand. It's called ), Any point that can be traversed , It must not be from the original picture 1 On the path from point No. to the ring , Points that are not traversed , It must be from the original picture 1 On the path from point No. to the ring , That's the answer we asked for .
Link to the original text :https://blog.csdn.net/qq_42883649/article/details/123801622
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define IOS std::ios::sync_with_stdio(false);std::cin.tie(0);
const int N = 2e5 + 10, M = 2e5 + 10;
vector<int> v[N];
int n, m;
int in[N];
int main()
{
// IOS
cin >> n >> m;
int ans = n;
int a, b;
for(int i=1; i<=m; i++)
{
cin >> a >> b;
v[b].push_back(a);
in[a] ++;
}
queue<int> q;
for(int i=1; i<=n; i++)
if(in[i] == 0)
{
q.push(i);
// ans --;
}
while(q.size())
{
ans --;
int t = q.front();
// cout << t << endl;
q.pop();
for(auto i : v[t])
{
in[i] --;
if(in[i] == 0)
{
q.push(i);
// ans --;
}
}
}
cout << ans << endl;
return 0;
}
J - Wrapping Chocolate
Wrapping Chocolate
Here you are. n A chocolate ,m Boxes , Ask if you can put them all in , The box and the width of the chocolate are for you , Make sure the box is equal to or greater than the number of chocolates , Ask you if you can put all the chocolates in
greedy , It is difficult to be greedy from childhood , Then we can change our thinking , From big to small greed , First sort the boxes and chocolates , I'll follow my own code here , It is to sort the box and chocolate in the same order according to their length and width , Then start with the last chocolate , Find the best box for this chocolate , To put it bluntly, I'm looking for something bigger than this chocolate , The smallest box ! How to find it , Two points , You can also use a multiset, To find a box larger than this chocolate , I sort by length here , That is to say , I want to find , All widths greater than or equal to the length of this chocolate , Throw it all in multiset Inside , Then half the length of the chocolate OK 了 , If there is any nonconformity , Because we are looking from big to small , You can directly determine , The length is smaller than it in the future , So we must not put them all in , Just exit
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <map>
#include <string>
#include <cstring>
#include <cmath>
#include <stack>
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define fast ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define sc(a) scanf("%lld",&a)
#define pf(a) printf("%d",a)
#define endl "\n"
#define int long long
#define mem(a,b) memset(a,b,sizeof a)
#define ull unsigned long long
#define INF 0x3f3f3f3f3f3f3f3f
#define inf 0x3f3f3f3f
#define rep(i,a,b) for(auto i=a;i<=b;++i)
#define bep(i,a,b) for(auto i=a;i>=b;--i)
#define LL long long
#define lowbit(x) x&(-x)
#define PII pair<int,int>
#define PLL pair<ll,ll>
#define PI acos(-1)
#define pb push_back
#define x first
#define y second
const double eps = 1e-6;
const int mod = 998244353;
const int MOD = 1e9 + 7;
const int N = 2e5 + 10;
PII a[N], b[N];
int n, m;
multiset<int> s;
bool cmp(PII a, PII b)
{
if(a.x != b.x) return a.x < b.x;
else return a.y < b.y;
}
signed main()
{
// fast;
cin >> n >> m;
for(int i=1; i<=n; i++) cin >> a[i].x;
for(int i=1; i<=n; i++) cin >> a[i].y;
for(int i=1; i<=m; i++) cin >> b[i].x;
for(int i=1; i<=m; i++) cin >> b[i].y;
sort(a + 1, a + 1 + n, cmp);
sort(b + 1, b + 1 + m, cmp);
for(int i=n, j=m; i>=1; i--)
{
while(j >=1 && b[j].x >= a[i].x)
{
s.insert(b[j].y);
j --;
}
auto t = s.lower_bound(a[i].y);
if(t == s.end())
{
puts("No");
return 0;
}
else s.erase(t);
}
puts("Yes");
return 0;
}
G - Optimal Biking Strategy
G - Optimal Biking Strategy
Dynamic programming
Carelessness
Just say a person starts from home to go to a store , There are several bike stops on the way , It can and can only ride at the bicycle station , What is the smallest thing you can walk
standard dp, But how to push , What feels good is , He must ride from the farthest station within the farthest distance of the last station , So we can specify the status f[i][j] Go to the first place i A station , The largest flower j How many roads does yuan need to go
Then how to find the farthest station , Two points, of course
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <map>
#include <string>
#include <cstring>
#include <cmath>
#include <stack>
#include<bitsdc++.h>
using namespace std;
#define ll long long
#define fast ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define sc(a) scanf("%lld",&a)
#define pf(a) printf("%d",a)
#define endl "\n"
#define int long long
#define mem(a,b) memset(a,b,sizeof a)
#define ull unsigned long long
#define INF 0x3f3f3f3f3f3f3f3f
#define inf 0x3f3f3f3f
#define rep(i,a,b) for(auto i=a;i<=b;++i)
#define bep(i,a,b) for(auto i=a;i>=b;--i)
#define LL long long
#define lowbit(x) x&(-x)
#define PII pair<int,int>
#define PLL pair<ll,ll>
#define PI acos(-1)
#define pb push_back
#define x first
#define y second
const double eps = 1e-6;
const int mod = 998244353;
const int MOD = 1e9 + 7;
const int N = 1e6 + 10;
int f[N][10];
int a[N];
int n,p,s,k;
signed main()
{
fast;
cin >> n >> p >> s;
for(int i=1;i<=n;i++) cin >> a[i];
cin >> k;
memset(f, 0x3f, sizeof f);
for(int i=0; i<=k; i++) f[0][i] = 0;// initialization , When at the starting point , How much money did not walk
for(int i=1; i<=n; i++)
{
f[i][0] = f[i-1][0] + a[i] - a[i-1];// At best, just walk over , Just get the biggest one first
for(int j=1; j<=k; j++)// Enumerate how much money there is
{
f[i][j] = f[i-1][j] + a[i] - a[i-1];// At best, just walk over , Just get the biggest one first
for(int x=0; x<=j; x++)// Enumerate how much money you can go
{
int dist = x * s;// Riding distance
int l = 1, r = i - 1;
while(l < r)
{
int mid = (l + r) >> 1;
if(a[i] - a[mid] <= dist) r = mid;
else l = mid + 1;
}// Pay attention here !! There may be a situation where the answer to this dichotomy cannot be found , Therefore, it is necessary to make a special judgment
// When l Greater than r When , Maybe there is no two points at all , You can't be more detailed at this time , such as 1, 0
// If a[i] - a[r] > dist There is no solution at this time , But maybe two points , Also judge that you can't update
if(l <= r && a[i] - a[r] <= dist) f[i][j]=min(f[i][j], f[r][j - x]);
}
}
}
int res = INF;
for(int i=1; i<=n; i++)
res = min(res, f[i][k] + p - a[i]);
cout << res << endl;
return 0;
}
D - Maximum Value
Carelessness
Give you a pile of numbers , Let you find out from these numbers a i a_i ai mod a j a_j aj The maximum of , Guarantee a i a_i ai >= a j a_j aj
If you want to take the largest module , It must be a multiple of the modulus -1 such , So we enumerate multiples , Look at the maximum value smaller than each number multiple , Take a mold , Then take one from the maximum value max, The final answer is , The data is in the range of two points ,2e6 Because the largest number may be 1e6
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <map>
#include <string>
#include <cstring>
#include <cmath>
#include <stack>
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define fast ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define sc(a) scanf("%lld",&a)
#define pf(a) printf("%d",a)
#define endl "\n"
#define int long long
#define mem(a,b) memset(a,b,sizeof a)
#define ull unsigned long long
#define INF 0x3f3f3f3f3f3f3f3f
#define inf 0x3f3f3f3f
#define rep(i,a,b) for(auto i=a;i<=b;++i)
#define bep(i,a,b) for(auto i=a;i>=b;--i)
#define LL long long
#define lowbit(x) x&(-x)
#define PII pair<int,int>
#define PLL pair<ll,ll>
#define PI acos(-1)
#define pb push_back
#define x first
#define y second
const double eps = 1e-6;
const int mod = 998244353;
const int MOD = 1e9 + 7;
vector<int> v; // Store all values to be discretized
int n;
signed main()
{
fast;
cin >> n;
int a;
for(int i=1; i<=n; i++)
{
cin >> a;
v.push_back(a);
}
sort(v.begin(), v.end()); // Sort all values
v.erase(unique(v.begin(), v.end()), v.end()); // Remove the repeating elements
int res = 0;
for(int i=0; i<v.size(); i++)
{
for(int j=v[i] + v[i]; j<=2e6; j+=v[i])
{
int id = lower_bound(v.begin(), v.end(), j) - v.begin() - 1;// The returned subscript is subtracted 1 It is the biggest one smaller than it
if(id == -1) continue;
res = max(res, v[id] % v[i]);
}
}
cout << res << endl;
return 0;
}
边栏推荐
- Pro test! Centos7 deploy PHP + spool
- AOSP ~ Logcat 持久化
- Deep understanding of volatile keyword
- GBase8s数据库INTO table 子句
- GBase8s数据库select有ORDER BY 子句4
- Helping the ultimate experience, best practice of volcano engine edge computing
- &3 在浏览器中查看请求报文和响应报文
- 文件包含之日志中毒(User-Agent)
- 论文复现——AC-FPN:Attention-guided Context Feature Pyramid Network for Object Detection.
- Oracle expands distributed cloud services to bring comprehensive public cloud services to more customers
猜你喜欢
![[pbootcms模板]作文网站/文档下载网站源码](/img/6e/51bbb4ce961defa4abd098ff3af21f.jpg)
[pbootcms模板]作文网站/文档下载网站源码

谷粒商城项目
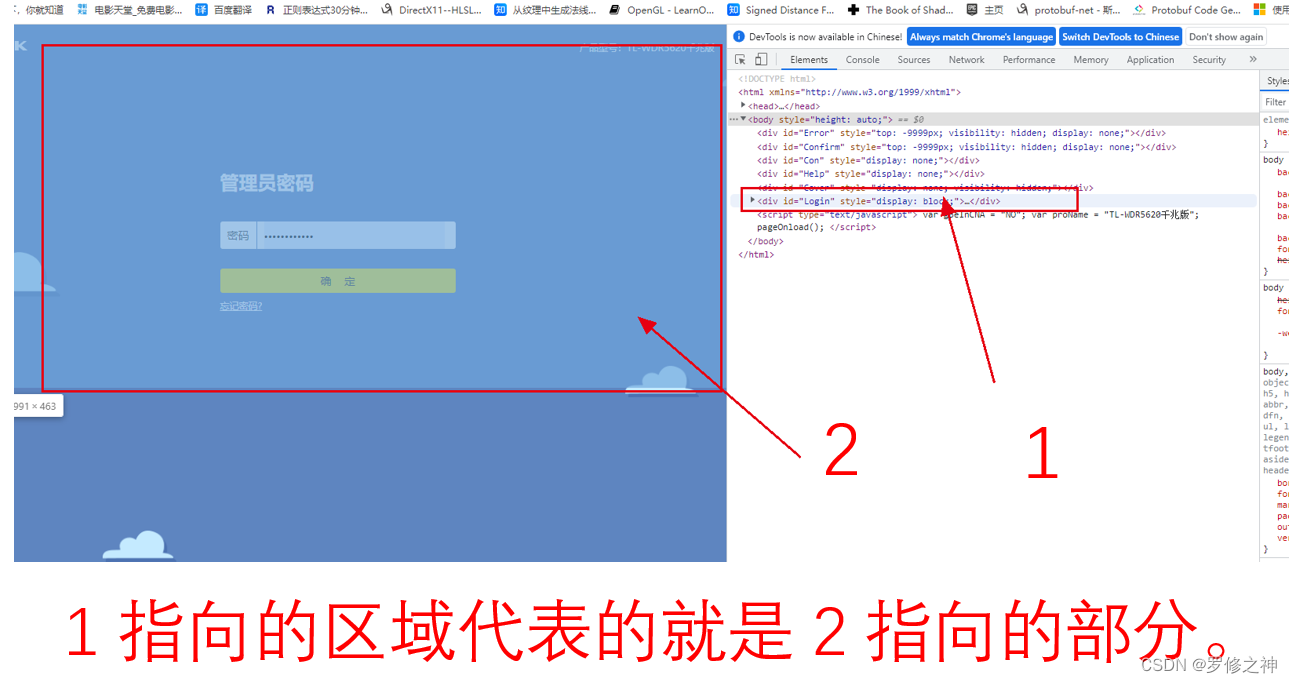
How to view saved passwords of websites

嵌入式数据库开发编程(四)——DDL、DML

RepOptimizer: 其实是RepVGG2

亲测!Centos7部署PHP + Swoole

Embedded database development programming (IV) -- DDL, DML

Imile uses Zadig's multi cloud environment to deploy thousands of times a week to continuously deliver global business across clouds and regions

龙书虎书鲸书啃不动?试试豆瓣评分9.5的猴书
联想领像 lenovoimage 部分打印机 驱动 PPD 文件
随机推荐
杰理之关于 TWS 配对方式配置【篇】
服务数百万开发者,首届 Techo Day 腾讯技术开放日发布 7 款“轻量级”产品
助力极致体验,火山引擎边缘计算最佳实践
MariaDB的安装与配置
RSLO:自监督激光雷达里程计(实时+高精度,ICRA2022)
GBase8s数据库对 STANDARD 或 RAW 结果表排序
AutoCAD - text display mode and how CAD can directly open Tianzheng drawings
Record once MSI notebook ge63 plays webpage video flash screen and randomly turns green to solve the problem
2022广西省安全员C证考试试题及模拟考试
小白学习MySQL - 增量统计SQL的需求 - 开窗函数的方案
Jerry's configuration of TWS cross pairing [chapter]
如何在Rocky Linux和AlmaLinux上安装MySQL 8.0
Windwos10安装sshd服务
Matlab GUI realizes the function of clicking the button, opening the file dialog box and importing pictures
又一所“省会大学”,来了!
TTChat x Zadig 开源共创 Helm 接入场景,环境治理搞得定!
速看|期待已久的2022年广州助理检测工程师真题解析终于出炉
Jerry's initiation of ear pairing, reconnection, and opening of discoverable and connectable cycle functions [chapter]
ONES 创始人王颖奇对话《财富》(中文版):中国有没有优秀的软件?
What is the main account of Chia Tai futures used for 4 quotation software?