浅谈单调栈

什么是单调栈？

• 单调栈实际上就是栈，只是限制要比普通的栈更严格而已了。要求是每次入栈的元素必须要有序（如果新元素入栈不符合要求，则将之前的元素出栈，直到符合要求再入栈），使之形成单调递增/单调递减的一个栈。

比如我们有一个数组：

• 单调递增栈：只有比他小的才直接入栈，如果大于就先出栈再入栈（在出栈的时候可以进行一些操作计算，如求温度那一题就是在出栈时候计算第一个大于该值他们之间的距离）。适用于求解第一个大于该位置元素的数

• 单调递减栈：只有比他大的才入栈，如果小于的话，也是先出栈再入栈。适用于求第一个小于该位置元素的数

• 如何判断是 单调递增/递减栈 是按照出栈的顺序决定的，比如栈为 {1, 2, 6}，出栈后，为{6, 2, 1}，这是递减顺序的，所以就是单调递减栈了

单调栈适合的题目是求解 第一个大于 xxx 或者 第一个小于 xxx 这种题目。当出现类似题目时候应该优先想到使用单调栈来解题。

---

我们来举一个单调递减栈的例子：

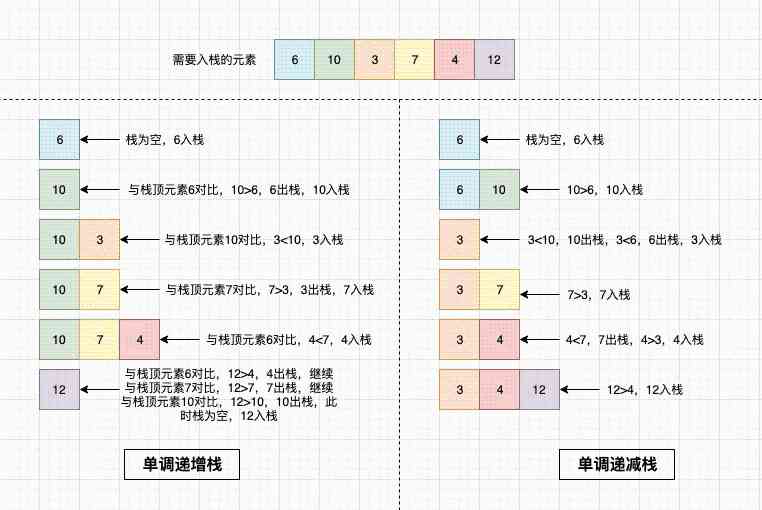
• 比如我们要将数组 {1, 3, 4, 5, 2, 9, 6} 压入栈：

1. 首先1入栈，此时栈为：{1}
2. 接下来是3，由于 3 > 1 ，直接入栈，此时栈为：{1, 3}
3. 接下来是4，由于 4 > 3 ，直接入栈，此时栈为：{1, 3, 4}
4. 接下来是5，由于 4 > 3 ，直接入栈，此时栈为：{1, 3, 4, 5}
5. 接下来是2，因为 2 < 5，不满足条件，所以我们将5出栈，此时栈为：{1, 3, 4}
6. 然后再将2与4比较，因为 2 < 4 ，还是不满足条件，所以再将4出栈，此时栈为：{1, 3}
7. 然后再将2与3比较，因为 2 < 3 ，还是不满足条件，所以再将3出栈，此时栈为：{1}
8. 然后将2与1比较，因为 2 > 1 ，满足条件，将2入栈，此时栈为：{1, 2}
9. 接下来是9，由于 9 > 2 ，直接入栈，此时栈为：{1, 2, 9}
10. 接下来是6，因为 6 < 9 ，不满足条件，将9出栈，此时栈为：{1, 2}
11. 然后6与2比较，6 > 2 ，满足条件，6入栈，此时栈为{1, 2, 6}
12. 最后，目标数组都遍历完了，我们就得到了该结果

---

现在有这样一个题目：

• 给你一个数组，返回一个等长的数组，对应索引存储着下一个更大的元素，如果没有更大的元素，就存-1。这个要怎么解呢？
  • 如果输入的是{2, 1, 2, 4, 3}，那么我们会得到结果{4, 2, 4, -1, -1}
  • 这个结果是怎么得来的捏？向右扫描，比2大的第一个数是4，比1大的第一个数是2，没有比4大的数(4 > 3)，也没有比3大的数(3 == 3)，所以这两个为-1

可以尝试一下做下这一题：739. 每日温度

经过多次做题总结，不难发现，其实是有套路模板的，以后做题只需要修改一些即可：

class Solution {
    public int[] monotonousStack(int[] T) {
        LinkedList<Integer> stack = new LinkedList<>();
        // 用来存放第一个大于该位置元素的距离
        int[] res = new int[T.length];

        for (int i = 0; i < T.length; i++) {
            while (!stack.isEmpty() && T[i] > T[stack.peek()]) {
                int peek = stack.pop();
                // i - peek 是求解在peek的右边中，第一个大于T[peek]的元素
                res[peek] = i - peek;
            }
            stack.push(i);
        }
        return res;
    }
}

「复杂度分析」

• 时间复杂度：由于数组的元素最多只会入栈，出栈一次，因此时间复杂度仍然是\(O(N)\) ，其中 N 为数组长度
• 空间复杂度：由于使用了栈， 并且栈的长度最大是和数组长度一致，因此空间复杂度是 \(O(N)\)，其中 N 为数组长度

对于有些时候，如果会用到数组的全部元素，即栈中的元素最后都要出栈，那么很可能因为没有考虑边界而无法通过。所以我们可以使用 哨兵法 ，在 {1, 3, 4, 5, 2, 9, 6} 末尾添加一个 -1 作为哨兵，变成了 {1, 3, 4, 5, 2, 9, 6, -1} ，这种技巧可以简化代码逻辑。