当前位置:网站首页>Hdu3117 Fibonacci numbers [mathematics]
Hdu3117 Fibonacci numbers [mathematics]
2022-07-27 14:56:00 【51CTO】
Topic link :
http://acm.hdu.edu.cn/showproblem.php?pid=3117
The main idea of the topic :
Give you an integer N(0 <= N <= 10^8), Find Fibonacci number number number number number number N term F[N] The first four digits and the last four digits of .
Ideas :
Fibonacci sequence is a big number , Direct violence enumeration is obviously unscientific . Consider the end first 4 Whether the bit has a cyclic section , Write a
The program found that the loop section is 15000, Directly use the array to store the front 15000 At the end of the Fibonacci sequence of 4 position . As for Fibonacci
Before the sequence 4 position . It is calculated that N >= 40 after ,F[N] Greater than 8 Number of digits . about N < 40 The part of can be directly
Output results , about N >= 40 Part of , Consider the formula F[N] =(1/√5) * ( ((1+√5)/2)^n - ((1-√5)/2)^n ).
set up F[N] Can be expressed as t * 10^k(t Is a decimal ), So right. F[N] = t * 10^k Take logarithms on both sides log10, obtain :
log10(F[N]) = log10(t) + k .log10(t) = log10(F[N]) - k, because t It must be less than 10 Decimals of , therefore ,
log10(t) < 1, and k Integers , that log10(t) The value is log10(F[N]) Remove the decimal part of the integer part .
use pow(10.0,log10(t)) Find out t. take t*1000 Take the integer part and you get F[N] Before 4 position .
And a little bit more , seek F[N] = (1/√5) * ( ((1+√5)/2)^n - ((1-√5)/2)^n ) When , because N>=40 When ,
((1-√5)/2)^n It is already a very small decimal ( After the decimal point 10 Bit left and right ), So you can directly ignore . It looks like ,
F[N] ≈ (1/√5) * ((1+√5)/2)^n.log10(F[N]) Simplify :1/sqrt(5.0) + N*log10(1+(sqrt(5.0))/2.0).
AC Code :
边栏推荐
- Detailed explanation of Telnet remote login AAA mode [Huawei ENSP]
- C language layered understanding (C language array)
- OBS 进阶之 DXGI 采集屏幕流程,并如何修改为自己的光标
- [popular science] the difference and connection between accuracy and resolution
- < C> C language hash table usage
- watch VS watchEffect
- 汉字风格迁移篇---对抗性区分域适应(L1)Adversarial Discriminative Domain Adaptation
- 【STM32】EXTI
- 【STM32】EXTI
- Nokia's patent business was hit for the first time, and Chinese enterprises are not so easy to knead
猜你喜欢

Interprocess communication

如果我们是那晚负责修复 B 站崩了的开发人员

Who can't capture packets these days? Wireshark packet capture and common protocol analysis are for you!
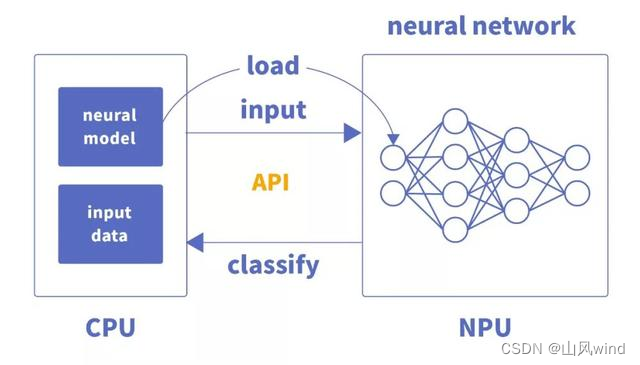
Differences among CPU, GPU and NPU

Summary of basic knowledge of C language

Document translation__ Salt and pepper image denoising based on adaptive total variation L1 regularization

Chinese character style transfer --- antagonistic discriminative domain adaptation (L1)
Database storage series (1) column storage

Ten thousand words detailed Google play online application standard package format AAB
视觉系统设计实例(halcon-winform)-10.PLC通讯
随机推荐
终于有人把面试必考的动态规划、链表、二叉树、字符串全部撸完了
C语言基础知识梳理总结
Simple encapsulation steps of request data request of uniapp
Visual system design example (Halcon WinForm) -10. PLC communication
Slam overview Reading Note 4: a survey on deep learning for localization and mapping: towards the age of spatial 2020
TXT把换行 替换为空格或者取消换行
Win11壁纸变黑怎么办?Win11壁纸变黑了的解决方法
力扣SQL语句习题,错题记录
Unity3d learning note 10 - texture array
Docker practical experience: deploy mysql8 master-slave replication on docker
JS epidemic at home, learning can't stop, 7000 word long text to help you thoroughly understand the prototype and prototype chain
通过VN1630/VN7640的I/O功能来确认电源设置电压的时间精确度
DVWA full level customs clearance tutorial
The interviewer asked: how to judge whether an element is in the visible area?
文献翻译__tvreg v2:用于去噪、反卷积、修复和分割的变分成像方法(部分)
How to help enterprises optimize office management
JS什么是声明提前?函数与变量声明提前的先后顺序(执行上下文铺垫篇)
Detoxify! After Harbin Institute of technology was disabled MATLAB, domestic industrial software fought back domineering
DXGI acquisition process
Document translation__ Tvreg V2: variational imaging method for denoising, deconvolution, repair and segmentation (part)
