当前位置:网站首页>舍不得花钱买1stOpt,不妨试试这款免费的拟合优化神器【openLU】
舍不得花钱买1stOpt,不妨试试这款免费的拟合优化神器【openLU】
2022-08-04 05:35:00 【懂科研的程序员】
想必小伙伴们对1stOpt这款领先世界、当今最强大、最易于使用的国产数值优化分析计算软件平台并不陌生,但与此同时大家也知道它是一款商业软件。虽然网上能够找到其早期的1.5破姐版,但目前最新版已到9.0了。虽然1stOpt对学生用户提供5折优惠,但如果要买完整功能版的得需要花上好几千。可能几百块钱小伙伴们咬咬牙估计也能接受,但几千可能还是要权衡一下。
作为一向爱在各种社区、论坛闲逛的咱自然也会留意一些与1stOpt类似的产品。果不其然,在一次偶然的机会在小木虫上见到一位虫友在1stOpt话题下用一种我不曾见过的语言回答了该问题,而此语言的简洁程度和1stOpt不相上下。按图索骥,最终爬到了www.forcal.net。在此网站上花了一下午的时间把整个语言设计都给学了一遍,给我的整体感觉就是非常容易上手,在一定程度上可作为1stOpt的替代品来使用。
咱所讲的这款神器的名字就叫OpenLU,它是由软件作者采用C/C++开发并维护升级的开放式的数值计算程序,支持所有C/C++的运算符、可自定义函数与计算模块、具有极强的扩展性(加载Lu扩展动态库可实现对Delphi、Fortran等高级语言的交互应用)、能够轻松求解非线性方程(组)、多元积分、微分方程求解、参数优化拟合等各种数学计算与工程计算。

openLU软件界面
作为一款专门的数值计算程序,其使用方法显然不是三言两语就能讲明白的,这里为了让小伙伴们直观感受openLU的强大之处,从其官网(www.forcal.net)摘抄了几个案例供诸君观摩(注:以下示例及相关资源全部来源与官网,对软件作者深表感谢!):
示例1:解含参变量多重积分的方程组

示例1源代码
!!!using["luopt","math"];
init(::p,q,m,C1,C2,C3,C4,k,g,T3,T2)= p=0.020,q=0.219,m=10369.6,C1=800,C2=2,C3=6,C4=8,k=3,g=4,T3=8.0,T2=12.0;
t_T2(u:a:p,q,m)= a=exp[-(p+q)*u],m*p*(p+q)^2*a/(p+q*a)^2;
t2_T2(t::T2,p,q,g)= gsl_qng[@t_T2,t,T2]/[g*(p+q)];
f(t2,T1,y1,y2:a,b:p,q,m,C1,C2,C3,C4,k,g,T3,T2)=
{
a=exp[-(p+q)*T3], b=m*p*(p+q)^2*a/(p+q*a)^2,
y1=-C2*gsl_qng[@t2_T2,t2,T2]+C4*b*[1-k*(p+q)] + C3*{k*(p+q)*gsl_qng[@t_T2,T1,T3]+b*k*(p+q)*t2-k*(p+q)*T3},
y2=C2*T1*T1/[2*g*(p+q)]-k*(p+q)*C3*(t2-T1)-C4*[1-k*(p+q)]
};
Find[@f];示例1结果
结果(每行前面的数是解,最后一个数是误差,下同):
5.689190853227517 3.401756081214042 2.744521617779239e-013
5.03232442248394 -7.261112001867591 2.985639533910636e-012
24.37808017711167 8.27093826714037 3.74498453245254e-012
27.67021280221615 -13.01959458323637 1.01804795021056e-012
145373.6775289801 -775.2875381451365 4.636153342260031e-007
5示例2:缺少部分参数的微分方程拟合
微分方程组如下:
dx/dt=a*x-b*x*y
dy/dt=-c*y+d*x*y
求参数a,b,c,d以及x,y的初值。
数据如下:
t x(t) y(t)
11 45.79 41.40
12 53.03 38.90
13 64.05 36.78
14 75.40 36.04
15 90.36 33.78
16 107.14 35.40
17 127.79 34.68
18 150.77 36.61
19 179.65 37.71
20 211.82 41.98
21 249.91 45.72
22 291.31 53.10
23 334.95 65.44
24 380.67 83.00
25 420.28 108.74
26 445.56 150.01
27 447.63 205.61
28 414.04 281.60
29 347.04 364.56
30 265.33 440.30
31 187.57 489.68
32 128.00 512.95
33 85.25 510.01
34 57.17 491.06
35 39.96 462.22
36 29.22 430.15
37 22.30 396.95
38 16.52 364.87
39 14.41 333.16
40 11.58 304.97
41 10.41 277.73
42 10.17 253.16
43 7.86 229.66
44 9.23 209.53
45 8.22 190.07
46 8.76 173.58
47 7.90 156.40
48 8.38 143.05
49 9.53 130.75
50 9.33 117.49
51 9.72 108.16
52 10.55 98.08
53 13.05 88.91
54 13.58 82.28
55 16.31 75.42
56 17.75 69.58
57 20.11 62.58
58 23.98 59.22
59 28.51 54.91
60 31.61 49.79
61 37.13 45.94
62 45.06 43.41
63 53.40 41.30
64 62.39 40.28
65 72.89 37.71
66 86.92 36.58
67 103.32 36.98
68 121.70 36.65
69 144.86 37.87
70 171.92 39.63
71 202.51 42.97
72 237.69 46.95
73 276.77 54.93
74 319.76 64.61
75 362.05 81.28
76 400.11 105.50
77 427.79 143.03
78 434.56 192.45
79 410.31 260.84
80 354.18 339.39
81 278.49 413.79
82 203.72 466.94
83 141.06 494.72
84 95.08 499.37
85 66.76 484.58
86 45.41 460.63
87 33.13 429.79
88 25.89 398.77
89 20.51 366.49
90 17.11 336.56
91 12.69 306.39
92 11.76 279.53
93 11.22 254.95
94 10.29 233.50
95 8.82 212.74
96 9.51 193.61
97 8.69 175.01
98 9.53 160.59
99 8.68 146.12
100 10.82 131.85
示例2源代码
!!!using["luopt","math"]; //使用命名空间
f(t,x,y,dx,dy, params :: a,b,c,d)=
{
dx = a*x-b*x*y,
dy = -c*y+d*x*y,
0 //必须返回0
};
目标函数(_a,_b,_c,_d,x0,y0 : i,s,ty : tyArray,tA,max, a,b,c,d)=
{
a=_a, b=_b, c=_c, d=_d, //传递优化变量
//最后一个参数50表示gsl_ode函数在计算时,最多循环计算50次,这样可以提高速度
ty=gsl_ode[@f,nil,0.0,tA,ra1(x0, y0), 1e-6, 1e-6, gsl_rk4, 1e-6,50],
i=0, s=0, while{++i<max, s=s+[ty(i,1)-tyArray(i,1)]^2+[ty(i,2)-tyArray(i,2)]^2},
s
};
main(::tyArray,tA,max)=
{
tyArray=matrix{ //存放实验数据ti,xi,yi
"0 0 0 //补充t=0时的数据,拟合时后面的两个0被忽略
11 45.79 41.40
... ...省略数据
100 10.82 131.85"
},
len[tyArray,0,&max], tA=tyArray(all:0), //用len函数取矩阵的行数,tA取矩阵的列
Opt1[@目标函数, optwaygrow] //Opt1函数全局优化
};示例2结果
结果:
0.2146380490718624 1.207150888688551e-003 0.1032935041696845 9.484393405386229e-004 10.66928857150351 104.905115896753 1283.613374197572
(图像来源: forcal.net/yyhz/luoptother.htm)
示例3:复数拟合:利用cole-cole模型拟合介电常数
e=(a+(b-a)/(1+(2*pi*f*c)^2))-1.0i*(d/(2*pi*f*(1/(36*pi)*1e-9))+((b-a)*2*pi*f*c)/(1+(2*pi*f*c)^2))
拟合参数:a,b,c,d
数据:复数 e = e1 + e2 * i (i为虚数单位)
f e1[realPart] e2[imagPart]
20000000 78.6416 0.0101
20718771.93 78.5189 0.0451
21437543.86 78.5453 0.0435
22156315.78 78.587 0.023
22875087.71 78.6542 0.1911
23593859.64 78.6054 0.1855
24312631.57 78.6201 0.1524
25031403.49 78.5626 0.089
25750175.42 78.5386 0.068
26468947.35 78.5829 0.1993
27187719.28 78.6149 0.1347
27906491.2 78.6495 0.2324
28625263.13 78.6226 0.1863
29344035.06 78.5616 0.1389
30062806.99 78.5146 0.0626
30781578.91 78.5795 0.0778
31500350.84 78.5842 0.15
32219122.77 78.5785 0.1944
32937894.7 78.6011 0.1988
33656666.62 78.5833 0.2089
34375438.55 78.5298 0.1492
35610843.56 78.5337 0.1835
36846248.57 78.5676 0.2353
38081653.59 78.5411 0.2025
39317058.6 78.5219 0.209
40552463.61 78.5208 0.2245
41787868.62 78.5198 0.2761
43023273.63 78.5312 0.2217
44258678.64 78.5029 0.2126
45494083.66 78.5344 0.2328
46729488.67 78.5319 0.224
47964893.68 78.5077 0.2183
49200298.69 78.5345 0.2317
50435703.7 78.4988 0.2495
51671108.71 78.5091 0.2274
52906513.72 78.4915 0.2267
54141918.74 78.4901 0.249
55377323.75 78.5024 0.2342
56612728.76 78.4836 0.2522
57848133.77 78.4873 0.2532
59083538.78 78.4978 0.2615
61206918.23 78.4948 0.271
63330297.69 78.4762 0.2821
65453677.14 78.479 0.28
67577056.59 78.4771 0.2963
69700436.05 78.4804 0.2938
71823815.5 78.4822 0.3015
73947194.95 78.486 0.3105
76070574.4 78.482 0.319
78193953.86 78.4746 0.3237
80317333.31 78.4806 0.3389
82440712.76 78.4747 0.3411
84564092.22 78.4703 0.3535
86687471.67 78.4737 0.3644
88810851.12 78.4658 0.3889
90934230.58 78.4736 0.3944
93057610.03 78.482 0.4014
95180989.48 78.4542 0.4141
97304368.93 78.4759 0.416
99427748.39 78.4894 0.4195
101551127.8 78.491 0.4132
105200732.8 78.4802 0.4335
108850337.8 78.4632 0.4587
112499942.8 78.4881 0.4779
116149547.8 78.4726 0.5065
119799152.8 78.4908 0.5164
123448757.8 78.4856 0.5224
127098362.8 78.492 0.5305
130747967.8 78.4948 0.5082
134397572.8 78.5064 0.5592
138047177.8 78.4726 0.5863
141696782.8 78.478 0.5951
145346387.8 78.4849 0.5928
148995992.8 78.4968 0.6001
152645597.8 78.4783 0.5992
156295202.8 78.4736 0.6006
159944807.8 78.4737 0.6351
163594412.8 78.4618 0.652
167244017.8 78.4684 0.6446
170893622.8 78.4699 0.6806
174543227.7 78.4661 0.686
180816066.4 78.479 0.7161
187088905 78.4725 0.7234
193361743.6 78.4698 0.7509
199634582.2 78.4618 0.7711
205907420.8 78.4567 0.7959
212180259.4 78.457 0.8197
218453098 78.4535 0.8434
224725936.6 78.4542 0.8728
230998775.3 78.4548 0.8929
237271613.9 78.4428 0.9265
243544452.5 78.4528 0.9455
249817291.1 78.4494 0.9737
256090129.7 78.4509 0.9944
262362968.3 78.451 1.0089
268635806.9 78.4428 1.0312
274908645.5 78.446 1.0494
281181484.2 78.4415 1.0718
287454322.8 78.4424 1.101
293727161.4 78.4476 1.123
300000000 78.4461 1.1537
310781578.9 78.4525 1.1918
321563157.8 78.4471 1.2336
332344736.7 78.4527 1.2755
343126315.7 78.4449 1.3167
353907894.6 78.4407 1.3568
364689473.5 78.4349 1.4022
375471052.4 78.4317 1.4425
386252631.3 78.4325 1.4809
397034210.2 78.4263 1.5171
407815789.1 78.4243 1.5621
418597368.1 78.4242 1.6133
429378947 78.4334 1.6376
440160525.9 78.4304 1.6946
450942104.8 78.4303 1.7297
461723683.7 78.4214 1.7644
472505262.6 78.4189 1.8087
483286841.5 78.4175 1.8453
494068420.4 78.4149 1.8888
504849999.4 78.4115 1.9302
515631578.3 78.4059 1.9722
534162653.4 78.3997 2.0431
552693728.6 78.3949 2.1094
571224803.8 78.3907 2.1788
589755879 78.391 2.2449
608286954.1 78.3883 2.3201
626818029.3 78.3852 2.3927
645349104.5 78.38 2.4643
663880179.7 78.3711 2.5338
682411254.8 78.3642 2.6052
700942330 78.3575 2.6762
719473405.2 78.3524 2.7449
738004480.3 78.3515 2.8165
756535555.5 78.3502 2.8895
775066630.7 78.3433 2.9579
793597705.9 78.3361 3.0293
812128781 78.3288 3.0984
830659856.2 78.3219 3.1682
849190931.4 78.3161 3.2349
867722006.5 78.3078 3.304
886253081.7 78.3039 3.3728
918103773.5 78.2928 3.4979
949954465.3 78.2817 3.625
981805157.1 78.2674 3.7441
1013655849 78.2551 3.8599
1045506541 78.2436 3.9782
1077357232 78.2297 4.1022
1109207924 78.2163 4.229
1141058616 78.2042 4.3487
1172909308 78.1894 4.4612
1204760000 78.1752 4.5803
1236610691 78.1562 4.7061
1268461383 78.1413 4.832
1300312075 78.1275 4.947
1332162767 78.1113 5.0617
1364013459 78.0944 5.1861
1395864150 78.0747 5.3089
1427714842 78.0588 5.4322
1459565534 78.0435 5.5502
1491416226 78.0232 5.6666
1523266918 78.0036 5.788
1578010993 77.9694 5.9989
1632755067 77.9384 6.1999
1687499142 77.9009 6.4073
1742243217 77.8615 6.6087
1796987292 77.8266 6.8135
1851731367 77.7883 7.0213
1906475442 77.744 7.2225
1961219517 77.7061 7.4315
2015963592 77.6628 7.6281
2070707667 77.6176 7.8345
2125451742 77.5775 8.0377
2180195817 77.531 8.2393
2234939892 77.4807 8.4404
2289683967 77.4391 8.6434
2344428042 77.3859 8.841
2399172116 77.3332 9.0447
2453916191 77.2872 9.2392
2508660266 77.23 9.4387
2563404341 77.1786 9.6421
2618148416 77.1261 9.8366
2712240995 77.0262 10.1777
2806333575 76.9288 10.5137
2900426154 76.8265 10.8515
2994518733 76.7183 11.1866
3088611312 76.6111 11.5187
3182703891 76.4991 11.8533
3276796471 76.3844 12.1827
3370889050 76.2637 12.5094
3464981629 76.1481 12.8349
3559074208 76.0205 13.1668
3653166787 75.8923 13.4861
3747259366 75.7675 13.8109
3841351946 75.632 14.1324
3935444525 75.4994 14.4493
4029537104 75.3629 14.7689
4123629683 75.2199 15.0811
4217722262 75.0831 15.3966
4311814842 74.9318 15.7106
4405907421 74.7874 16.018
4500000000 74.6375 16.3285
示例3源代码
!!!using["luopt","math","win"]; //使用命名空间
g(a,b,c,d,f)= (a+(b-a)/(1+(2*pi*f*c)^2))-1.0i*(d/(2*pi*f*(1/(36*pi)*1e-9))+((b-a)*2*pi*f*c)/(1+(2*pi*f*c)^2));
目标函数(a,b,c,d : i,s, e11,e22 : max, f, e1, e2)=
{
i=-1, s=0, while{++i<max, toreal[g(a,b,c,d,f(i,0)), &e11,&e22], s=s+[e1(i,0)-e11]^2+[e2(i,0)-e22]^2 },
s
};
main(: tArray : max, f, e1, e2)=
{
tArray=matrix{ //存放实验数据 //f e1[realPart] e2[imagPart]
"20000000 78.6416 0.0101
// 省略数据
4500000000 74.6375 16.3285"
},
len[tArray,0,&max], f=tArray(all:0), e1=tArray(all:1),e2=tArray(all:2), //用len函数取矩阵的行数,f等取矩阵的列
Opt1[@目标函数] //Opt1函数全局优化
};示例3结果
结果(a,b,c,d,最小值):
5.918198522529668 78.489752592936 -8.397205875077787e-012 -6.746825318924285e-005 0.4566408877616998
(图像来源: forcal.net/yyhz/luoptother.htm)
由于篇幅原因,更多更复杂、精彩、多样与有用的openLU应用案例就不在此分享了,感兴趣的伙伴欢迎转战www.forcal.net学个痛快。反正咱看完所有案例就有个感觉,学习中遇到的百分之七八十的问题都可以通过案例改改巴拉巴拉就完事,非常方便。
虽然openLU不收大家一分钱,但如果大家在学术活动中获益于openLU的计算结果,不妨显著的标注出来,包括但不限于注明软件来源网站及作者、引用软件作者关于lu以及openLU相关的学术文章。
这里就不分享openLU的软件包了,大家直接点击左下角阅读原文去其官方下载,或直接在浏览器中输入www.forcal.net访问下载。
最后,衷心感谢软件作者开发出如此优秀的数值计算工具并开源其绝大部分源代码,并免费提供给大家使用!
参考资料:www.forcal.net
如需转载,请在公众号中回复“转载”获取授权!
边栏推荐
- 树莓派 4 B 拨动开关控制风扇 Rasberry Pi 4 B Add Toggle Switch for the Fan
- 把DocumentsandSettings迁移到别的盘
- Jackson 使用样例
- DOM的12中节点类型,通过关系或方法获取DOM节点,渲染到浏览器页面的一些特效功能,获取DOM节点来改变属性,点击图片,切换为所点击的图片为背景图,页面上的表单验证,点击底部导航栏切换界面
- 注册表设置默认浏览器 win7,winserver 2008,winserver 2012
- 解决腾讯云DescribeInstances api查询20条记录以上的问题
- Memory Management
- Implementation of ICEEMDAN Decomposition Code in MATLAB
- 关于gopher协议的ssrf攻击
- 水平垂直居中的12种方法,任意插入节点的方法,事件的绑定的三种方法和解绑的方法,事件对象,盒子模型
猜你喜欢

Network skills: teach you to install batteries on the router, you can still surf the Internet when the power is cut off!

Scheduler (Long-term,Short-term, Medium-term Scheduler) & Dispatcher

电脑知识:台式电脑应该选择品牌和组装,值得收藏
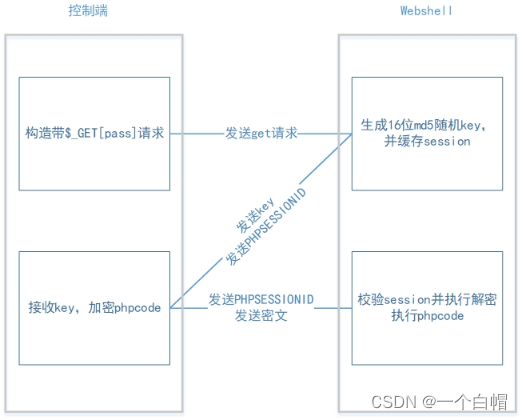
冰歇webshell初探

HbuilderX 启动微信小程序 无法打开项目
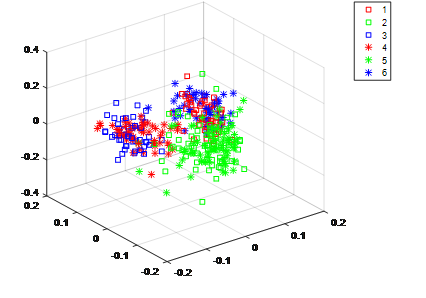
无监督特征对齐的迁移学习理论框架
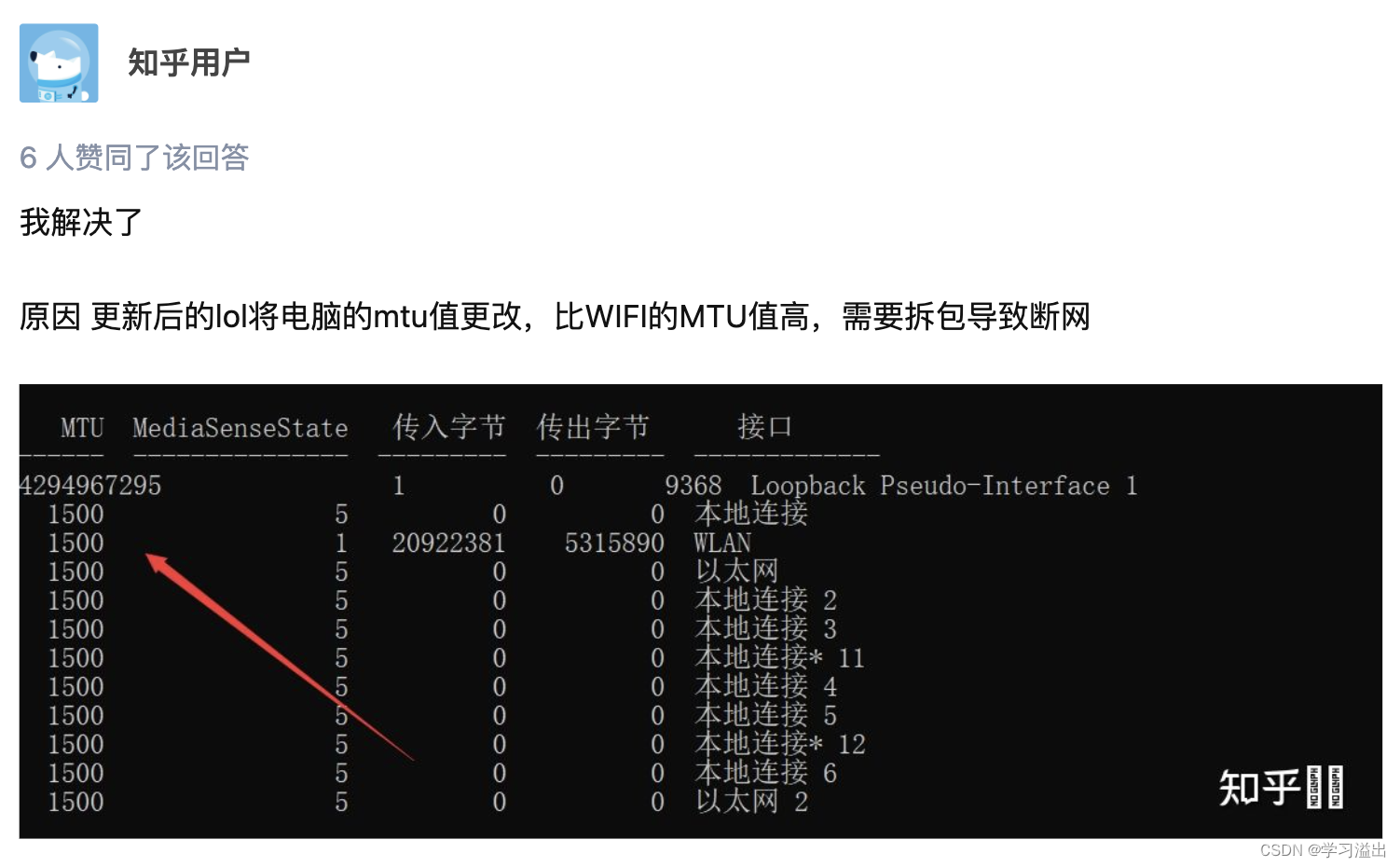
华硕飞行堡垒系列无线网经常显示“无法连接网络” || 一打开游戏就断网

用chrome dev tools 强制js注入
MySQL(4)
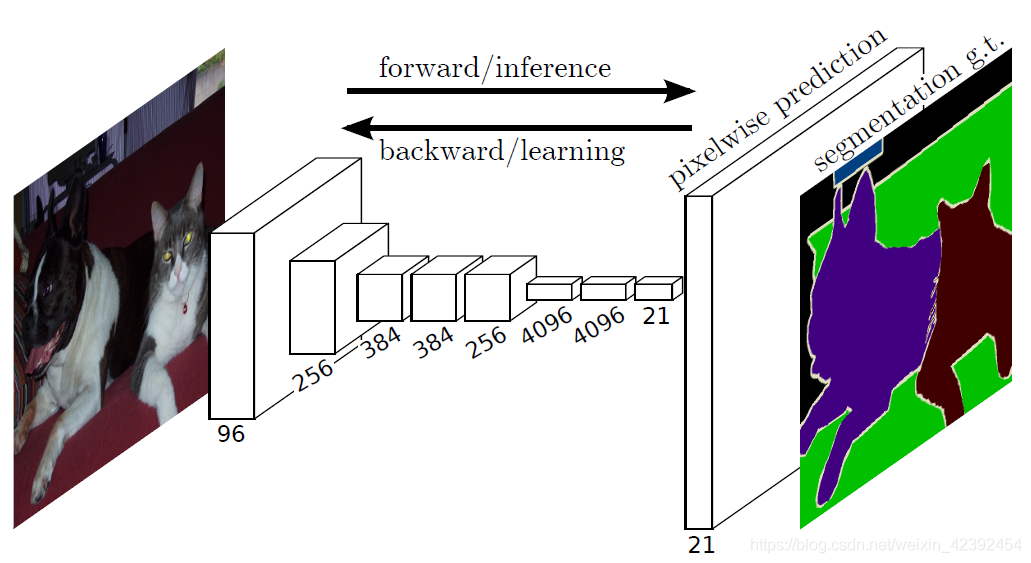
FCN——语义分割的开山鼻祖(基于tf-Kersa复现代码)
随机推荐
IoU, GIoU, DIoU and CIoU in target detection
Uos统信系统 IP地址以及完整主机名配置
如何在网页标题栏中加入图片!
把DocumentsandSettings迁移到别的盘
DOM的12中节点类型,通过关系或方法获取DOM节点,渲染到浏览器页面的一些特效功能,获取DOM节点来改变属性,点击图片,切换为所点击的图片为背景图,页面上的表单验证,点击底部导航栏切换界面
SENet detailed explanation and Keras reproduction code
【音视频开发系列】QT 采集麦克风PCM并播放
杰哥带大家做一次meterpreter内网渗透模拟
ResNet详解:ResNet到底在解决什么问题?
原型图总结规范
Database document generation tool V1.0
C#找系统文件夹路径
冰歇webshell初探
数据库文档生成工具V1.0
数组的一些方法
ES6新语法:symbol,map容器
nacos 返回 403 unknown user 太他么坑了 源码解析
Hardware Knowledge: Introduction to RTMP and RTSP Traditional Streaming Protocols
狗都能看懂的CenterNet讲解及代码复现
读取JDBC配置文件