当前位置:网站首页>二叉树遍历之后序遍历(非递归、递归)入门详解
二叉树遍历之后序遍历(非递归、递归)入门详解
2022-08-02 14:10:00 【杨老头软工】
一、引言
二叉树的遍历常见的方法有先序遍历、中序遍历、后序遍历和层次遍历等,本文给出了C语言版本的后序遍历二叉树的非递归算法和递归算法。
后序遍历不如先序遍历简单,是相对最复杂的一种遍历方法。访问结点的次序是:“左—>右—>根”,也就是首先访问左子树,之后访问右子树,最后访问树根。对于左、右子树而言,其访问的次序依然是“左—>右—>根”。也就是说,对于每一棵子树,都是最后访问树根。
从上面描述可以看出遍历过程其实是递归的过程,因此可以使用递归算法来实现,但是同样也可以使用非递归的方法来实现。
二、二叉树的后序遍历详细演示过程
1、假设二叉树(左右子树全)如下图所示: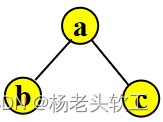
则后序遍历过程是:左子树b—>右子树c—>树根a
2、假设二叉树(没有右子树)如下图所示:
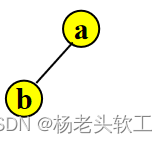
则后序遍历过程是:左子树b—>树根a
3、假设二叉树(没有左子树)如下图所示: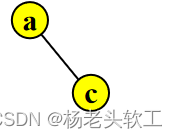
则后序遍历过程是:右子树c—>树根a
4、对于稍微复杂一点的二叉树,如下图所示: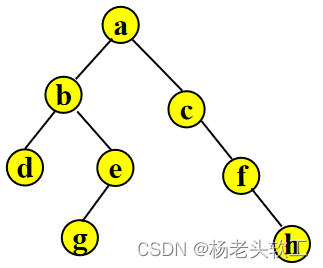
其后序遍历过程演示如下(“左—>右—>根”)
Step 1. 首先访问结点 d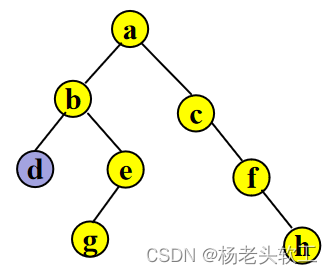
Step 2. 访问结点 g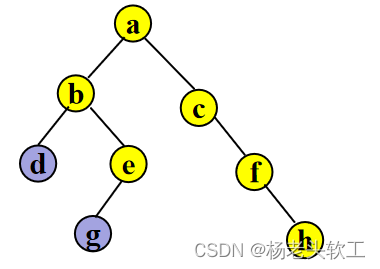
Step 3. 访问结点 e
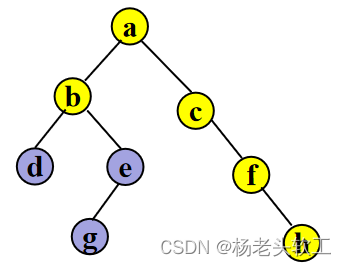
Step 4. 访问结点b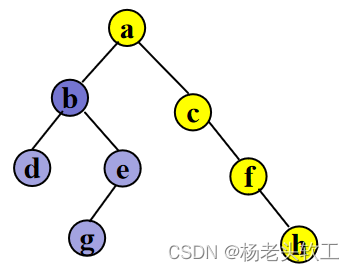
Step 5. 访问结点h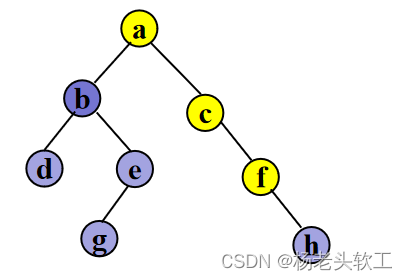
Step 6. 访问结点f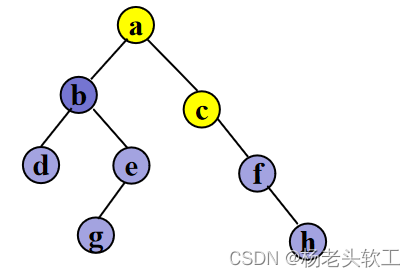
Step 7. 访问结点c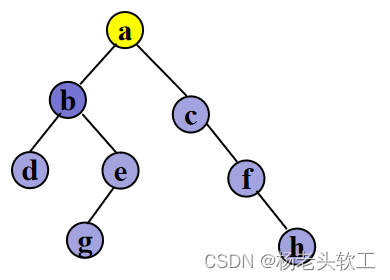
Step 8. 访问树根a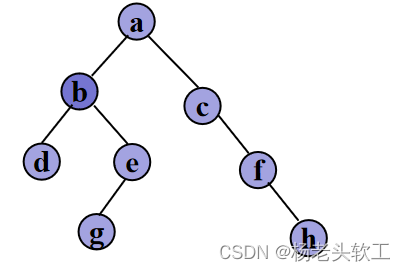
至此后序遍历该二叉树结束,遍历结果为:d g e b h f c a
5、重复访问标志
在此遍历过程中,会发现树根及子树的树根会被访问两次,为了避免这个问题,第一遇到的时候不访问,而第二次遇到的时候再访问,因此引入了一个访问标志。
三、后序遍历二叉树的源代码:
1、结点结构及条件编译
typedef struct node
{
datatype data;
struct node *Lchild;
struct node *Rchild;
int flag;
}BiTree;
#ifdef CHAR
typedef char datatype;
#else
typedef int datatype;
#endif
2、递归算法
void PostorderSearch_Recu( BiTree *T)
{
if (T!=NULL)
{
PostorderSearch_Recu(T->Lchild) ;
PostorderSearch_Recu(T->Rchild) ;
VisitNode(T->data) ;
}
}
3、非递归算法
void PostorderSearch( BiTree *T )
{
BiTree *p, *stack[ MAX_NODE ];
int top = 0;//栈顶位置下标
if( T == NULL )
{
return;
}
p = T;
while( 1 )
{
if( p != NULL )//p非空,则入栈,之后p向左走
{
stack[ top++ ] = p;
p = p->Lchild;
}
else//p为空,则出栈
{
p = stack[ --top ];
//右为空,且flag为真,则访问,之后p置空
if( p->Rchild == NULL || p->flag == 1 )
{
VisitNode( p->data );
p = NULL;
}
else//右非空,则p重新入栈,重复入栈标志flag置为真,之后p向右走
{
stack[ top++ ] = p;
p->flag = 1;
p = p->Rchild;
}
}
if( top == 0 )//栈为空,则结束遍历
{
break;
}
}
}
4、VisitNode函数如下:
void VisitNode( datatype data )
{
#ifdef CHAR
printf( "%5c", data );
#else
printf( "%5d", data );
#endif
}
补充:结合前面文章中的创建二叉树的算法,就可以完整的实现二叉树创建与后序遍历二叉树了。此处不再赘叙创建的算法。
边栏推荐
- FP5207电池升压 5V9V12V24V36V42V大功率方案
- Win11 system cannot find dll file how to fix
- 2021-10-14
- CMAKE
- win10怎么设置不睡眠熄屏?win10设置永不睡眠的方法
- Win10 cannot directly use photo viewer to open the picture
- Binder机制(下篇)
- Please make sure you have the correct access rights and the repository exists. Problem solved
- Win10 computer can't read U disk?Don't recognize U disk how to solve?
- 推开机电的大门《电路》(二):功率计算与判断
猜你喜欢
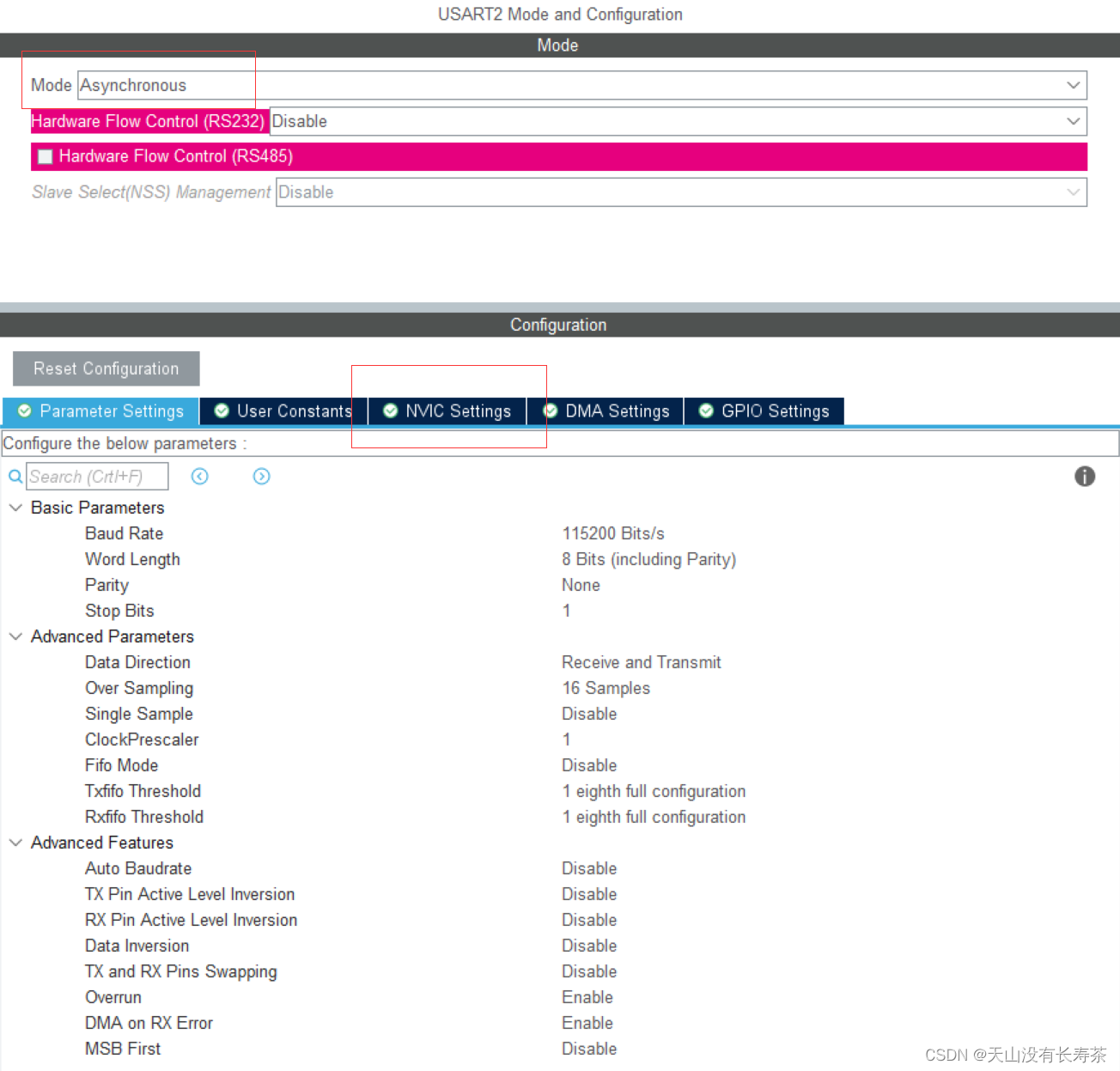
STM32LL库——USART中断接收不定长信息
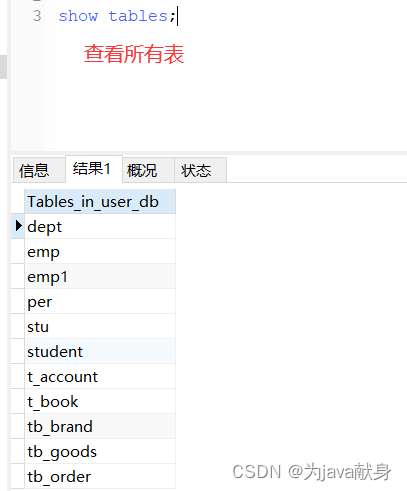
General syntax and usage instructions of SQL (picture and text)
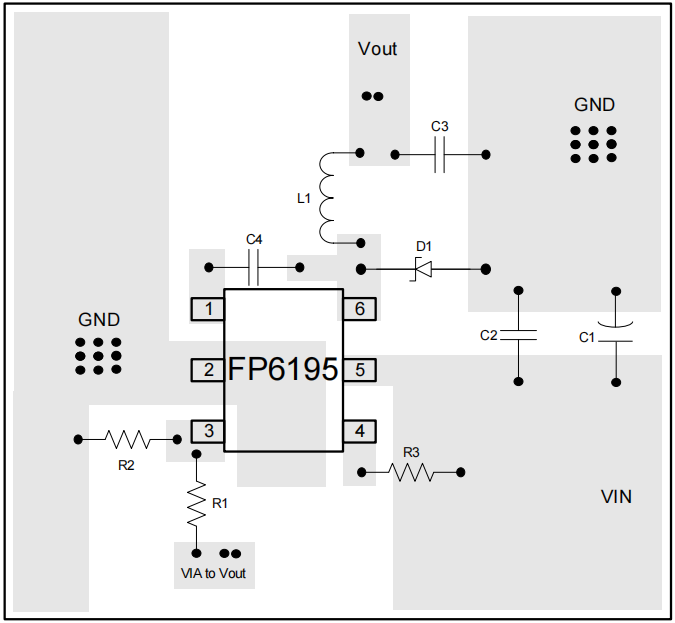
FP6195耐压60V电流降压3.3V5V模块供电方案
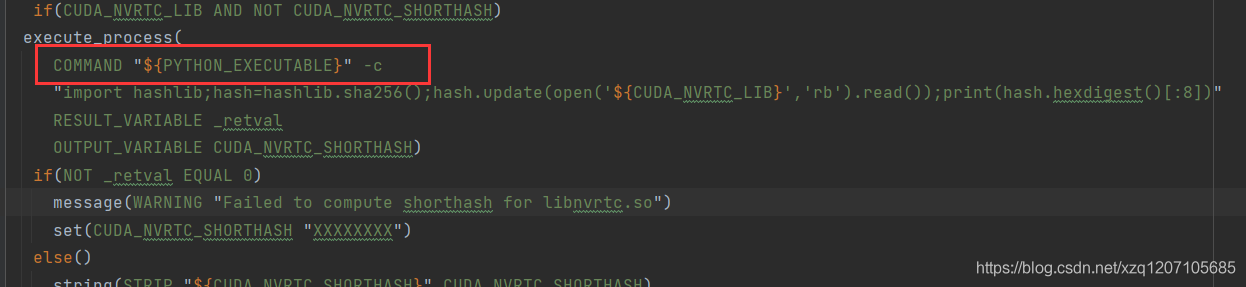
cmake配置libtorch报错Failed to compute shorthash for libnvrtc.so
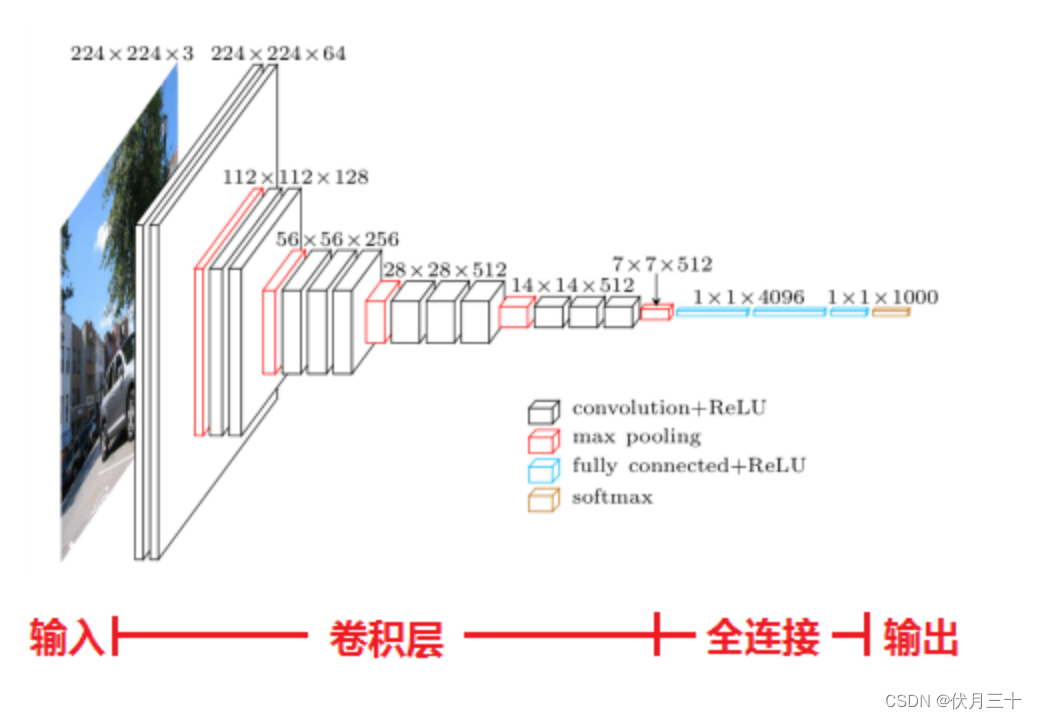
PyTorch⑨---卷积神经网络_线性层
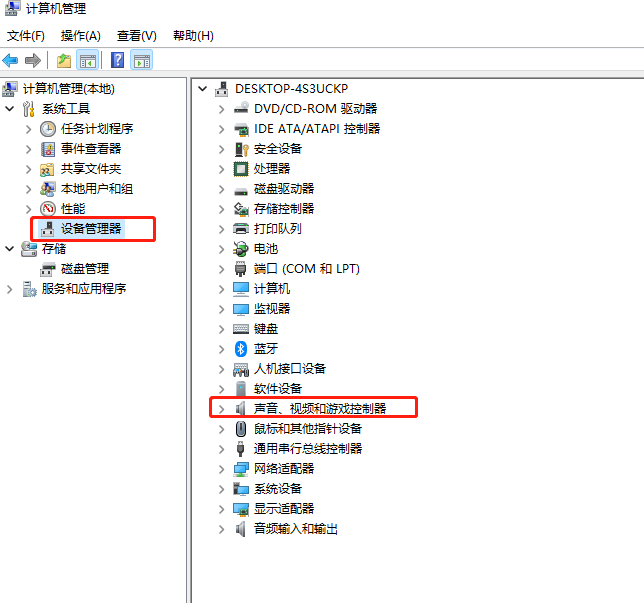
Win11声卡驱动如何更新?Win11声卡驱动更新方法
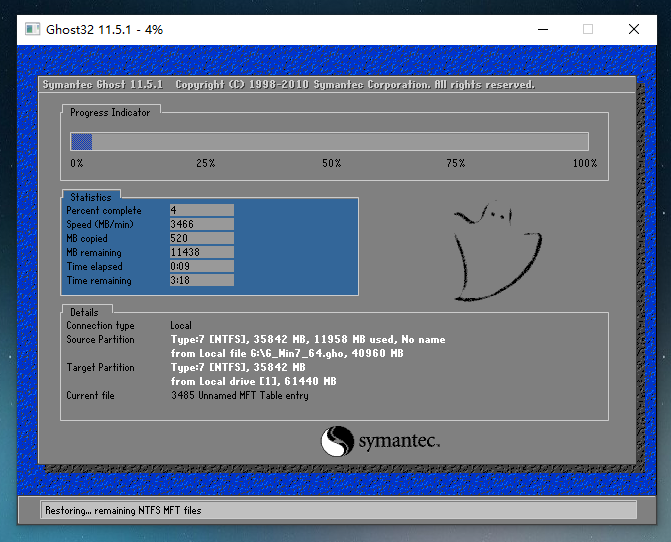
用U盘怎么重装Win7系统?如何使用u盘重装系统win7?
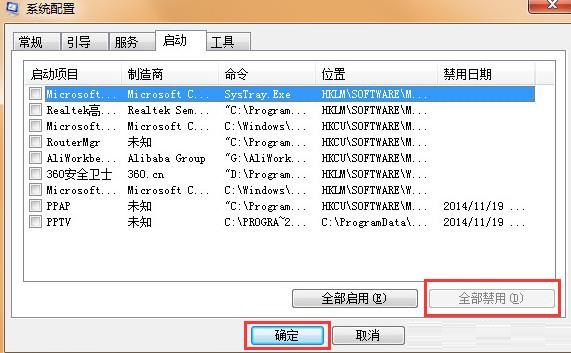
A clean start Windows 7?How to load only the basic service start Windows 7 system

How to solve Win11 without local users and groups
What is Win10 God Mode for?How to enable God Mode in Windows 10?
随机推荐
Win10无法连接打印机怎么办?不能使用打印机的解决方法
使用npx -p @storybook/cli sb init安装失败,手把手搭建专属的storybook
【我的电赛日记(完结)---2021全国大学生电子设计竞赛全国一等奖】A题:信号失真度测量装置
Bash shell位置参数
FP7195转模拟恒流调光芯片在机器视觉光源的应用优势
Win7怎么干净启动?如何只加载基本服务启动Win7系统
基于深度学习的配准框架
win10 system update error code 0x80244022 how to do
jest test, component test
PyTorch④---DataLoader的使用
Win10电脑不能读取U盘怎么办?不识别U盘怎么解决?
LeetCode2 电话号码的字母组合
5. Use RecyclerView to elegantly achieve waterfall effect
BLE蓝牙5.2-PHY6222系统级芯片(SoC)智能手表/手环
FP5207电池升压 5V9V12V24V36V42V大功率方案
用U盘怎么重装Win7系统?如何使用u盘重装系统win7?
2021-10-14
FP7195降压恒流PWM转模拟调光零压差大功率驱动方案原理图
编译error D8021 :无效的数值参数“/Wextra” cl command line error d8021 invalid numeric argument ‘/wextra‘
Win10 computer can't read U disk?Don't recognize U disk how to solve?