当前位置:网站首页>2022/8/4 树上差分+线段树
2022/8/4 树上差分+线段树
2022-08-04 22:48:00 【killer_queen4804】
活动地址:CSDN21天学习挑战赛
1416A - k-Amazing Numbers
要是暴力的话就太暴力了,但是我们可以把问题简化到只考虑坐标上,发现a的值域最大是n,所以可以直接枚举每个数,用vector存每个数的下标,用后一个下标值减去前一个,最后得出最大值就是这个数可以作为哪一个k-number,可以发现如果这个数可以作为k-num,那么k+1,k+2,,,n他都可以做,所以这也是为什么要从1到n开始枚举的原因,后面的如果也满足但是由于后面的数更大所以就直接break掉(因为这个还T了一次,,)就可以了,这样做会节省很多时间
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 2e5+5;
ll t,n,a[300005],vis[300005];
vector<ll>v[300005];
int main(){
scanf("%lld",&t);
while(t--){
scanf("%lld",&n);
for(int i=1;i<=n;i++) vis[i]=-1,v[i].clear();
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
v[a[i]].push_back(i);
}
for(int i=1;i<=n;i++){
if(v[i].size()==0) continue;
ll maxx=max(v[i][0]-0,n+1-v[i][v[i].size()-1]);
for(int j=1;j<v[i].size();j++){
maxx=max(maxx,v[i][j]-v[i][j-1]);
}
//cout<<maxx<<" "<<i<<endl;
if(maxx<=n){
while(maxx<=n){
if(vis[maxx]==-1) vis[maxx]=i;
else break;
maxx++;
}
}
}
for(int i=1;i<=n;i++) printf("%lld ",vis[i]);printf("\n");
}
system("pause");
return 0;
}
1374E1 - Reading Books (easy version)
本来还想用dp来着,但是一看范围就知道要寄了,其实想一下但是还是很好做的,设三个数组al里面放只有Alice喜欢的书,bo里面放只有bob喜欢的书,dou放两个人都喜欢的,这三个数组都是有序的,然后开始枚举就行了,如果dou里面的书比al和bo里面的书加起来花的时间少就选dou,否则就选al和bo;如果枚举的过程中al和bo至少有一个没有书了,那就只能依靠dou里面的书来去凑k,最后看看能不能凑成就行,因为是有序的所以答案一定是最小值
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 2e5+5;
ll n,k,al[200005],bo[200005],dou[200005];
struct node{
ll a,b,val;
bool operator<(const node& o)const{
return val<o.val;
}
}p[200005];
int main(){
scanf("%lld%lld",&n,&k);
ll ct1=0,ct2=0,ct3=0;
for(int i=1;i<=n;i++){
scanf("%lld%lld%lld",&p[i].val,&p[i].a,&p[i].b);
}
sort(p+1,p+n+1);
for(int i=1;i<=n;i++){
if(!p[i].a&&p[i].b) bo[++ct2]=p[i].val;
else if(p[i].a&&!p[i].b) al[++ct1]=p[i].val;
else if(p[i].a&&p[i].b) dou[++ct3]=p[i].val;
}
ll ali=0,bob=0,x=1,y=1,z=1,ans=0;
while(x<=ct1&&y<=ct2){
if(z<=ct3){
if(dou[z]<=al[x]+bo[y]){
ans+=dou[z];
z++;
ali++;bob++;
}
else{
ans+=al[x]+bo[y];
x++;y++;
ali++;bob++;
}
}
else{
ans+=al[x]+bo[y];
x++;y++;
ali++;bob++;
}
if(ali>=k&&bob>=k) break;
}
if(ali<k||bob<k){
while(z<=ct3){
ans+=dou[z];
z++;
ali++;bob++;
//cout<<ans<<" "<<z<<" "<<ali<<" "<<bob<<endl;
if(ali>=k&&bob>=k) break;
}
}
if(ali<k||bob<k) printf("-1\n");
else printf("%lld\n",ans);
system("pause");
return 0;
}
CF1076E Vasya and a Tree - 洛谷 | 树上差分
给u节点的d级子树加上x,那就在深度上做差分,mark[dep[u]]+=x;mark[dep[u]+d]-=x;之后还是直接向下遍历求和就可以,关键是回溯操作
【koko的算法课堂】最近公共祖先与树上差分_哔哩哔哩_bilibili
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 2e5+5;
ll n,m,mark[300005],sum,ans[300005];
ll head[600005],cnt;
struct Edge{
ll from,to,next;
}edge[600005];
void addedge(ll from,ll to){
edge[++cnt].from = from;
edge[cnt].to = to;
edge[cnt].next=head[from];
head[from]=cnt;
}
ll dep[300005];
vector<pair<ll,ll>>v[300005];
void dfs(ll u,ll fa){
dep[u]=dep[fa]+1;
// cout<<u<<" "<<fa<<endl;
for(int i=0;i<v[u].size();i++){
ll d=v[u][i].first+1,x=v[u][i].second;
mark[dep[u]]+=x;
// cout<<mark[dep[u]]<<" "<<d<<" "<<x<<endl;
if(dep[u]+d<=n) mark[dep[u]+d]-=x;
}
sum+=mark[dep[u]];ans[u]=sum;
for(int i=head[u];i;i=edge[i].next){
ll j=edge[i].to;
if(j!=fa) dfs(j,u);
}
sum-=mark[dep[u]];
for(int i=0;i<v[u].size();i++){
ll d=v[u][i].first+1,x=v[u][i].second;
mark[dep[u]]-=x;
if(dep[u]+d<=n) mark[dep[u]+d]+=x;
}
}
int main(){
scanf("%lld",&n);
for(int i=1;i<n;i++){
ll x,y;
scanf("%lld%lld",&x,&y);
addedge(x,y);addedge(y,x);
}
scanf("%lld",&m);
for(int i=1;i<=m;i++){
ll vv,d,x;
scanf("%lld%lld%lld",&vv,&d,&x);
v[vv].push_back({d,x});
}
dfs(1,0);
for(int i=1;i<=n;i++) printf("%lld ",ans[i]);
system("pause");
return 0;
}
P2824 [HEOI2016/TJOI2016]排序 - 洛谷 | 二分+线段树
线段树分裂合并的做法没有看懂,现在这里留个坑
可以转化成01排序,01区间排序的话就是区间修改,查询区间的1的个数就是区间查询,二分答案,每次把大于等于答案的数变为1,小于的数变为0,这样如果check返回的是1,那就说明在这个位置上的数要大于这次二分的mid,继续l=mid+1,否则r=mid-1,这个二分是满足单调性的
题解 P2824 【[HEOI2016]排序】 - 无晴 的博客 - 洛谷博客 (luogu.com.cn)
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 2e5+5;
ll n,m,q,a[200005];
struct qu{
ll op,l,r;
}ch[100005];
ll t[4*100005],lazy[4*200005];
void pushup(ll p){t[p]=t[p<<1]+t[p<<1|1];}
void build(ll l,ll r,ll p,ll x){
if(l==r){
t[p]=(a[l]>=x);
lazy[p]=0;
return;
}
ll mid=l+r>>1;
build(l,mid,p<<1,x);
build(mid+1,r,p<<1|1,x);
pushup(p);lazy[p]=0;
}
void pushdown(ll p,ll l,ll r){
if(!lazy[p]) return;
lazy[p<<1]=lazy[p<<1|1]=lazy[p];
if(lazy[p]==1){
ll mid=l+r>>1;
t[p<<1]=mid-l+1;t[p<<1|1]=r-mid;
}
else t[p<<1]=t[p<<1|1]=0;
lazy[p]=0;
}
void update(ll l,ll r,ll p,ll L,ll R,ll val){
if(L<=l&&r<=R){
t[p]=(r-l+1)*val;lazy[p]=(val?1:-1);
return;
}
if(L>r||l>R) return;
pushdown(p,l,r);
ll mid=l+r>>1;
update(l,mid,p<<1,L,R,val);
update(mid+1,r,p<<1|1,L,R,val);
pushup(p);
}
ll query(ll l,ll r,ll p,ll L,ll R){
if(L<=l&&r<=R) return t[p];
if(L>r||l>R) return 0;
pushdown(p,l,r);
ll mid=l+r>>1;
return query(l,mid,p<<1,L,R)+query(mid+1,r,p<<1|1,L,R);
}
ll querypoint(ll l,ll r,ll p,ll x){
if(l==x&&r==x) return t[p];
pushdown(p,l,r);
ll mid=l+r>>1;
if(x<=mid) return querypoint(l,mid,p<<1,x);
else return querypoint(mid+1,r,p<<1|1,x);
}
bool check(ll x){
build(1,n,1,x);
for(int i=1;i<=m;i++){
ll cnt1=query(1,n,1,ch[i].l,ch[i].r);
if(ch[i].op){
update(1,n,1,ch[i].l,ch[i].l+cnt1-1,1);
update(1,n,1,ch[i].l+cnt1,ch[i].r,0);
}
else{
update(1,n,1,ch[i].r-cnt1+1,ch[i].r,1);
update(1,n,1,ch[i].l,ch[i].r-cnt1,0);
}
}
return querypoint(1,n,1,q);
}
int main(){
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
for(int i=1;i<=m;i++) scanf("%lld%lld%lld",&ch[i].op,&ch[i].l,&ch[i].r);
scanf("%lld",&q);
ll l=1,r=n,ans=n+1;
while(l<=r){
ll mid=l+r>>1;
if(check(mid)) ans=mid,l=mid+1;
else r=mid-1;
}
printf("%lld\n",ans);
system("pause");
return 0;
}
边栏推荐
猜你喜欢
随机推荐
现在学习次世代3D游戏建模还能找到高薪好工作吗
1、网页结构
【无标题】
【字符串函数内功修炼】strcpy + strcat + strcmp(一)
文章占位 文章占位
torch单机多卡和多机多卡训练
后排乘客不系安全带?事故瞬间被甩出
【字符串函数内功修炼】strlen + strstr + strtok + strerror(三)
Service Mesh落地路径
Linux系统重启和停止Mysql服务教程
Autowired autowiring
限制tensorflow使用Cpu核数
被领导拒绝涨薪申请,跳槽后怒涨9.5K,这是我的心路历程
[Paper Notes KDD2021] MixGCF: An Improved Training Method for Graph Neural Network-based Recommender Systems
MySQL的JSON 数据类型1
To Offer | 03. Repeat Numbers in the array
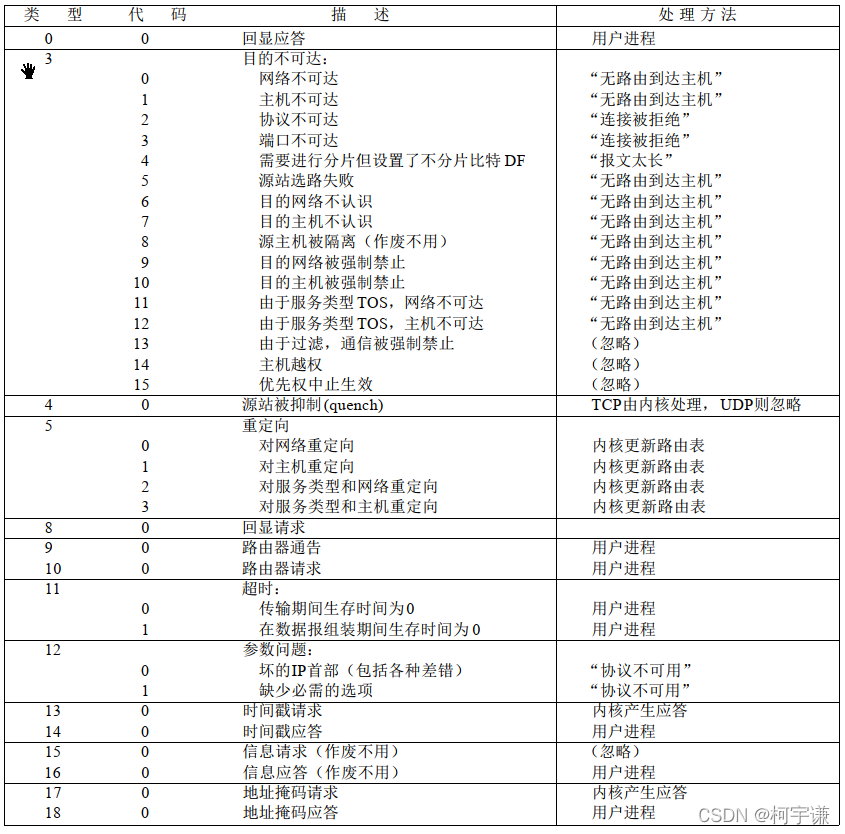
【TCP/IP 五 ICMP】
Numpy on the superposition of two arrays
论文解读(PPNP)《Predict then Propagate: Graph Neural Networks meet Personalized PageRank》
Operations on std::vector





![单片机原理[一] 学好单片机必会的五张图](/img/65/cac34bee5470ae85288d4366d8d957.jpg)
