【C】青蛙跳台阶和汉诺塔问题(递归)

博客主页:心辛向荣
系列专栏:【从0到1，C语言学习】
一句短话:你若盛开，蝴蝶自来！
博客说明:尽己所能，把每一篇博客写好，帮助自己熟悉所学知识，也希望自己的这些内容可以帮助到一些在学习路上的伙伴，文章中如果发现错误及不足之处，还望在评论区留言，我们一起交流进步！

前言

这篇博客总结递归当中俩个经典的问题，青蛙跳台阶和汉诺塔，用C语言实现！

一.青蛙跳台阶

题目：

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

解题思路：

n=1，跳一个台阶，只有一种跳法；

n = 2，先跳一个台阶，再跳一个台阶，或者直接跳俩个台阶，有俩种跳法；

n>2，青蛙跳第一次时，有俩种可能，即跳一个台阶或者跳俩个台阶，只需要将这俩种情况下的跳法加起来即可，用一个函数fib()实现求青蛙跳上一个 n 级的台阶总共有多少种跳法，那么结果为Fib(n - 1) + Fib(n - 2)。

用递归实现，

代码：

#include<stdio.h>
int Fib(int n)
{
    
	if (n <= 2)
	{
    
		return n;
	}
	if (n > 2)
	{
    
		return Fib(n - 1) + Fib(n - 2);
	}
}

int main()
{
    
	printf("输入台阶数n = ");
	int n = 0;
	scanf("%d", &n);

	printf("有%d种跳法\n", Fib(n));
	return 0;
}

运行结果：

二.汉诺塔

汉诺塔（Hanoi Tower），又称河内塔，源于印度一个古老传说。

大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照从大到小顺序摞着64片黄金圆盘。

大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。

并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。问应该如何操作？

题目：

这里我们实现这样一个过程，有A、B、C三个柱子，A柱上有n个盘子，将这n个盘子移动到C柱上，用代码实现移动过程并计算要进行多少次移动！

解题思路：

假如n=3，那么这三个盘子的移动过程如下：

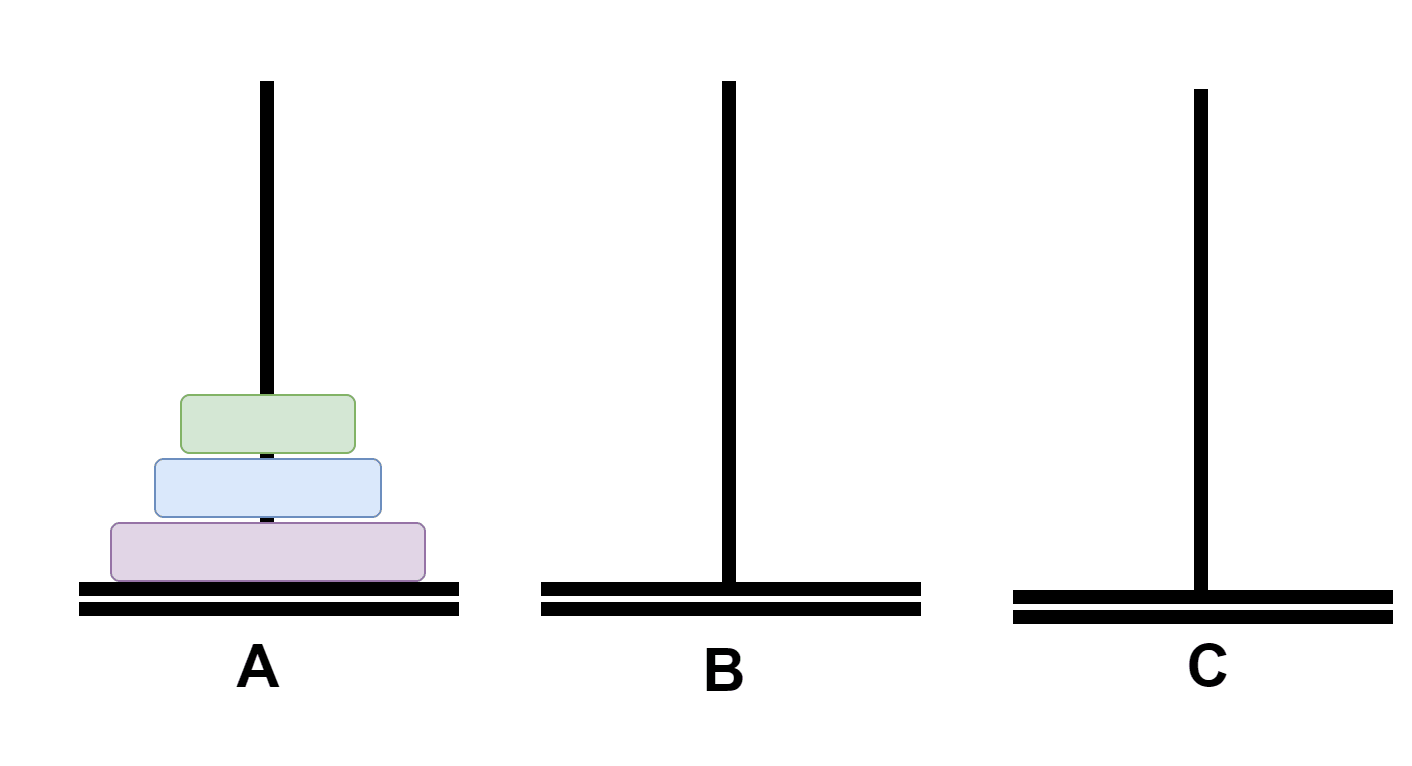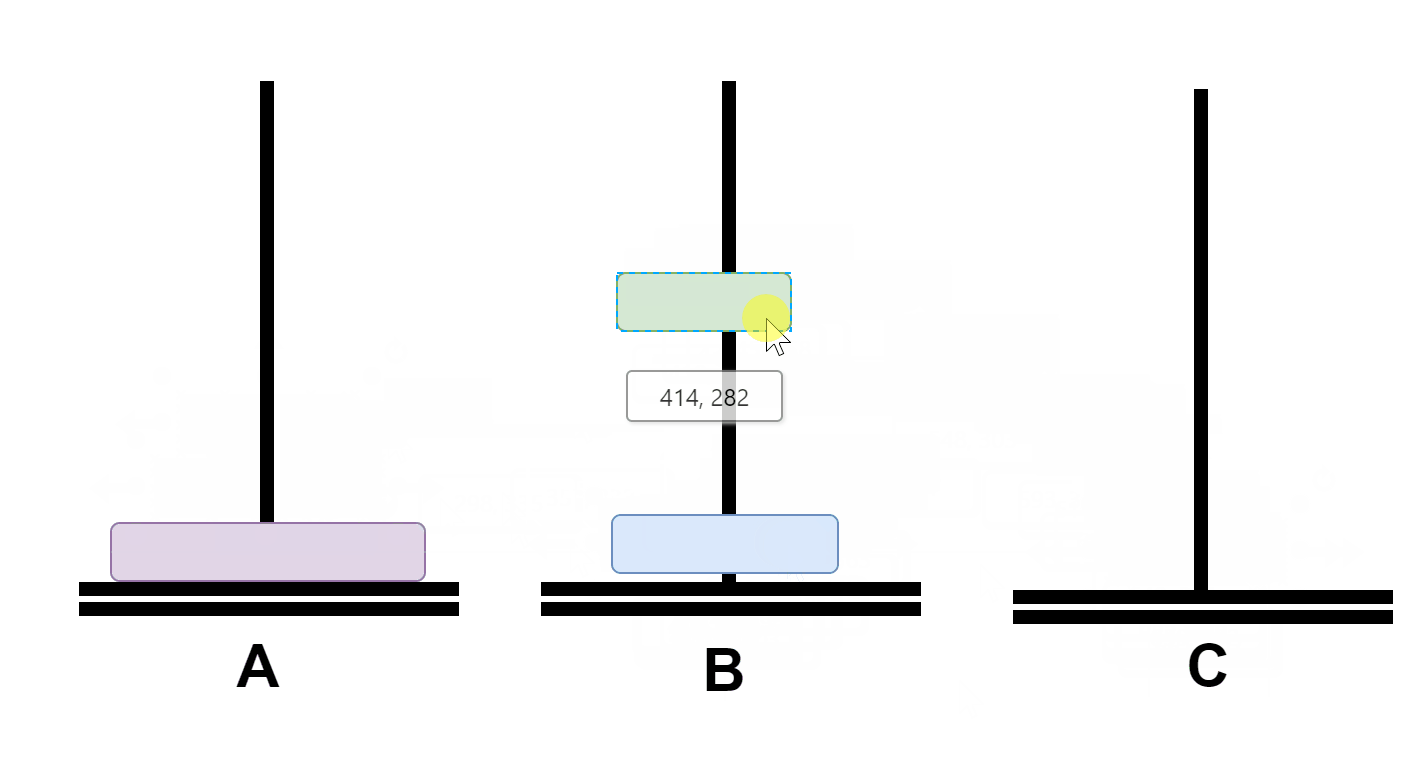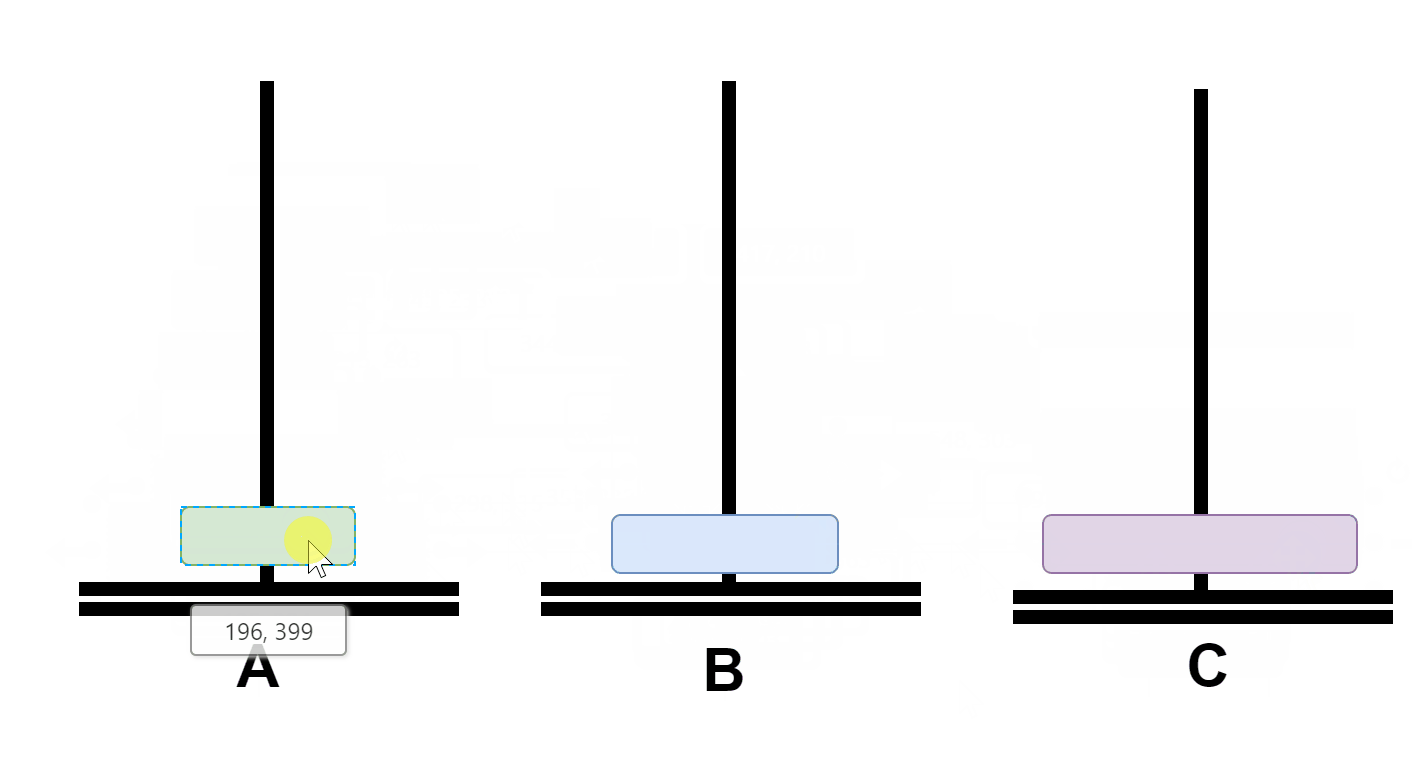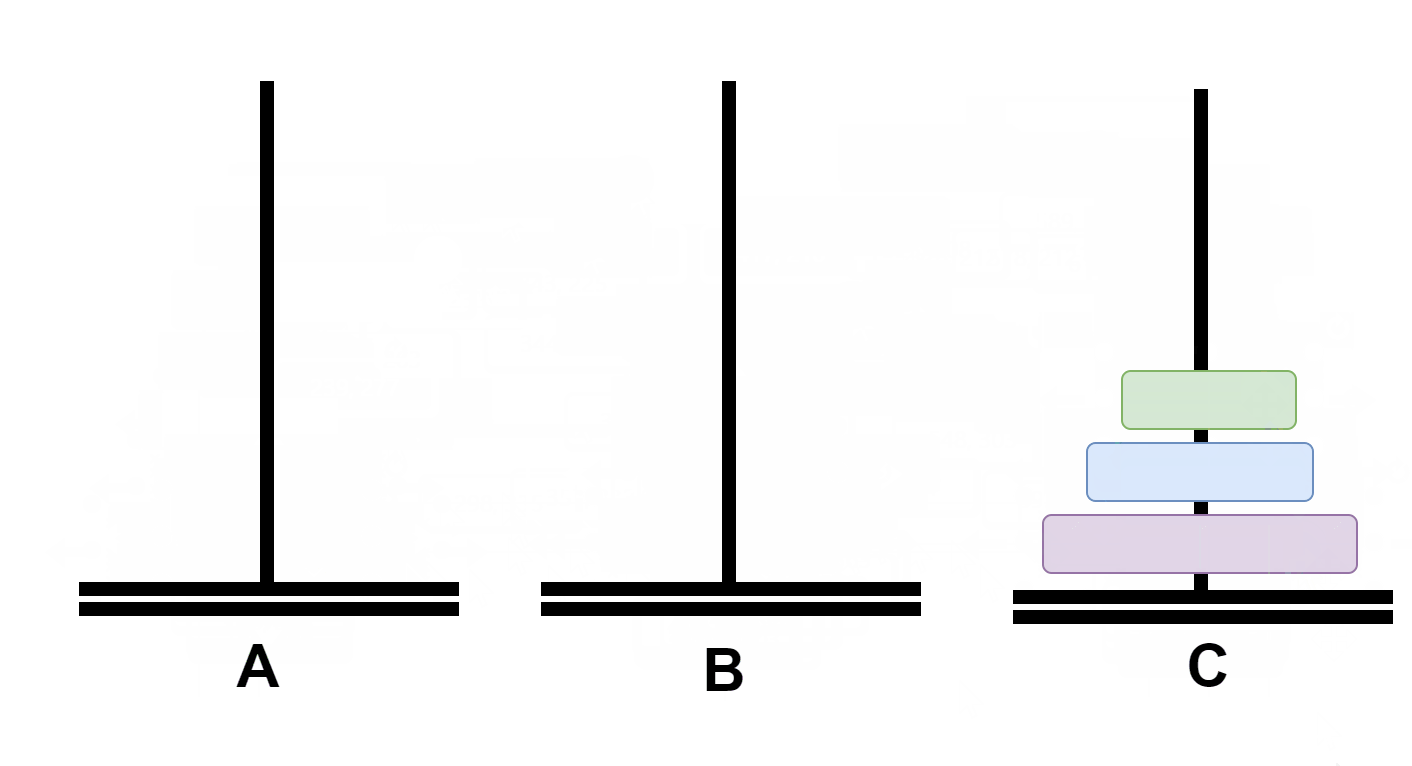
首先将A上面的俩个盘子通过C移动到B；

再将A上的盘子移动到C；

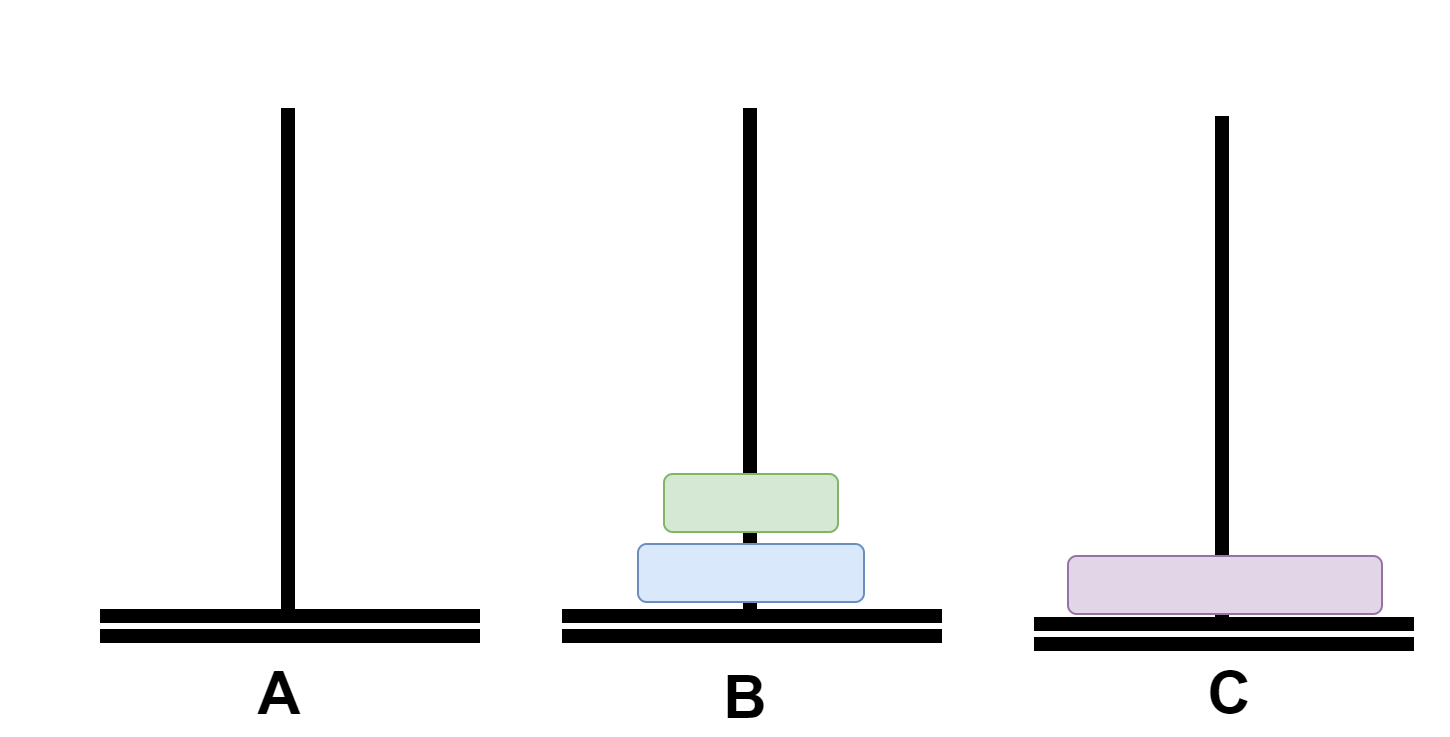
再将B上的俩个盘子通过A移动到C；

对于n个盘子，要将其通过B放到C上；

我们首先要实现A最下面的盘子放到C上，那么我们就先实现将A上面的n-1个盘子通过C放到B上，然后再将A上的最后一个盘子放到C上；

再将A上的盘子移动到C；

然后要实现将B上的盘子通过A放到C上，实现过程和上面类似，这个过程封装一个函数进行递归。

对于计算移动的次数，也可以用递归实现，思路如下：

当n = 1时，次数为1；

当n > 1时，

1. 计算将n-1个盘子从A通过B移动到C的次数
2. 将A上的最后一个盘子移动到C为一次
3. 将B上的盘子(n-1个)通过A移动到C

还可以按如下规律去求次数：

• 次数为2 ^ n - 1;

代码实现：

#include<stdio.h>
#include<math.h>

void Hannoi(int n, char A, char B, char C)
{
    
	if (1 == n)
	{
    
		printf("%c->%c ", A, C);
	}
	if (n > 1)
	{
    
		Hannoi(n - 1, A, C, B);
		printf("%c->%c ", A, C);
		Hannoi(n - 1, B, A, C);
	}

}

int Count_hannoi(int n)
{
    
	if (1 == n)
		return 1;
	if(n > 1)
	    return 2 * Count_hannoi(n - 1) + 1;
}

int main()
{
    
	printf("输入有几个盘子n = ");
	int n = 0;
	scanf("%d", &n);

	Hannoi(n, 'A', 'B', 'C');//打印移动过程

	/*printf("\n需要进行%d次移动\n", (int)pow(2,n) - 1);*/  //规律法
	printf("\n需要进行%d次移动\n", Count_hannoi(n));//递归法
	return 0;
}

运行结果：

结语

各位小伙伴，看到这里就是缘分嘛，希望我的这些内容可以给你带来那么一丝丝帮助，可以的话三连支持一下呗！！！ 感谢每一位走到这里的小伙伴，我们可以一起学习交流，一起进步！！！加油！！！