当前位置:网站首页>二叉搜索树(特性篇)
二叉搜索树(特性篇)
2022-07-07 14:17:00 【Joey Liao】
首先,BST 的特性大家应该都很熟悉了:
- 对于 BST 的每一个节点
node,左子树节点的值都比node的值要小,右子树节点的值都比node的值大。 - 对于 BST 的每一个节点 node,它的左侧子树和右侧子树都是 BST。
二叉搜索树并不算复杂,但我觉得它可以算是数据结构领域的半壁江山,直接基于 BST 的数据结构有 AVL 树,红黑树等等,拥有了自平衡性质,可以提供 logN 级别的增删查改效率;还有 B+ 树,线段树等结构都是基于 BST 的思想来设计的。
从做算法题的角度来看 BST,除了它的定义,还有一个重要的性质:BST 的中序遍历结果是有序的(升序)。
也就是说,如果输入一棵 BST,以下代码可以将 BST 中每个节点的值升序打印出来:
void traverse(TreeNode root) {
if (root == null) return;
traverse(root.left);
// 中序遍历代码位置
print(root.val);
traverse(root.right);
}
寻找第 K 小的元素
力扣第 230 题「 二叉搜索树中第 K 小的元素」
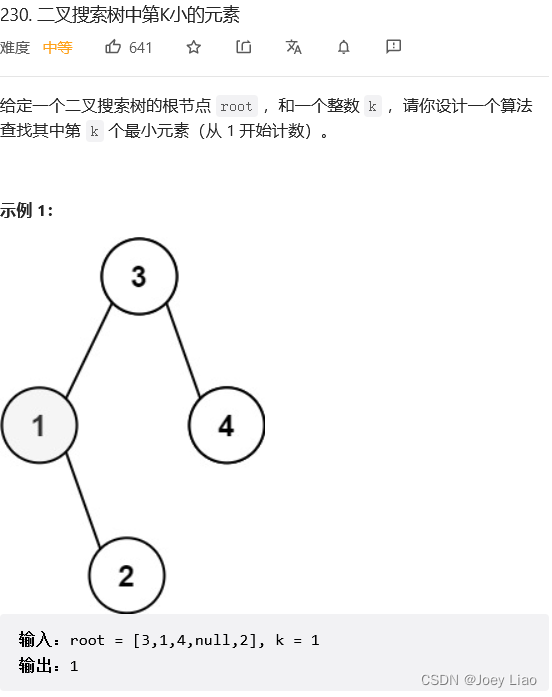
,一个直接的思路就是升序排序,然后找第 k 个元素呗。BST 的中序遍历其实就是升序排序的结果,找第 k 个元素肯定不是什么难事。
int kthSmallest(TreeNode root, int k) {
// 利用 BST 的中序遍历特性
traverse(root, k);
return res;
}
// 记录结果
int res = 0;
// 记录当前元素的排名
int rank = 0;
void traverse(TreeNode root, int k) {
if (root == null) {
return;
}
traverse(root.left, k);
/* 中序遍历代码位置 */
rank++;
if (k == rank) {
// 找到第 k 小的元素
res = root.val;
return;
}
/*****************/
traverse(root.right, k);
}
如果按照我们刚才说的方法,利用「BST 中序遍历就是升序排序结果」这个性质,每次寻找第 k 小的元素都要中序遍历一次,最坏的时间复杂度是 O(N),N 是 BST 的节点个数。
要知道 BST 性质是非常牛逼的,像红黑树这种改良的自平衡 BST,增删查改都是 O(logN) 的复杂度,让你算一个第 k 小元素,时间复杂度竟然要 O(N),有点低效了。
那么回到这个问题,想找到第 k 小的元素,或者说找到排名为 k 的元素,如果想达到对数级复杂度,关键也在于每个节点得知道他自己排第几。
比如说你让我查找排名为 k 的元素,当前节点知道自己排名第 m,那么我可以比较 m 和 k 的大小:
如果 m == k,显然就是找到了第 k 个元素,返回当前节点就行了。
如果 k < m,那说明排名第 k 的元素在左子树,所以可以去左子树搜索第 k 个元素。
如果 k > m,那说明排名第 k 的元素在右子树,所以可以去右子树搜索第 k - m - 1 个元素。
这样就可以将时间复杂度降到 O(logN) 了。
那么,如何让每一个节点知道自己的排名呢?
这就是我们之前说的,需要在二叉树节点中维护额外信息。每个节点需要记录,以自己为根的这棵二叉树有多少个节点。
也就是说,我们 TreeNode 中的字段应该如下:
class TreeNode {
int val;
// 以该节点为根的树的节点总数
int size;
TreeNode left;
TreeNode right;
}
有了 size 字段,外加 BST 节点左小右大的性质,对于每个节点 node 就可以通过 node.left 推导出 node 的排名,从而做到我们刚才说到的对数级算法。
当然,size 字段需要在增删元素的时候需要被正确维护,力扣提供的 TreeNode 是没有 size 这个字段的,所以我们这道题就只能利用 BST 中序遍历的特性实现了,但是我们上面说到的优化思路是 BST 的常见操作,还是有必要理解的。
BST 转化累加树
力扣第 538 题和 1038 题都是这道题 把二叉搜索树转换为累加树
其实就是二叉树的中序遍历,用sum来记录当前累加和
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */
class Solution {
int sum=0;
public TreeNode convertBST(TreeNode root) {
traverse(root);
return root;
}
public void traverse(TreeNode root){
if(root==null){
return ;
}
traverse(root.right);
sum+=root.val;
root.val=sum;
traverse(root.left);
}
}
边栏推荐
- Xcode Revoke certificate
- [Android -- data storage] use SQLite to store data
- 模仿企业微信会议室选择
- 企业级日志分析系统ELK
- asyncio 概念和用法
- AutoLISP series (3): function function 3
- laravel怎么获取到public路径
- 95.(cesium篇)cesium动态单体化-3D建筑物(楼栋)
- [hcsd celebrity live broadcast] teach the interview tips of big companies in person - brief notes
- 47_Opencv中的轮廓查找 cv::findContours()
猜你喜欢

Multiplication in pytorch: mul (), multiply (), matmul (), mm (), MV (), dot ()

Shandong old age Expo, 2022 China smart elderly care exhibition, smart elderly care and aging technology exhibition

Enterprise log analysis system elk

Eye of depth (VII) -- Elementary Transformation of matrix (attachment: explanation of some mathematical models)
![[C language] question set of X](/img/17/bfa57de183c44cf0a3c6637bb65a9d.jpg)
[C language] question set of X

Strengthen real-time data management, and the British software helps the security construction of the medical insurance platform
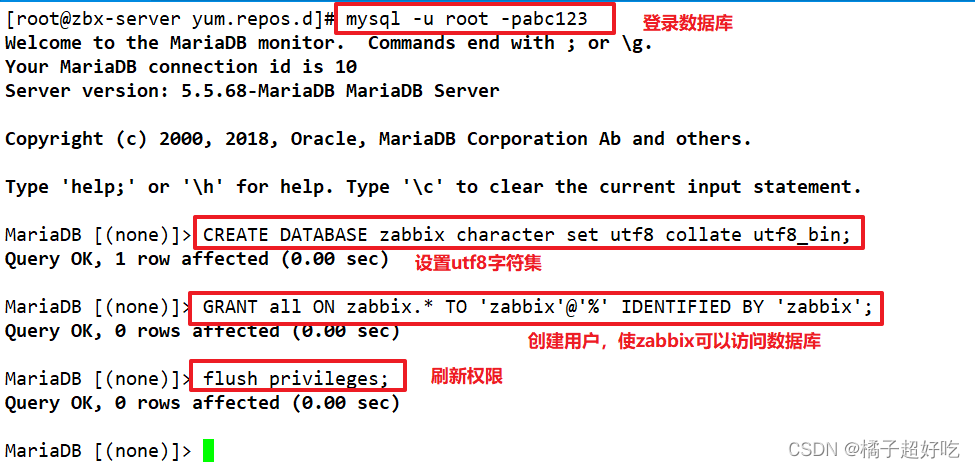
Plate - forme de surveillance par étapes zabbix
Mysql database basic operation DQL basic query
Statistical learning method -- perceptron

【Android -- 数据存储】使用 SQLite 存储数据
随机推荐
【知识小结】PHP使用svn笔记总结
95. (cesium chapter) cesium dynamic monomer-3d building (building)
Laravel service provider instance tutorial - create a service provider test instance
Notification uses full resolution
Statistical learning method -- perceptron
Logback日志框架第三方jar包 免费获取
统计学习方法——感知机
Laravel post shows an exception when submitting data
分步式監控平臺zabbix
Personal notes of graphics (1)
How to determine whether the checkbox in JS is selected
You Yuxi, coming!
[C language] question set of X
3000 words speak through HTTP cache
分类模型评价标准(performance measure)
js中复选框checkbox如何判定为被选中
Unity drawing plug-in = = [support the update of the original atlas]
Lecturer solicitation order | Apache seatunnel (cultivating) meetup sharing guests are in hot Recruitment!
Markdown formula editing tutorial
记录Servlet学习时的一次乱码