Merge multiple binary search trees

introduce

Here you are. n individual The root node of binary search tree , Stored in array trees in （ Subscript from 0 Start ）, Corresponding n A different binary search tree .trees Every binary search tree in At most 3 Nodes , And there are no two root nodes with the same value . In one step , The following steps will be completed ：

• Select two Different Subscript i and j , Requirements met in trees[i] One of the Leaf nodes The value is equal to the trees[j] Of Value of root node .
• use trees[j] Replace trees[i] The leaf node in .
• from trees Remove trees[j] .

If in execution n - 1 After the first operation , Can form an effective binary search tree , Returns the result of the binary tree The root node ; If we can't construct an effective binary search tree , return null .
Binary search tree is a kind of binary tree , And each node in the tree satisfies the following attributes ：

• The values in the left subtree of any node are Strictly less than The value of this node .
• The values in the right subtree of any node are Strictly greater than The value of this node .

Leaf nodes are nodes that do not contain child nodes .

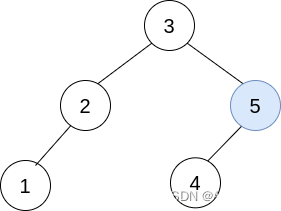
Example 1（ Success ）

Input ：trees = [[2,1],[3,2,5],[5,4]]
Output ：[3,2,5,1,null,4]
explain ：
In the first step , elect i=1 and j=0 , And will trees[0] Merge into trees[1] in .
Delete trees[0] ,trees = [[3,2,5,1],[5,4]] .

In the second step , elect i=0 and j=1 , take trees[1] Merge into trees[0] in .
Delete trees[1] ,trees = [[3,2,5,1,null,4]] .

The result tree is shown in the figure above , For an efficient binary search tree , So return to the root node of the tree .

Example 2（ Can't be ）

Input ：trees = [[5,3,8],[3,2,6]]
Output ：[]
explain ：
elect i=0 and j=1 , And then trees[1] Merge into trees[0] in .
Delete trees[1] ,trees = [[5,3,8,2,6]] .

The result tree is shown in the figure above . Only one valid operation can be performed , But the result tree is not an effective binary search tree , So back null .

Example 3

Input ：trees = [[5,4],[3]]
Output ：[]
explain ： Unable to perform any operation .

Tips

• n == trees.length
• 1 <= n <= 5 * 104
• The number of nodes in each tree is in the range [1, 3] Inside .
• Each node of input data may have child nodes, but there are no child nodes of child nodes
• trees There is no case in which the root node values of two trees are the same .
• All the trees in the input are Effective binary tree search tree .
• 1 <= TreeNode.val <= 5 * 104

For a given second $i$ tree $\text{tree}[i]$, Note that the value of its root node is $\text{root}[i]$. We need to find another tree , It's No $j(j\ne i)$ Tree . The first jj A tree must have a value of $\text{root}[i]$ Leaf node of , So we can put the $i$ A tree and the first $j$ Tree merging .

If there is no section that meets the requirements $j$ tree , So the first $i$ The root node of a tree must be the root node of the merged tree . obviously , Such a second $i$ A tree must have exactly one and only one .

If there is a unique $j$ tree , Then we have to put the $i$ A tree and $j$ Tree merging . If you don't do that , At least two values in the merged tree are $\text{root}[i]$ The node of , It must not be a binary search tree .

If there are multiple viable trees $j$ tree , So which tree should we choose ？ We found that , Because the title guarantees that there are no two root nodes with the same value , So, among the trees we didn't choose , Their values are $\text{root}[i]$ All leaf nodes will be preserved , And we chose the first $j$ A tree and the first $i$ When the trees merge , A value of $\text{root}[i]$ The node of . In this way, there are at least two values in the merged tree $\text{root}[i]$ The node of , It must not be a binary search tree .

therefore , If the root node of a tree needs to be merged , Then the merging scheme is the only one .

solution

• We first use a hash set of the values of each leaf node $\text{leaves}$ Store it , Then you can find the root node of the merged tree . Remember that the tree containing the root node is $\text{tree}[\text{pivot}]$, be $\text{root}[\text{pivot}]$ Can't be in $\text{leaves}$ There has been .（ The title says that there is no root node with the same value , So use hash Will be faster ）
  If there is no... That meets the requirements $\text{tree}[\text{pivot}]$, Then it is impossible to construct a binary search tree ; If the requirements are met $\text{tree}[\text{pivot}]$ Is not the only , Then we can choose one at random ( If the tree that meets the requirements is not unique, it is impossible to construct a binary search tree , This uniqueness is mentioned in the prompt ).

• We know , A binary tree is a binary search tree , If and only if its middle order ergodic sequence is strictly monotonically increasing . therefore , We from $\text{tree}[\text{pivot}]$ The root node of , Use the recursive method to perform a special middle order traversal ：

  • When we traverse to a non leaf node , We follow the conventional method of middle order traversal , Continue traversal ;
  • When we traverse to a leaf node , This leaf node may be merged with the root node of another tree . Let the value of this leaf node be xx, If there is a root node, the value is also xx The tree of , We will merge it with the leaf node . After the merger , The leaf node may become a non leaf node , We need to continue to follow the normal middle order traversal method , Continue traversal .

• In the process of traversal , If we find that the value traversed is not strictly monotonically increasing , Description cannot construct a binary search tree . meanwhile , If the traversal ends , However, the root node of a certain tree has not been traversed , That also means that we can't construct a binary search tree .

Code ：

/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */
class Solution {
    
public:
    TreeNode* canMerge(vector<TreeNode*>& trees) {
    
        //  A hash set that stores all leaf node values 
        unordered_set<int> leaves;
        //  Storage  ( Root node value ,  Trees )  Hash mapping of key value pairs 
        unordered_map<int, TreeNode*> candidates;
        for (TreeNode* tree: trees) {
    
            if (tree->left) {
    
                leaves.insert(tree->left->val);
            }
            if (tree->right) {
    
                leaves.insert(tree->right->val);
            }
            candidates[tree->val] = tree;
        }

        //  The stored sequence traverses the last traversed value , It is convenient to check the strict monotonicity 
        int prev = 0;
        
        //  In the sequence traversal , The return value indicates whether there is strict monotonicity 
        function<bool(TreeNode*)> dfs = [&](TreeNode* tree) {
    
            if (!tree) {
    
                return true;
            }

            //  If you traverse to the leaf node , And there are trees that can be merged , Then merge 
            if (!tree->left && !tree->right && candidates.count(tree->val)) {
    
                tree->left = candidates[tree->val]->left;
                tree->right = candidates[tree->val]->right;
                //  After the merger , Remove the tree from the hash map , In order to judge whether all trees have been traversed after traversal 
                candidates.erase(tree->val);
            }
            
            //  First traverse the left subtree 
            if (!dfs(tree->left)) {
    
                return false;
            }
            //  Then traverse the current node 
            if (tree->val <= prev) {
    
                return false;
            };
            prev = tree->val;
            //  Finally, traverse the right subtree 
            return dfs(tree->right);
        };
        
        for (TreeNode* tree: trees) {
    
            //  Find the root node of the merged tree 
            if (!leaves.count(tree->val)) {
    
                //  Remove it from the hash map 
                candidates.erase(tree->val);
                //  Start traversing from the root node 
                //  If the middle order ergodic is strictly monotonic , And the root nodes of all trees are traversed to , It shows that the binary search tree can be constructed 
                return (dfs(tree) && candidates.empty()) ? tree : nullptr;
            }
        }
        return nullptr;
    }
};