当前位置:网站首页>[combinatorics] combinatorial identities (sum of variable terms 3 combinatorial identities | sum of variable terms 4 combinatorial identities | binomial theorem + derivation to prove combinatorial ide
[combinatorics] combinatorial identities (sum of variable terms 3 combinatorial identities | sum of variable terms 4 combinatorial identities | binomial theorem + derivation to prove combinatorial ide
2022-07-03 15:57:00 【Programmer community】
List of articles
- One 、 Combinatorial identity ( Change the next term to sum ) Sum of variable coefficients 1
- Two 、 Combinatorial identity ( Change the next term to sum ) Sum of variable coefficients 1 prove ( binomial theorem + Derivation )
- 3、 ... and 、 Combinatorial identity ( Change the next term to sum ) Sum of variable coefficients 2
- Four 、 Combinatorial identity ( Change the next term to sum ) Sum of variable coefficients 2 prove ( Use known identities to prove )
One 、 Combinatorial identity ( Change the next term to sum ) Sum of variable coefficients 1
Combinatorial identity ( Change the next term to sum ) Sum of variable coefficients :
∑
k
=
0
n
k
(
n
k
)
=
n
2
n
−
1
\sum_{k=0}^{n} k \dbinom{n}{k} = n 2^{n-1}
k=0∑nk(kn)=n2n−1
k
k
k As the sum term changes , The range of change
0
0
0 ~
n
n
n ;
1. Method of proof :
- binomial theorem : Use binomial theorem + Derivation It can be proved that the combinatorial identity ;
- The combinatorial identity is substituted into : Use Known combinatorial identities are substituted into , Elimination coefficient ; That is, before using
3
3
3 Recursion , Simple and , Staggered and ,
5
5
5 Combinatorial identities Plug in ;
Two 、 Combinatorial identity ( Change the next term to sum ) Sum of variable coefficients 1 prove ( binomial theorem + Derivation )
Use binomial theorem + The derivation method proves the following identity :
∑
k
=
0
n
k
(
n
k
)
=
n
2
n
−
1
\sum_{k=0}^{n} k \dbinom{n}{k} = n 2^{n-1}
k=0∑nk(kn)=n2n−1
binomial theorem :
(
x
+
y
)
n
=
∑
k
=
0
n
(
n
k
)
x
k
y
n
−
k
(x + y)^n = \sum\limits_{k=0}^n \dbinom{n}{k}x^k y^{n-k}
(x+y)n=k=0∑n(kn)xkyn−k
1.
y
=
1
y = 1
y=1 Sometimes this happens :
(
x
+
1
)
n
=
∑
k
=
0
n
(
n
k
)
x
k
(x +1)^n = \sum\limits_{k=0}^n \dbinom{n}{k}x^k
(x+1)n=k=0∑n(kn)xk , In the above formula , Let the constant term
k
=
0
k= 0
k=0 The situation is calculated separately ,
(
n
0
)
x
0
=
1
\dbinom{n}{0}x^0 = 1
(0n)x0=1 , The calculation process is as follows :
(
x
+
1
)
n
=
∑
k
=
0
n
(
n
k
)
x
k
=
(
n
0
)
x
0
+
∑
k
=
1
n
(
n
k
)
x
k
=
1
+
∑
k
=
1
n
(
n
k
)
x
k
(x +1)^n = \sum\limits_{k=0}^n \dbinom{n}{k}x^k = \dbinom{n}{0}x^0 + \sum\limits_{k=1}^n \dbinom{n}{k}x^k = 1+ \sum\limits_{k=1}^n \dbinom{n}{k}x^k
(x+1)n=k=0∑n(kn)xk=(0n)x0+k=1∑n(kn)xk=1+k=1∑n(kn)xk
2. Introduce derivation : In addition to the summation
∑
k
=
1
n
(
n
k
)
x
k
\sum\limits_{k=1}^n \dbinom{n}{k}x^k
k=1∑n(kn)xk It appears that
k
k
k Number of changes , Need to be right
x
x
x To find the derivative ;
It's directly to
(
x
+
1
)
n
=
1
+
∑
k
=
1
n
(
n
k
)
x
k
(x +1)^n = 1+ \sum\limits_{k=1}^n \dbinom{n}{k}x^k
(x+1)n=1+k=1∑n(kn)xk Take derivatives on both sides of the equation ;
( 1 ) Left combined ( According to the following power function derivative formula Calculation ) :
(
x
+
1
)
n
(x +1)^n
(x+1)n Derivative is
n
(
x
+
1
)
n
−
1
n(x+1)^{n-1}
n(x+1)n−1
( 2 ) Right combination ( According to the following Derivative operation rules and Power function derivative formula Calculation ) :
1
+
∑
k
=
1
n
(
n
k
)
x
k
1+ \sum\limits_{k=1}^n \dbinom{n}{k}x^k
1+k=1∑n(kn)xk Derivative is ,
1
1
1 The derivative of by
0
0
0 , add
∑
k
=
1
n
(
n
k
)
x
k
\sum\limits_{k=1}^n \dbinom{n}{k}x^k
k=1∑n(kn)xk The derivative of
∑
k
=
1
n
k
(
n
k
)
x
k
−
1
\sum\limits_{k=1}^n k \dbinom{n}{k}x^{k-1}
k=1∑nk(kn)xk−1 , The end result is
∑
k
=
1
n
k
(
n
k
)
x
k
−
1
\sum\limits_{k=1}^n k \dbinom{n}{k}x^{k-1}
k=1∑nk(kn)xk−1
( 3 ) The left and right derivatives are equal :
n
(
x
+
1
)
n
−
1
=
∑
k
=
1
n
k
(
n
k
)
x
k
−
1
n(x+1)^{n-1} = \sum\limits_{k=1}^n k \dbinom{n}{k}x^{k-1}
n(x+1)n−1=k=1∑nk(kn)xk−1
Derivation of power function : ( Very important )
- Primitive function :
y
=
x
n
y = x^n
y=xn
- Corresponding derivative :
y
′
=
n
x
n
−
1
y' = nx^{n-1}
y′=nxn−1\
/
The derivative of a constant is0
0
0 ;
/
Four operations of derivative :(
u
±
v
)
′
=
u
′
±
v
′
(u \pm v)' = u' \pm v'
(u±v)′=u′±v′
/
Reference resources : derivative - Baidu Encyclopedia
3. The result of derivation is as follows :
n
(
x
+
1
)
n
−
1
=
∑
k
=
1
n
k
(
n
k
)
x
k
−
1
n(x+1)^{n-1} = \sum\limits_{k=1}^n k \dbinom{n}{k}x^{k-1}
n(x+1)n−1=k=1∑nk(kn)xk−1
Suppose... In the result of derivation
x
=
1
x = 1
x=1 , The results are as follows :
n
2
n
−
1
=
∑
k
=
1
n
k
(
n
k
)
n2^{n-1} = \sum\limits_{k=1}^n k \dbinom{n}{k}
n2n−1=k=1∑nk(kn)
When
k
=
0
k = 0
k=0 when , Yes
k
(
n
k
)
=
0
×
(
n
0
)
=
0
k \dbinom{n}{k} = 0 \times \dbinom{n}{0} = 0
k(kn)=0×(0n)=0 ,
So add
k
=
0
k=0
k=0 The situation of , namely
k
k
k from
0
0
0 Start accumulating , Nor does it affect the above results :
n
2
n
−
1
=
∑
k
=
0
n
k
(
n
k
)
n2^{n-1} = \sum\limits_{k=0}^n k \dbinom{n}{k}
n2n−1=k=0∑nk(kn)
3、 ... and 、 Combinatorial identity ( Change the next term to sum ) Sum of variable coefficients 2
Combinatorial identity ( Change the next term to sum ) Sum of variable coefficients :
∑
k
=
0
n
k
2
(
n
k
)
=
n
(
n
+
1
)
2
n
−
2
\sum_{k=0}^{n} k^2 \dbinom{n}{k} = n ( n+1 ) 2^{n-2}
k=0∑nk2(kn)=n(n+1)2n−2
k
k
k As the sum term changes , The range of change
0
0
0 ~
n
n
n ;
Method of proof :
- binomial theorem : Use binomial theorem + Derivation It can be proved that the combinatorial identity ;
- The combinatorial identity is substituted into : Use Known combinatorial identities are substituted into , Elimination coefficient ; That is, before using
3
3
3 Recursion , Simple and , Staggered and ,
5
5
5 Combinatorial identities Plug in ;
Four 、 Combinatorial identity ( Change the next term to sum ) Sum of variable coefficients 2 prove ( Use known identities to prove )
Use Known identities Prove the following identity :
∑
k
=
0
n
k
2
(
n
k
)
=
n
(
n
+
1
)
2
n
−
2
\sum\limits_{k=0}^{n} k^2 \dbinom{n}{k} = n ( n+1 ) 2^{n-2}
k=0∑nk2(kn)=n(n+1)2n−2
1. Enumeration of known identities :
- ① recursion
1
1
(
n
k
)
=
(
n
n
−
k
)
\dbinom{n}{k} = \dbinom{n}{n-k}
(kn)=(n−kn)
1 :
- ② recursion
2
2
(
n
k
)
=
n
k
(
n
−
1
k
−
1
)
\dbinom{n}{k} = \dfrac{n}{k} \dbinom{n - 1}{k - 1}
(kn)=kn(k−1n−1)
2 :
- ③ recursion
3
3
(
n
k
)
=
(
n
−
1
k
)
+
(
n
−
1
k
−
1
)
\dbinom{n}{k} = \dbinom{n - 1}{k} + \dbinom{n - 1}{k - 1}
(kn)=(kn−1)+(k−1n−1)
3 Pascal / Yang Hui's trigonometric formula :
- ④ Change the next term to sum 1 Simple and :
∑
k
=
0
n
(
n
k
)
=
2
n
\sum_{k=0}^{n}\dbinom{n}{k} = 2^n
k=0∑n(kn)=2n
- ⑤ Change the next term to sum 2 Staggered and :
∑
k
=
0
n
(
−
1
)
k
(
n
k
)
=
0
\sum_{k=0}^{n} (-1)^k \dbinom{n}{k} = 0
k=0∑n(−1)k(kn)=0
2. Variable lower limit : from
∑
k
=
0
n
k
2
(
n
k
)
\sum\limits_{k=0}^{n} k^2 \dbinom{n}{k}
k=0∑nk2(kn) Start deducing ,
k
=
0
k=0
k=0 when ,
k
2
(
n
k
)
=
0
k^2 \dbinom{n}{k} = 0
k2(kn)=0 , You can ignore , Here you can go from
1
1
1 Start accumulating ;
∑
k
=
0
n
k
2
(
n
k
)
=
∑
k
=
1
n
k
2
(
n
k
)
\sum\limits_{k=0}^{n} k^2 \dbinom{n}{k} = \sum\limits_{k=1}^{n} k^2 \dbinom{n}{k}
k=0∑nk2(kn)=k=1∑nk2(kn)
Use
(
n
k
)
=
n
k
(
n
−
1
k
−
1
)
\dbinom{n}{k} = \dfrac{n}{k} \dbinom{n - 1}{k - 1}
(kn)=kn(k−1n−1) Identity replaces one of
(
n
k
)
\dbinom{n}{k}
(kn) :
=
∑
k
=
1
n
k
2
n
k
(
n
−
1
k
−
1
)
= \sum\limits_{k=1}^{n} k^2 \dfrac{n}{k} \dbinom{n - 1}{k - 1}
=k=1∑nk2kn(k−1n−1)
3. Elimination coefficient : Eliminate one
k
k
k after , It becomes the following formula :
=
∑
k
=
1
n
k
n
(
n
−
1
k
−
1
)
=\sum\limits_{k=1}^{n} k n \dbinom{n - 1}{k - 1}
=k=1∑nkn(k−1n−1)
4. Constant mention : Among them
n
n
n Compared with summation , Is a constant , It can be mentioned beyond the summation symbol :
=
n
∑
k
=
1
n
k
(
n
−
1
k
−
1
)
=n\sum\limits_{k=1}^{n} k \dbinom{n - 1}{k - 1}
=nk=1∑nk(k−1n−1)
5. Deformation and disassembly : There are
(
n
−
1
k
−
1
)
\dbinom{n - 1}{k - 1}
(k−1n−1) , In order to
k
−
1
k-1
k−1 Match , There will be
k
k
k To deform ,
k
=
(
k
−
1
)
+
1
k = (k - 1) + 1
k=(k−1)+1 , Can come up with a
k
−
1
k-1
k−1 Come on ;
=
n
∑
k
=
1
n
[
(
k
−
1
)
+
1
]
(
n
−
1
k
−
1
)
=n\sum\limits_{k=1}^{n} [( k - 1 ) +1] \dbinom{n - 1}{k - 1}
=nk=1∑n[(k−1)+1](k−1n−1)
Using the summation formula , Disassemble the above formula into two sums ,
=
n
∑
k
=
1
n
(
k
−
1
)
(
n
−
1
k
−
1
)
+
n
∑
k
=
1
n
(
n
−
1
k
−
1
)
=n\sum\limits_{k=1}^{n} ( k - 1 ) \dbinom{n - 1}{k - 1} + n\sum\limits_{k=1}^{n} \dbinom{n - 1}{k - 1}
=nk=1∑n(k−1)(k−1n−1)+nk=1∑n(k−1n−1)
6. The first combinatorial transformation :
n
∑
k
=
1
n
(
k
−
1
)
(
n
−
1
k
−
1
)
n\sum\limits_{k=1}^{n} ( k - 1 ) \dbinom{n - 1}{k - 1}
nk=1∑n(k−1)(k−1n−1) Sum up ,
k
=
1
k=1
k=1 when , Next item of combinatorial number , The coefficient in the summation
k
−
1
=
0
k-1=0
k−1=0 , take
k
k
k Transform the lower bound ,
k
k
k The value is
1
1
1 ~
n
n
n , be
k
−
1
k-1
k−1 The value is
0
0
0 ~
(
n
−
1
)
(n-1)
(n−1) ,
It is equivalent to using
k
′
=
k
−
1
k' = k-1
k′=k−1 Replace the previous one
k
k
k ,
k
′
k'
k′ Value range
0
0
0 ~
(
n
−
1
)
(n-1)
(n−1) ,
So it can finally become
n
∑
k
′
=
0
n
−
1
(
k
′
)
(
n
−
1
k
′
)
n\sum\limits_{k'=0}^{n-1} ( k' ) \dbinom{n - 1}{k'}
nk′=0∑n−1(k′)(k′n−1)
Use
∑
k
=
0
n
k
(
n
k
)
=
n
2
n
−
1
\sum\limits_{k=0}^{n} k \dbinom{n}{k} = n 2^{n-1}
k=0∑nk(kn)=n2n−1 Combinatorial identity ,
Above
∑
k
′
=
0
n
−
1
(
k
′
)
(
n
−
1
k
′
)
\sum\limits_{k'=0}^{n-1} ( k' ) \dbinom{n - 1}{k'}
k′=0∑n−1(k′)(k′n−1) The result is
(
n
−
1
)
2
n
−
2
(n-1)2^{n-2}
(n−1)2n−2 ,
Front times
n
n
n , The final
n
∑
k
′
=
0
n
−
1
(
k
′
)
(
n
−
1
k
′
)
=
n
(
n
−
1
)
2
n
−
2
n\sum\limits_{k'=0}^{n-1} ( k' ) \dbinom{n - 1}{k'} = n(n-1)2^{n-2}
nk′=0∑n−1(k′)(k′n−1)=n(n−1)2n−2
7. The second combinatorial transformation :
n
∑
k
=
1
n
(
n
−
1
k
−
1
)
n\sum\limits_{k=1}^{n} \dbinom{n - 1}{k - 1}
nk=1∑n(k−1n−1) In this combination
k
k
k The value is
1
1
1 ~
n
n
n , take
k
k
k Change from
0
0
0 Start , That is to use
k
′
=
k
−
1
k' = k-1
k′=k−1 replace
k
k
k ,
Then there are
n
∑
k
′
=
0
n
−
1
(
n
−
1
k
′
)
n\sum\limits_{k'=0}^{n-1} \dbinom{n - 1}{k'}
nk′=0∑n−1(k′n−1) , This summation can be transformed into a basic summation ,
Use Simple and Combinatorial identity
∑
k
=
0
n
(
n
k
)
=
2
n
\sum\limits_{k=0}^{n}\dbinom{n}{k} = 2^n
k=0∑n(kn)=2n ,
∑
k
′
=
0
n
−
1
(
n
−
1
k
′
)
\sum\limits_{k'=0}^{n-1} \dbinom{n - 1}{k'}
k′=0∑n−1(k′n−1) Namely
2
n
−
1
2^{n-1}
2n−1 , Front times
n
n
n ,
n
∑
k
=
1
n
(
n
−
1
k
−
1
)
n\sum\limits_{k=1}^{n} \dbinom{n - 1}{k - 1}
nk=1∑n(k−1n−1) Namely
n
2
n
−
1
n2^{n-1}
n2n−1
=
n
∑
k
=
1
n
(
k
−
1
)
(
n
−
1
k
−
1
)
+
n
∑
k
=
1
n
(
n
−
1
k
−
1
)
=n\sum\limits_{k=1}^{n} ( k - 1 ) \dbinom{n - 1}{k - 1} + n\sum\limits_{k=1}^{n} \dbinom{n - 1}{k - 1}
=nk=1∑n(k−1)(k−1n−1)+nk=1∑n(k−1n−1)
=
n
(
n
−
1
)
2
n
−
2
+
n
2
n
−
1
=n(n-1)2^{n-2} + n2^{n-1}
=n(n−1)2n−2+n2n−1
=
n
(
n
−
1
)
2
n
−
2
+
n
2
×
2
n
−
2
=n(n-1)2^{n-2} + n 2 \times2^{n-2}
=n(n−1)2n−2+n2×2n−2
=
n
(
n
+
1
)
2
n
−
2
=n(n+1)2^{n-2}
=n(n+1)2n−2
summary :
First use of recursion , Eliminate the coefficient of variation
k
k
k ,
Add up each formula of the sum to the basic sum formula , or Known summation formula ,
Then sum and change the limit , That is to use
k
′
=
k
−
1
k' = k-1
k′=k−1 Replace
k
k
k ,
Through the above skills , Certificate of completion ;
边栏推荐
- 需要知道的字符串函数
- Low level version of drawing interface (explain each step in detail)
- Visual upper system design and development (Halcon WinForm) -4 Communication management
- Digital image processing -- popular understanding of corrosion and expansion
- CString在多线程中的问题
- UnityShader——MaterialCapture材质捕捉效果 (翡翠斧头)
- The difference between calling by value and simulating calling by reference
- 六月 致 -.-- -..- -
- The difference between mutually exclusive objects and critical areas
- Atlas atlas torque gun USB communication tutorial based on mtcom
猜你喜欢

String functions that you need to know

nifi从入门到实战(保姆级教程)——flow
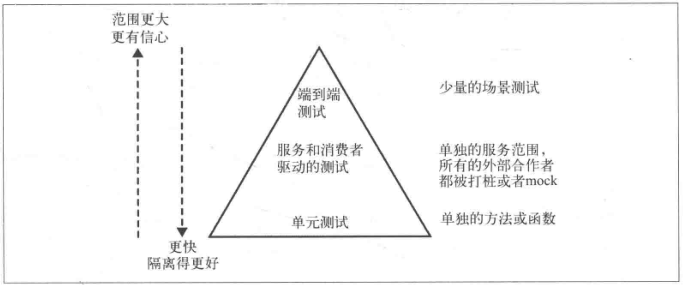
《微服务设计》读书笔记(下)

2022年Q2加密市场投融资报告:GameFi成为投资关键词

Project -- high concurrency memory pool

Popular understanding of linear regression (I)

请做好3年内随时失业的准备?

Unity function - unity offline document download and use
Srs4.0+obs studio+vlc3 (environment construction and basic use demonstration)

Distributed task scheduling XXL job
随机推荐
利用MySQL中的乐观锁和悲观锁实现分布式锁
CString中使用百分号
子类隐藏父类的同名函数
App mobile terminal test [5] file writing and reading
[系统安全] 四十三.Powershell恶意代码检测系列 (5)抽象语法树自动提取万字详解
Detailed explanation of string function and string function with unlimited length
Location of software installation information and system services in the registry
App移动端测试【5】文件的写入、读取
nifi从入门到实战(保姆级教程)——flow
Why can't strings be directly compared with equals; Why can't some integers be directly compared with the equal sign
Vs2017 is driven by IP debugging (dual machine debugging)
阿飞的期望
Unity function - unity offline document download and use
请求头不同国家和语言的表示
ASEMI整流桥UMB10F参数,UMB10F规格,UMB10F封装
How to thicken the brush in the graphical interface
“用Android复刻Apple产品UI”(2)——丝滑的AppStore卡片转场动画
坚持输出需要不断学习
半监督学习
秒杀系统3-商品列表和商品详情