当前位置:网站首页>Game Thinking 19: Multi-dimensional calculation related to games: point product, cross product, point-line-surface distance calculation
Game Thinking 19: Multi-dimensional calculation related to games: point product, cross product, point-line-surface distance calculation
2022-08-05 07:14:00 【Xie Baiyu】
文章目录
最近刷leecode遇到了这个问题,So by the way record
一、点乘
1)公式
对于向量a和向量b: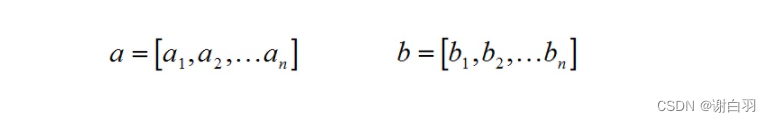
a和b的点积公式为:
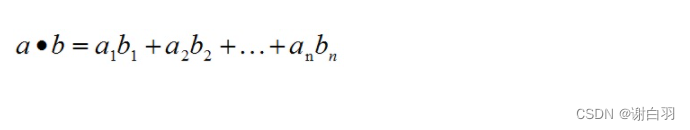
2)要求
A 1D vector is requireda和向量b的行列数相同.
3)几何意义
表征或计算两个向量之间的夹角,以及在b向量在a向量方向上的投影,有公式: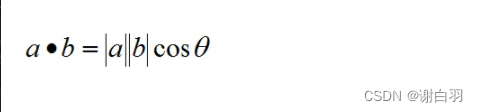
推导过程如下,首先看一下向量组成: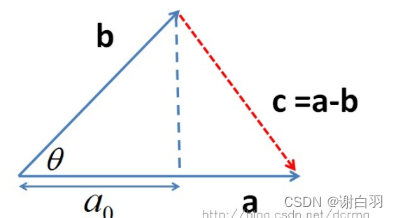
定义向量c:
According to the triangle cosine theorem:
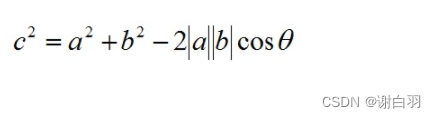
根据关系c=a-b(a、b、c均为向量)有:
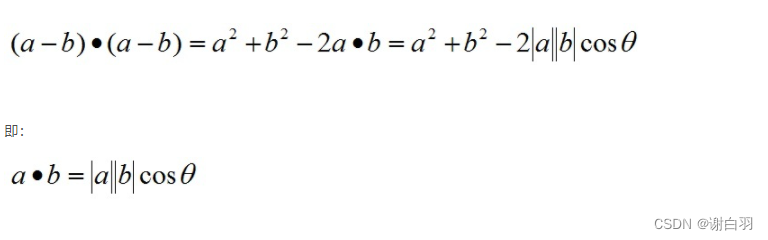
向量a,b的长度都是可以计算的已知量,从而有a和b间的夹角θ:
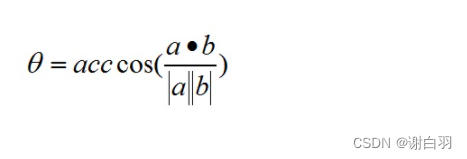
According to this formula, the vector can be calculateda和向量b之间的夹角.Thus, it can be further judged whether the two vectors are in the same direction,Is it orthogonal(也就是垂直)等方向关系,具体对应关系为:
1) a·b>0 方向基本相同,夹角在0°到90°之间
2)a·b=0 正交,相互垂直
3) a·b<0 方向基本相反,夹角在90°到180°之间
二、叉乘
1)叉乘公式
- 概念
两个向量的叉乘,又叫向量积、外积、叉积,叉乘的运算结果是一个向量而不是一个标量.并且两个向量的叉积与这两个向量组成的坐标平面垂直.
对于向量a和向量b:
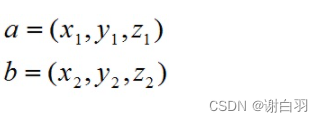
a和bThe formula for the cross product is :
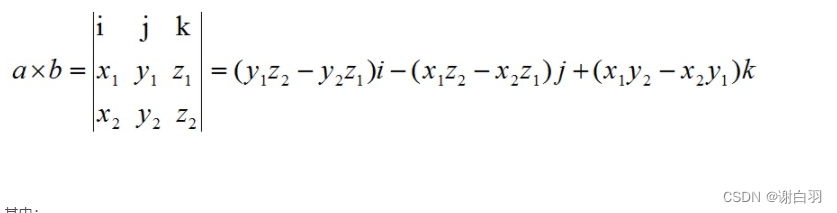
其中:
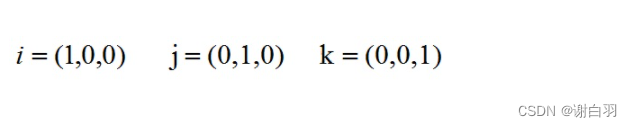
根据i、j、k间关系,有:
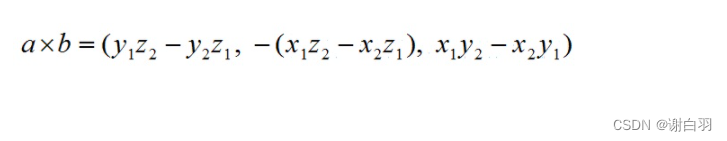
2)几何意义(1、构建法向量,2、计算平行四边形面积)
1)在三维几何中,向量a和向量b的叉乘结果是一个向量,更为熟知的叫法是法向量,该向量垂直于a和b向量构成的平面.
(在3D图像学中,叉乘的概念非常有用,可以通过两个向量的叉乘,生成第三个垂直于a,b的法向量,从而构建X、Y、Z坐标系.如下图所示: )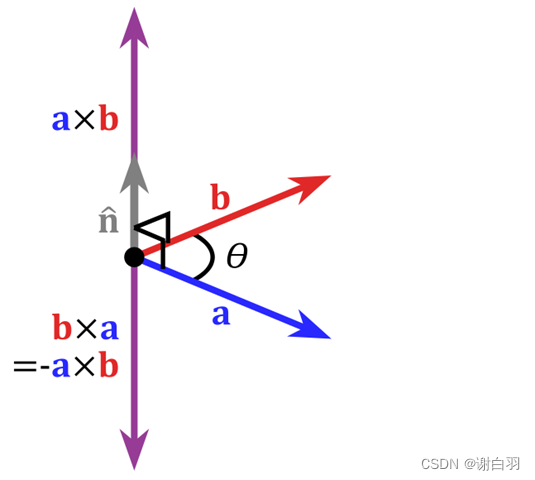
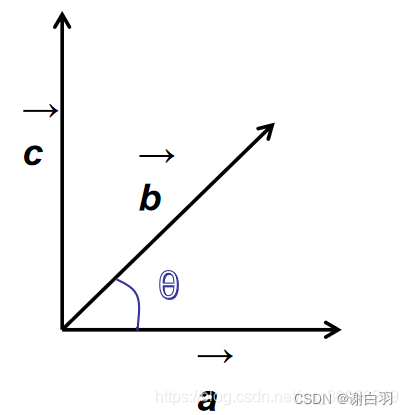
那么这个时候的a,b向量的叉乘结果
c=a×b=(a.x,a.y,a.z)×(b.x,b.y,b.z)=(a.y * b.z - a.z * b.y, a.z * b.x - a.x * b.z, a.x * b.y - a.y *
b.x)=(0,0,a.x * b.y - a.y * b.x)
即 c.z=a.x * b.y - a.y * b.x
The right-hand rule for the cross product of vectors determines the direction
如果k>0时,那么a正旋转到b的角度为<180°,
如果k<0,那么a正旋转到b的角度为>180°,
如果k=0 那么a,b向量平行.
1)a×b的方向:Four fingers bya开始,指向b,That's where the thumb pointsa×b的方向,垂直于a和b所在的平面
2)b×a的方向:Four fingers byb开始,指向a,That's where the thumb pointsb×a的方向,垂直于b和a所在的平面;
3)a×b的方向与b×a的方向是相反的,且有:a×b=-b×a.
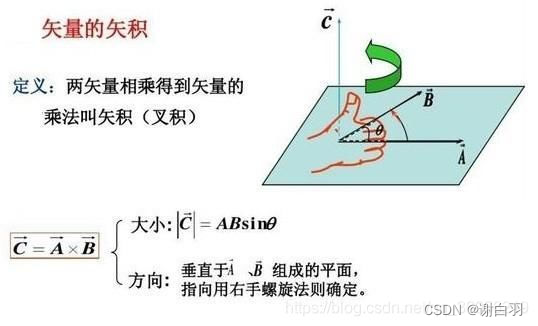
2)在二维空间中,叉乘还有另外一个几何意义就是:aXb等于由向量a和向量b构成的平行四边形的面积.
3)以leetcode题举例(这里没有z轴,故zThe calculated values for the axis coordinates are all 0)
- 469.凸多边形
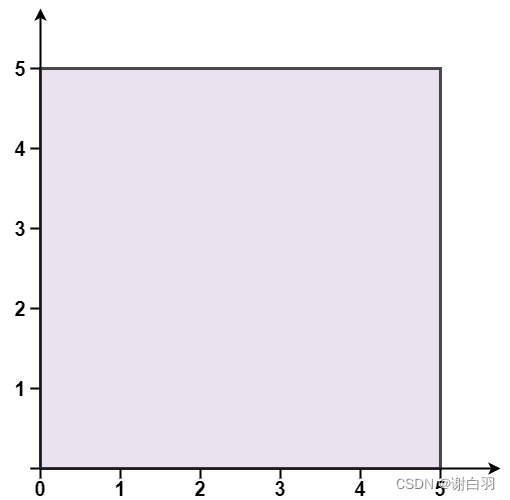
- 输入
输入: points = [[0,0],[0,5],[5,5],[5,0]]
输出: true
- 思路:
①设点0为A点,A点坐标(0,5);点B点为(0,5);点C为(5,0);点D为(0,0);
②算出AB、BC的法向量
int tmp = x1*y2 - x2*y1;
③算出BC和CD的法向量,与AB、BC的对比,小于0Explain that the normal vector is opposite,is not a convex polygon
if (tmp != 0)
{
if ((long long)pre * tmp < 0) //The direction of the previous normal vector is opposite
return false;
pre = tmp; //Save the last result
}
三、Calculate point, line and surface example problem
1)点到线段的最短距离
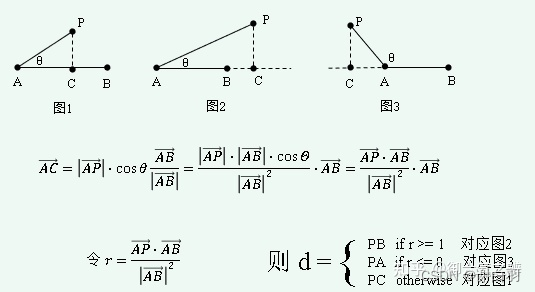

- 相关代码如下:
static float distancePtSeg2d(const float* pt, const float* p, const float* q)
{
float pqx = q[0] - p[0];
float pqz = q[2] - p[2];
float dx = pt[0] - p[0];
float dz = pt[2] - p[2];
float d = pqx*pqx + pqz*pqz;
float t = pqx*dx + pqz*dz;
if (d > 0)
t /= d;
if (t < 0)
t = 0;
else if (t > 1)
t = 1;
dx = p[0] + t*pqx - pt[0];
dz = p[2] + t*pqz - pt[2];
return dx*dx + dz*dz;
}
2)The shortest distance from a point to a polygon
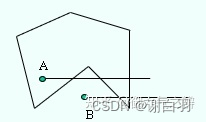
First calculate the distance from the point to all sides of the polygon,取最小值.如果点在多边形内,Take a negative number.You can use the ray method to determine whether a point is inside a polygon,If the ray intersects an odd number of sides of the polygon,means that the point is inside the polygon.
- 相关代码如下:
static float distToPoly(int nvert, const float* verts, const float* p)
{
float dmin = FLT_MAX;
int i, j, c = 0;
for (i = 0, j = nvert-1; i < nvert; j = i++)
{
const float* vi = &verts[i*3];
const float* vj = &verts[j*3];
if (((vi[2] > p[2]) != (vj[2] > p[2])) &&
(p[0] < (vj[0]-vi[0]) * (p[2]-vi[2]) / (vj[2]-vi[2]) + vi[0]) )
c = !c;
dmin = rcMin(dmin, distancePtSeg2d(p, vj, vi));
}
return c ? -dmin : dmin;
}
3)The distance from the point to the triangle face
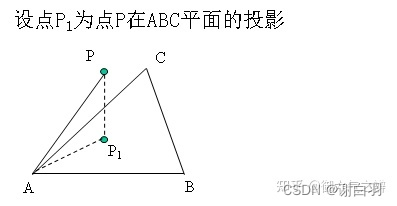

when the projection pointP1when outside the triangle,distanceFLT_MAX;when the projection pointP1when inside the triangle,The distance is in pointsP与点P1的yThe absolute value of the difference between the coordinates.投影点P1The conditions that need to be satisfied in the triangle are :

- 相关代码如下:
static float distPtTri(const float* p, const float* a, const float* b, const float* c)
{
float v0[3], v1[3], v2[3];
rcVsub(v0, c,a);
rcVsub(v1, b,a);
rcVsub(v2, p,a);
const float dot00 = vdot2(v0, v0);
const float dot01 = vdot2(v0, v1);
const float dot02 = vdot2(v0, v2);
const float dot11 = vdot2(v1, v1);
const float dot12 = vdot2(v1, v2);
// Compute barycentric coordinates
const float invDenom = 1.0f / (dot00 * dot11 - dot01 * dot01);
const float u = (dot11 * dot02 - dot01 * dot12) * invDenom;
float v = (dot00 * dot12 - dot01 * dot02) * invDenom;
// If point lies inside the triangle, return interpolated y-coord.
static const float EPS = 1e-4f;
if (u >= -EPS && v >= -EPS && (u+v) <= 1+EPS)
{
const float y = a[1] + v0[1]*u + v1[1]*v;
return fabsf(y-p[1]);
}
return FLT_MAX;
}
边栏推荐
猜你喜欢
随机推荐
[Shanghai] Hiring .Net Senior Software Engineer & BI Data Warehouse Engineer (Urgent)
Flink Learning 11: Flink Program Parallelism
Does Libpq support read-write separation configuration?
UDP broadcast
Re regular expressions
环网冗余式CAN/光纤转换器 CAN总线转光纤转换器中继集线器hub光端机
C# FileSystemWatcher
TCP的粘包拆包问题+解决方案
2022 Fusion Welding and Thermal Cutting Operation Certificate Exam Questions and Mock Exams
线程池的使用(结合Future/Callable使用)
对数据类型而言运算符无效。运算符为 add,类型为 text。
蓝牙gap协议
AI+视频技术助力保障校园安全,校园智能安防平台该如何建设?
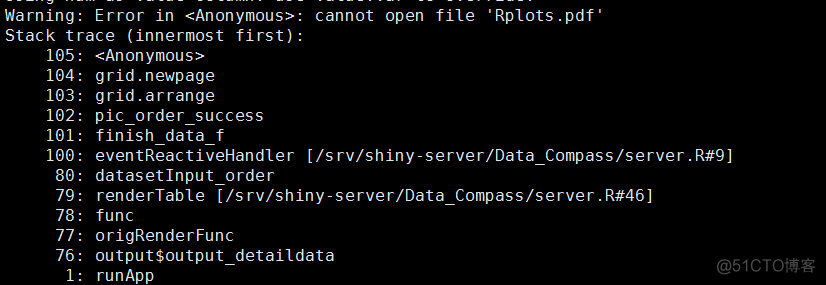
RNote108---Display the running progress of the R program
MySQL: order by sorting query, group by grouping query
2022.8.2 模拟赛
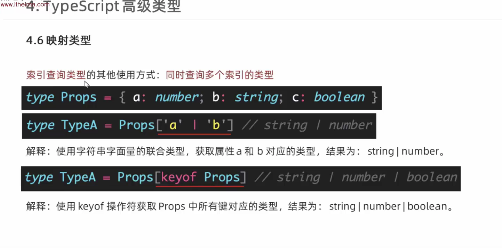
typescript68-索引查询类型(查询多个)
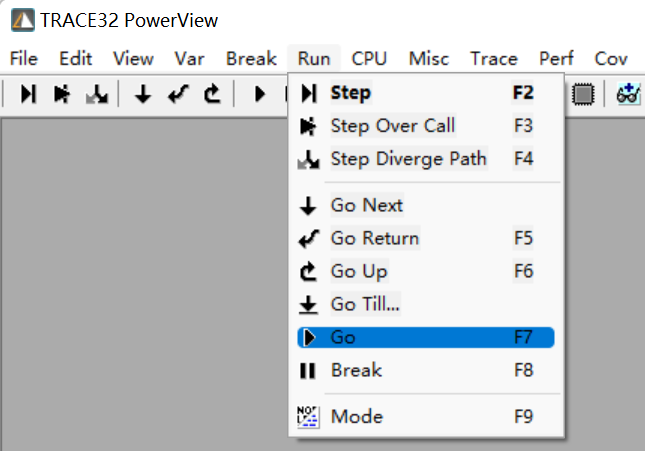
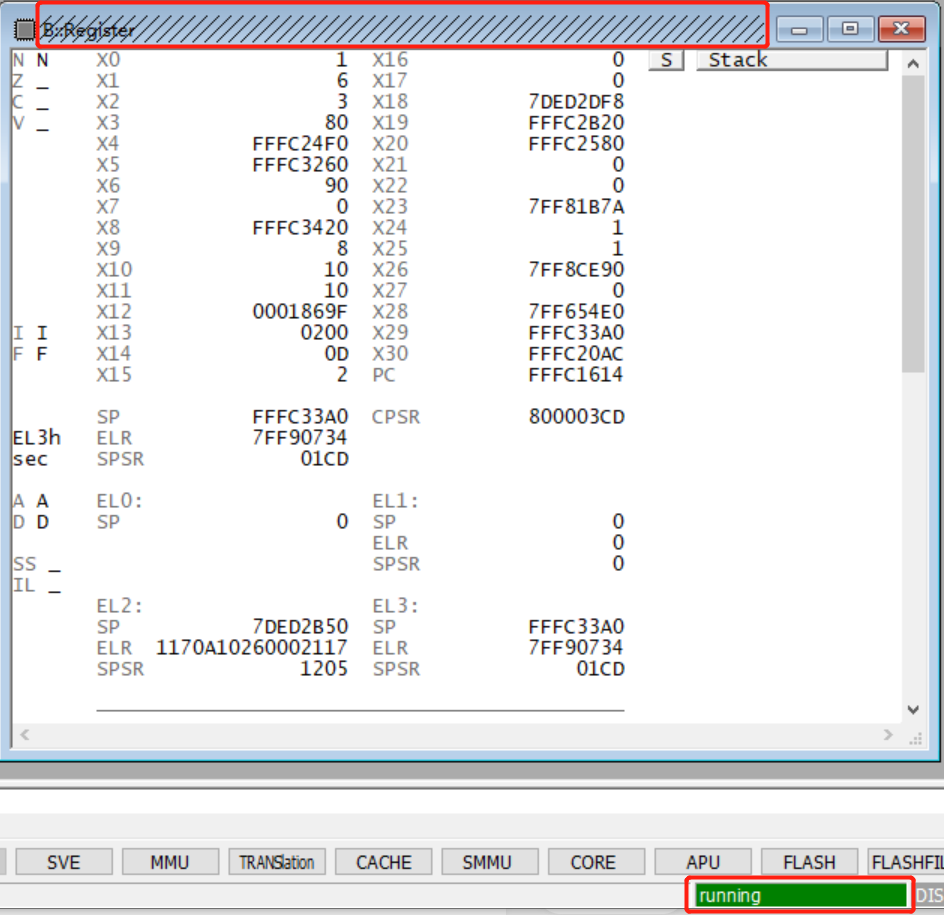
TRACE32——外设寄存器查看与修改
真实字节跳动测试开发面试题,拿下年薪50万offer。
风控特征的优化分箱,看看这样教科书的操作