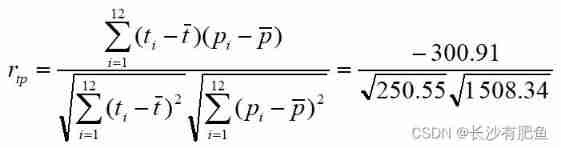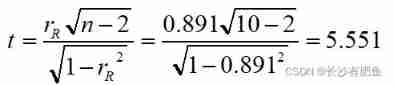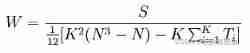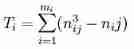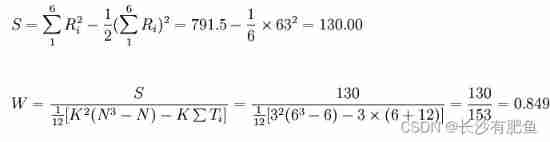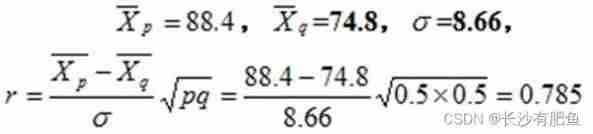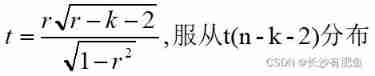当前位置:网站首页>Correlation analysis summary
Correlation analysis summary
2022-07-03 23:40:00 【Changsha has fat fish】
Correlation analysis
Correlation analysis :
- Measure the linear correlation between things or variables , And the process expressed by appropriate statistical indicators .
- such as , Household income and expenditure 、 A person's education level is related to his income 、 Children's height and parents' height, etc
The correlation coefficient :
- A measure of the degree of correlation between variables
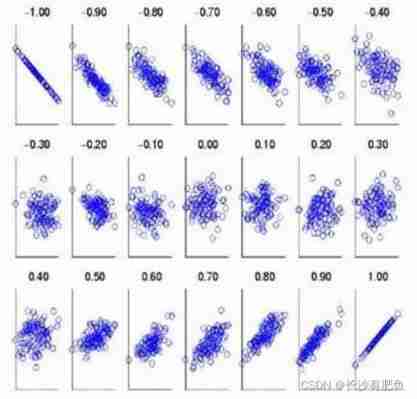
- The correlation coefficient r The value range of is one 1 To ten 1 Between
- The correlation coefficient r The sign of indicates the direction of change .“+” The sign indicates that the change direction is the same , That is, positive correlation ;“-” The sign indicates that the direction of change is opposite , Negative correlation
- r The absolute value of indicates the closeness between variables ( Strength ). The closer the absolute value is 1, Indicates that the closer the relationship between two variables ; The closer the 0, Indicates that the less closely the relationship between two variables
- The value of the correlation coefficient , Just a ratio . It is not measured in equal units ( That is, unequal distance ), It's not a percentage , therefore , You can't add directly 、 reduce 、 ride 、 In addition to the operation
- The correlation coefficient can only describe the change direction and closeness between two variables , It can not reveal the internal essential relationship between the two , That is, there are two related variables , There is not necessarily a causal relationship
Correlation analysis of continuous variables
Continuous variables are data variables , Its values can be compared , The difference can be calculated by addition and subtraction . Such as “ Age ”、“ income ”、“ achievement ” Equivariant .
When both variables are normal continuous variables , And when there is a linear relationship between the two , Usually use Pearson Correlation coefficient to measure
Pearson The correlation coefficient
covariance :
Covariance is an indicator of the correlation between two random variables , If one variable becomes larger or smaller at the same time as another variable , Then the covariance of these two variables is positive
Although covariance can reflect the degree of correlation between two random variables ( Covariance greater than 0 The two are positively correlated , Less than 0 It means that there is a negative correlation between the two ), However, the size of the covariate difference can not well measure the correlation degree of two random variables .
Some data are distributed in two-dimensional space , We want to know the coordinates of data points X Axis and Y The degree of relevance of the axis , If X And Y The degree of correlation is small, but the data distribution is relatively discrete , This will lead to a large difference in the calculated covariance , It is unreasonable to use this value to measure the degree of correlation
******pearson It's a gap between -1 and 1 Between the value of the , When the linear relationship between two variables increases , The correlation coefficient tends to 1 or -1; When a variable increases , When another variable also increases , It shows that there is a positive correlation between them , The correlation coefficient is greater than 0; If a variable increases , The other variable decreases , It shows that there is a negative correlation between them , The correlation coefficient is less than 0; If the correlation coefficient is equal to 0, It shows that there is no linear correlation between them .*******
-------(np.corrcoef(a) The correlation coefficient between rows can be calculated ,np.corrcoef(a,rowvar=0) Used to calculate the correlation coefficient between columns )-------
import numpy as np a = np.array([[10, 10, 8, 9, 7], [4, 5, 4, 3, 3], [3, 3, 1, 1, 1]]) aarray([[10, 10, 8, 9, 7], [ 4, 5, 4, 3, 3], [ 3, 3, 1, 1, 1]])np.corrcoef(a)#3*3array([[1. , 0.64168895, 0.84016805], [0.64168895, 1. , 0.76376262], [0.84016805, 0.76376262, 1. ]])np.corrcoef(a,rowvar=0) #5*5array([[1. , 0.98898224, 0.9526832 , 0.9939441 , 0.97986371], [0.98898224, 1. , 0.98718399, 0.99926008, 0.99862543], [0.9526832 , 0.98718399, 1. , 0.98031562, 0.99419163], [0.9939441 , 0.99926008, 0.98031562, 1. , 0.99587059], [0.97986371, 0.99862543, 0.99419163, 0.99587059, 1. ]])example :
The monthly average temperature and precipitation in London
Calculate the monthly average temperature in London (t) And precipitation (p) The correlation coefficient between
The results show that , The monthly average temperature in London (t) And precipitation (p) There is a negative correlation between them , That is, heterotropic Correlation
Significance test of correlation coefficient
hypothesis
- H0: ρ=0
- H1: ρ≠0
statistic
example: 10 The correlation coefficient between the math scores of students in grade one and grade two is 0.87, On the whole , Whether there is a correlation between the math scores of grade one and grade two ?
Calculate the test statistics :
therefore , On the whole , There is a positive correlation between the first grade math score and the second grade math score .
API file :
Statistical functions (scipy.stats) — SciPy v0.19.1 Reference Guide
python example :
import numpy as np import scipy.stats as stats import scipy x = [10.35, 6.24, 3.18, 8.46, 3.21, 7.65, 4.32, 8.66, 9.12, 10.31] y = [5.1, 3.15, 1.67, 4.33, 1.76, 4.11, 2.11, 4.88, 4.99, 5.12] correlation,pvalue = stats.stats.pearsonr(x,y) print ('correlation',correlation) print ('pvalue',pvalue)result :
correlation 0.989176319869 pvalue 5.92687594648e-08import matplotlib.pyplot as plt plt.scatter(x,y) plt.show()
Correlation analysis of hierarchical variables
When the measured data is not equidistant or proportional data , But data with hierarchical order ; Or the data obtained is equidistant or proportional data , But the overall distribution from which it comes is not normal , The Pearson correlation coefficient is not satisfied ( Product difference correlation ) The requirements of . At this time, the hierarchical correlation coefficient is used .
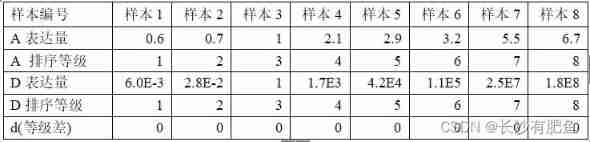
Let's first look at a small experiment , Two genes A、B, Their expression quantity relationship is B=2A, stay 8 The expression values in the samples are as follows :
calculated , Their Pearson correlation coefficient r=1,P-vlaue≈0, From the above, we can see intuitively , If the expression of two genes is linear , There is a significant Pearson correlation .
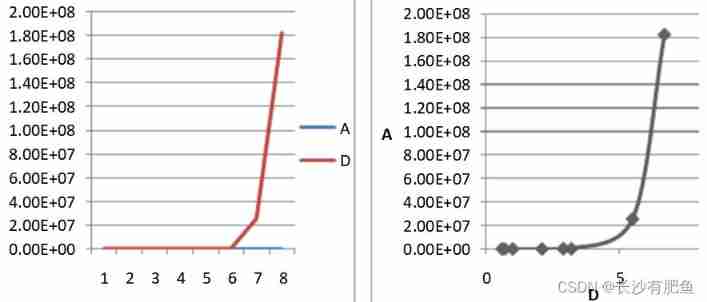
The above is the result of the linear relationship between the two genes . If the two are nonlinear , For example, power function relationship ( The curve relationship ), So what ? Let's try again .
Two genes A、D, Their relationship is D=A^10, stay 8 The expression values in the samples are as follows :
pthon example :
import numpy as np import scipy.stats as stats import scipy x = [0.6,0.7,1,2.1,2.9,3.2,5.5,6.7] y = np.power(x,10) correlation,pvalue = stats.stats.pearsonr(x,y) print ('correlation',correlation) print ('pvalue',pvalue)The result of the calculation is :
correlation 0.765928796314 pvalue 0.0266964972088You can see , gene A、D The correlation coefficient , Both the value and significance have decreased . Pearson correlation coefficient is a kind of linear correlation coefficient , So if the two variables are linear , With the greatest significance . For nonlinear relations ( for example A、D Power function relation of ), Then its detection effect on correlation will decrease .
At this time, we can consider another calculation method of correlation coefficient : Spearman rank correlation .
Spearman rank correlation
When two variable values are arranged or expressed in hierarchical order , The two corresponding populations are not necessarily normally distributed , The sample size is not necessarily greater than 30, Indicates the correlation between these two variables , be called Spearman Level dependent .
To put it simply , That is, no matter how the data of the two variables change , According to what kind of distribution , We only care about the order of each value in the variable . If the corresponding value of two variables , The ranking order within each group is the same or similar , There is a significant correlation .
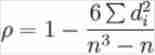
- n Is the number of grades
- d Is the rank difference of two columns of paired variables
Convert the above table into sorting level
Using Spearman rank correlation calculation A、D Correlation of gene expression , The result is :r=1,p-value = 4.96e-05
The significance of Spearman rank correlation is obviously higher than that of Pearson correlation . This is because although the expression of the two genes is nonlinear , But the order of the two gene expression amounts in all samples is exactly the same , Because there is a very significant Spearman rank correlation .
python:
x = [10.35, 6.24, 3.18, 8.46, 3.21, 7.65, 4.32, 8.66, 9.12, 10.31] y = [5.13, 3.15, 1.67, 4.33, 1.76, 4.11, 2.11, 4.88, 4.99, 5.12] correlation,pvalue = stats.stats.spearmanr(x,y) print ('correlation',correlation) print ('pvalue',pvalue)result :
correlation 1.0 pvalue 6.64689742203e-64Spearman example
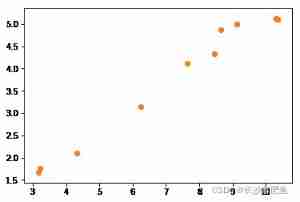
10 The scores of the potential learning ability test and self-study ability test of senior three students are shown in the table below , Ask how the two are related ?
Calculate the rank correlation coefficient
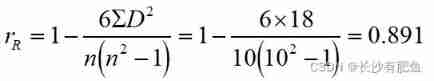
Significance test of rank correlation coefficient
- The method is the same as that of the product difference correlation coefficient test
10 The correlation coefficient between students' learning potential ability and self-study ability test scores is 0.891, Generally speaking , Whether there is a correlation between the two ?
Calculate the value of the test statistic :
Therefore, there is a high positive correlation between students' learning potential ability and self-study ability .
Kendall harmony coefficient (Kendall)
When more than one ( More than two ) Variable values are arranged in hierarchical order or expressed in hierarchical order , A quantity that describes the degree of consistency between these variables , It's called Kendall's harmony coefficient . It is often used to indicate the degree of consistency between several raters who grade the scores of the same group of students successively .
When the same evaluator does not have the same rating , Calculation formula :
- N— The number of people who were rated ;
- K— The number of raters or the number of criteria on which the score is based ;
- S— The sum of the grades of each evaluated object Ri Sum of squares of deviations from the mean of all these sums
When the raters agree completely ,S Get the maximum , The harmony coefficient is actually obtained S The ratio of its maximum possible value , so 0≤W≤1.
When the same evaluator has the same rating , Calculation formula
- mi For the first time i The number of repeated grades in the evaluation results of evaluators .
- nij For the first time i Of the evaluation results of the first evaluator j The number of identical levels of multiple duplicate levels .
- There are no evaluators of the same grade for the evaluation results ,Ti = 0, Therefore, only evaluators with the same level of evaluation results need to calculate Ti.
example 1: When the same evaluator does not have the same rating
A school carries out a student essay competition , please 6 A teacher commented on the selected 6 This paper is rated as an award-winning grade , The results are shown in the table below , Try to calculate 6 Evaluation results of Teachers kandall Harmony coefficient .
Because each grading teacher is right 6 There is no same grade for all papers :

from W=0.87 indicate 6 The evaluation results of teachers are quite consistent
example 2: When the same evaluator has the same rating
3 Experts are right 6 The scores of psychological papers are converted into grades as shown in the table below , Try to calculate the Kendall harmony coefficient of the expert evaluation results
Because expert a 、 C: Yes 6 Papers have the same rating
from W=0.85 It can be seen that the expert evaluation results are relatively consistent
Significance test of Kendall's harmony coefficient
Number of raters (k) stay 3-20 Between , Evaluated person (N) stay 3-7 Between time , having evidence or referent sources 《 Kendall harmony coefficient (W) Significance threshold table 》, test W Whether the significance level is reached . If actually calculated S Greater than k、N The same critical value in the table , be W Reach a significant level .
When K=6 N=6, The inspection levels obtained by looking up the table are α = 0.01,α = 0.05 The critical values are S0.01 = 282.4,S0.05 = 221.4, Are less than the actual S=546, so W Reach a significant level , Think 6 A teacher is right 6 The evaluation of this paper is quite consistent .
When the reviewer n>7 when , You can use the following x2 Statistics on W Whether it reaches the significant level is tested .
x1 = [10, 9, 8, 7, 6] x2 = [10, 8, 9, 6, 7] tau, p_value = stats.kendalltau(x1, x2) print ('tau',tau) print ('p_value',p_value)tau 0.6 p_value 0.141644690295
Quality correlation analysis
Quality correlation means that a variable is qualitative , Another variable is quantity , The correlation between these two variables . Such as IQ 、 Subject score 、 height 、 Weight, etc. are variables expressed as quantity , Men and women 、 Good and bad 、 Pass and fail are qualitative variables .
The correlation between quality and quantity mainly includes two columns of correlation 、 Point two column correlation 、 Multi series correlation .
Two column correlation
When both variables are normal continuous variables . One of the variables is artificially divided into binary variables ( For example, according to a certain standard, the subject examination scores belonging to normal continuous variables are divided into pass and fail , Admission and non Admission , Divide the test results of a sport into pass and fail , Compliance and non-compliance , Divide health into good and bad , wait ), Indicates the correlation between these two variables , It is called two column correlation .
Two columns of relevant service conditions :
- Both variables are continuous , And the overall normal distribution , Or the overall distribution is close to normal , At least unimodal symmetric distribution .
- There is a linear relationship between the two variables .
- Dichotomous variables are artificially divided , The dividing point shall be as close to the median value as possible .
- The sample size should be greater than 80.
Two related examples :
10 The scores of candidates are as follows , Including the total score and a question and answer , Try to find the distinction of the question (6 The score above is passed , Include 6 branch )
Q & A questions , Artificially divided into two categories , Pass and fail , Two columns of correlation shall be required .
Slightly higher discrimination
Point two column correlation
When one of the two variables is a normal continuous variable , The other is the real binary nominal variable ( for example , Men and women , Married and unmarried , Color blindness and non color blindness , Life and death , wait ), At this time , Indicates the correlation between these two variables , It is called point two column correlation .
Point two column related examples :
Yes 50 Multiple choice questions , Each question 2 branch , Yes 20 The total score of the person and the situation of the fifth question , How relevant is the fifth question to the total score .
p( The proportion of students who answered correctly ) = 10/20 = 0.5 ,q = 1-p = 0.5
The correlation coefficient is high , The fifth question is consistent with the total score ( High discrimination )
x = [1,0,0,0,0,0,0,1,1,1,1,0,1,1,1,1,1,0,0,0] y = [84,82,76,60,72,74,76,84,88,90,78,80,92,94,96,88,90,78,76,74] stats.pointbiserialr(x, y)PointbiserialrResult(correlation=0.7849870641173371, pvalue=4.1459279734903919e-05)
Quality correlation analysis
Both variables are divided into several categories by quality , The correlation between these two variables is called quality correlation .
Such as , One variable is divided into men and women by sex , The other variable is divided into pass and fail according to subject scores ; And so on , One variable is divided into focus and non focus by school category , The other variable is divided into excellent students according to subject scores 、 good 、 in 、 Bad , wait .
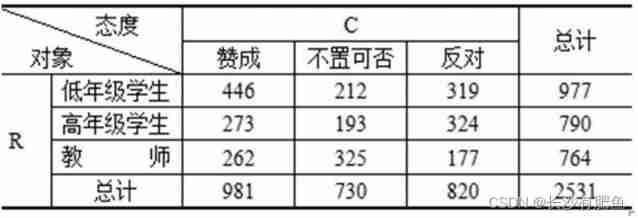
2531 A sample survey was conducted among students and teachers , Calculate the correlation coefficient between respondents and attitudes , And statistical significance test
φ relevant
In order to study the relationship between young college students' attitudes towards gender and psychological tests , Selected 170 A young man took a psychological test , Calculate the effect of gender on test attitude φ The correlation coefficient
Partial correlation analysis
In a geographic system composed of multiple elements , Without considering the influence of other factors , And the closeness of the relationship between the two elements , This is called partial correlation . A statistic used to measure the degree of partial correlation , Called partial correlation coefficient .
When analyzing variables x1 and x2 When the net correlation between , When controlling variables x3 After the linear action of ,x1 and x2 The first-order partial correlation coefficient between is defined as :
For a certain four geographical elements x1,x2,x3,x4 Of 23 Sample data , After calculation, the following single correlation coefficient matrix is obtained :
Partial partial correlation coefficient can be obtained by calculation :
Properties of partial correlation coefficient
- The distribution range of partial correlation coefficient is -1 To 1 Between
- The greater the absolute value of the partial correlation coefficient , Indicates that the greater the degree of partial correlation
- The absolute value of partial correlation coefficient must be less than or at most equal to the complex correlation coefficient obtained from the same series of data , namely R1·23≥|r12·3|
Significance test of partial correlation coefficient
- n: Sample size
- k Is the number of variables excluded
- r Is the partial correlation coefficient
When there is 3 Element time , There are three partial correlation coefficients , It is called first-order partial correlation coefficient
When there is 4 Element time , There are six partial correlation coefficients , They are called second-order partial correlation coefficients
Complex correlation coefficient
Reflect the relationship between several elements and one element The degree of complex correlation . The complex correlation coefficient is between 0 To 1 Between .
The larger the complex correlation coefficient , Indicates that the element ( Variable ) The closer the correlation between . The complex correlation coefficient is 1, Indicates complete correlation ; The complex correlation coefficient is 0, It means nothing at all .
The complex correlation coefficient must be greater than or at least equal to the absolute value of the single correlation coefficient .
Measure a variable y, When there are two independent variables :
When there are three independent variables :

example :
In the example above , If the x4 As the dependent variable ,x1,x2,x3 Independent variable , Try to calculate x4 And x1,x2,x3 The complex correlation coefficient between .
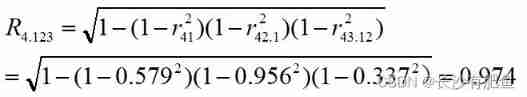
边栏推荐
- Cgb2201 preparatory class evening self-study and lecture content
- Qtoolbutton available signal
- D29:post Office (post office, translation)
- Arc135 partial solution
- 炒股開戶傭金優惠怎麼才能獲得,網上開戶安全嗎
- Powerful blog summary
- Gossip about redis source code 79
- A preliminary study on the middleware of script Downloader
- Introduction to the gtid mode of MySQL master-slave replication
- X Opencv feature point detection and matching
猜你喜欢

Ningde times and BYD have refuted rumors one after another. Why does someone always want to harm domestic brands?

Tencent interview: can you find the number of 1 in binary?
Hcip day 15 notes

Design of logic level conversion in high speed circuit

Recursive least square adjustment

How will the complete NFT platform work in 2022? How about its core functions and online time?

X Opencv feature point detection and matching
![[network security] what is emergency response? What indicators should you pay attention to in emergency response?](/img/ff/c733ffbb922760910ab09af3ae2886.jpg)
[network security] what is emergency response? What indicators should you pay attention to in emergency response?

Investment demand and income forecast report of China's building ceramics industry, 2022-2028
Apple released a supplementary update to MacOS Catalina 10.15.5, which mainly fixes security vulnerabilities
随机推荐
D25:sequence search (sequence search, translation + problem solving)
Op amp related - link
2022 a special equipment related management (elevator) examination questions and a special equipment related management (elevator) examination contents
Gossip about redis source code 80
Ningde times and BYD have refuted rumors one after another. Why does someone always want to harm domestic brands?
Pyqt5 sensitive word detection tool production, operator's Gospel
Bufferpool caching mechanism for executing SQL in MySQL
finalize finalization finally final
Gossip about redis source code 77
[BSP video tutorial] stm32h7 video tutorial phase 5: MDK topic, system introduction to MDK debugging, AC5, AC6 compilers, RTE development environment and the role of various configuration items (2022-
How to quickly build high availability of service discovery
[untitled]
How to solve the "safe startup function prevents the operating system from starting" prompt when installing windows10 on parallel desktop?
Yyds dry goods inventory [practical] simply encapsulate JS cycle with FP idea~
33 restrict the input of qlineedit control (verifier)
Analysis on the scale of China's smart health industry and prediction report on the investment trend of the 14th five year plan 2022-2028 Edition
Gossip about redis source code 75
leetcode-43. String multiplication
D30:color tunnels (color tunnels, translation)
Ppt image processing