当前位置:网站首页>CodeCraft-22 and Codeforces Round #795 (Div. 2)D,E
CodeCraft-22 and Codeforces Round #795 (Div. 2)D,E
2022-07-02 15:02:00 【Not Zhang Pangpang】
List of articles
D.Max GEQ Sum
The question :
I'll give you a length of n ( 1 ≤ 2 ∗ 1 0 5 ) n(1 \leq 2*10^5) n(1≤2∗105) Array of a a a, Whether it is satisfied for any i , j ( 1 ≤ i ≤ j ≤ n ) i,j(1 \leq i \leq j \leq n) i,j(1≤i≤j≤n), Guarantee
max ( a i , a i + 1 , . . . , a j − 1 , a j ) ≥ a i + a i + 1 + . . . + a j 1 + a j \max(a_i,a_{i+1},...,a_{j-1},a_j) \geq a_i+a_{i+1}+...+a_{j_1}+a_j max(ai,ai+1,...,aj−1,aj)≥ai+ai+1+...+aj1+aj Ideas :
adopt Monotonic stack , We can find a number left / The position of the first larger number on the right , So we can know that the maximum value is a i a_i ai The value range of the left and right boundaries of time
In this range , as long as ∑ a \sum a ∑a The maximum value of is less than max a \max a maxa That is to meet the requirements , So record a prefix and , The segment tree is used to maintain the maximum and minimum values of the interval , The maximum value is calculated by subtracting the minimum value on the left from the maximum value on the right ∑ a \sum a ∑a
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef long long ll;
const int maxn=2e5+7;
int n,a[maxn],b[maxn],l[maxn],r[maxn];
struct tree
{
int l,r,mx,mn;
int mid()
{
return (l+r)/2;
}
}tre[maxn<<2];
void pushup(int num)
{
tre[num].mx=max(tre[2*num].mx,tre[2*num+1].mx);
tre[num].mn=min(tre[2*num].mn,tre[2*num+1].mn);
}
void build(int num,int l,int r)
{
tre[num].l=l,tre[num].r=r;
if(l==r)
{
tre[num].mx=tre[num].mn=a[l];return;
}
int mid=tre[num].mid();
build(2*num,l,mid);
build(2*num+1,mid+1,r);
pushup(num);
}
int query_max(int num,int l,int r)
{
if(tre[num].l==l && tre[num].r==r)
return tre[num].mx;
int mid=tre[num].mid();
if(l>mid)
return query_max(2*num+1,l,r);
else if(r<=mid)
return query_max(2*num,l,r);
else
return max(query_max(2*num,l,mid),query_max(2*num+1,mid+1,r));
}
int query_min(int num,int l,int r)
{
if(tre[num].l==l && tre[num].r==r)
return tre[num].mn;
int mid=tre[num].mid();
if(l>mid)
return query_min(2*num+1,l,r);
else if(r<=mid)
return query_min(2*num,l,r);
else
return min(query_min(2*num,l,mid),query_min(2*num+1,mid+1,r));
}
signed main()
{
int T;scanf("%lld",&T);
while(T--)
{
scanf("%lld",&n);
for(int i=1;i<=n;i++)
{
scanf("%lld",&b[i]);
}
stack<int>s;
for(int i=1;i<=n;i++)
{
while(!s.empty() && b[i]>=b[s.top()]) s.pop();
if(s.size()==0) l[i]=0;
else l[i]=s.top();
s.push(i);
}
while(!s.empty()) s.pop();
for(int i=n;i>=1;i--)
{
while(!s.empty() && b[s.top()]<=b[i]) s.pop();
if(s.size()==0) r[i]=n+1;
else r[i]=s.top();
s.push(i);
}
for(int i=1;i<=n;i++) a[i]=a[i-1]+b[i];
a[n+1]=a[n];
build(1,0,n+1);
int ok=1;
for(int i=1;i<=n;i++)
{
int mn=query_min(1,l[i],i-1);
int mx=query_max(1,i,r[i]-1);
if(mx-mn>b[i])
{
ok=0;break;
}
}
ok?puts("YES"):puts("NO");
}
}
E. Number of Groups
The question :
Here you are. n n n Segment interval , Each interval has colors 0 , 1 0,1 0,1, And length l , r ( 0 ≤ l i ≤ r i ≤ 1 0 9 ) l,r(0≤l_i≤r_i≤10^9) l,r(0≤li≤ri≤109)
If the color of two sections is different , And there are intersections that can be connected with chains , Ask this n n n How many sets will be formed by each interval 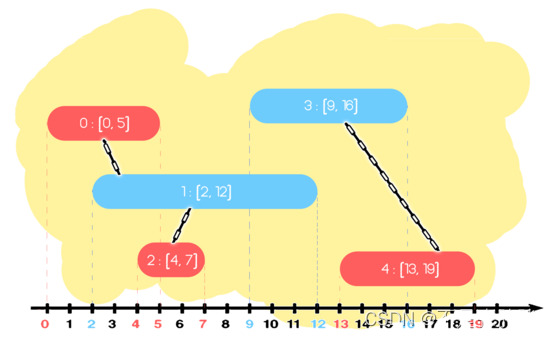
Ideas :
It is obvious that the title of the joint search set , The problem is how to optimize some time
One of my thoughts is : Split all sections left and right to sort , use s e t set set Storage , If it's the left endpoint , And put another color s e t set set Connect to it , Put in s e t set set, Otherwise delete from .
The reason why the speed is too slow is that some edges that are already in the same set are repeatedly connected , So we delete the same color intervals that have been connected together , Only the farthest right endpoint
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+7;
int fa[maxn],n;
int find(int x){
if(x==fa[x]) return fa[x]; return fa[x]=find(fa[x]);}
void lianjie(int x,int y){
int px=find(x),py=find(y);fa[px]=py;}
struct node
{
int l,r,id;
bool operator < (const node& n1)const
{
if(n1.r==r && n1.l==l) return n1.id>id;
if(n1.r==r) return n1.l>l;
return n1.r>r;
}
}a[maxn];
int main()
{
int T;scanf("%d",&T);
while(T--)
{
int n;scanf("%d",&n);
vector<tuple<int,int,int,int,int>>v;
for(int i=1;i<=n;i++)
{
int col,l,r;
fa[i]=i;scanf("%d%d%d",&col,&l,&r);
v.push_back({
l,1,r,col,i});v.push_back({
r,2,l,col,i});
}
sort(v.begin(),v.end());
multiset<node>s[2];
for(int i=0;i<v.size();i++)
{
vector<tuple<int,int,int,int>>del;
auto [x,y,z,col,id]=v[i];
if(y==1)
{
for(auto [l,r,id2]:s[col^1])
{
if(x<=r)
{
del.push_back({
l,r,id2,col^1});
lianjie(id,id2);
}
}
if(del.size()) del.pop_back();
s[col].insert({
x,z,id});
}
else
{
del.push_back({
z,x,id,col});
// printf("---\n");
}
for(auto [x,y,z,c]:del)
{
s[c].erase({
x,y,z});
}
}
int ans=0;
for(int i=1;i<=n;i++) if(fa[i]==i) ans++;//printf("i=%d \n",i);
printf(" %d\n",ans);
}
}
边栏推荐
- LeetCode 2310. 个位数字为 K 的整数之和
- C语言中的printf函数和scanf函数
- Implement a server with multi process concurrency
- Wechat applet uses towxml to display formula
- 【C语言】详解指针的初阶和进阶以及注意点(1)
- vChain: Enabling Verifiable Boolean Range Queries over Blockchain Databases(sigmod‘2019)
- 【apipost】使用教程
- Arithmetic operations and related exercises in C language
- taobao. trades. sold. Get query the transaction data that the seller has sold (according to the creation time), Taobao store sales order query API interface, Taobao R2 interface, Taobao oauth2.0 trans
- 检查密码
猜你喜欢

forEach的错误用法,你都学废了吗

Socket and socket address

LeetCode 2310. The number of digits is the sum of integers of K

About text selection in web pages and counting the length of selected text

Simple verification code generator for 51 single chip microcomputer experiment
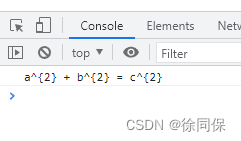
MathML to latex
![[development environment] install the visual studio community 2013 development environment (download the installation package of visual studio community 2013 with update 5 version)](/img/7b/2c471c070a3faa981f70136603495a.jpg)
[development environment] install the visual studio community 2013 development environment (download the installation package of visual studio community 2013 with update 5 version)
Fatal: unsafe repository is owned by someone else

【NOI模拟赛】刮痧(动态规划)

Introduction to C language -- array
随机推荐
Advanced C language (learn malloc & calloc & realloc & free in simple dynamic memory management)
2、const 型指针
C# richTextBox控制显示最大行数
传感器数据怎么写入电脑数据库
Makefile separates file names and suffixes
kityformula-editor 配置字号和间距
taobao. logistics. dummy. Send (no logistics delivery processing) interface, Taobao store delivery API interface, Taobao order delivery interface, Taobao R2 interface, Taobao oau2.0 interface
Huawei interview question: no palindrome string
求轮廓最大内接圆
taobao.trade.get( 获取单笔交易的部分信息),淘宝店铺订单接口,淘宝oAuth2.0接口,淘宝R2接口代码对接分享
taobao.trades.sold.get-查询卖家已卖出的交易数据(根据创建时间),淘宝店铺卖出订单查询API接口,淘宝R2接口,淘宝oAuth2.0交易接口代码分享
Wechat applet uses towxml to display formula
C语言实现N皇后问题
3. Function pointers and pointer functions
【apipost】使用教程
[Space & single cellomics] phase 1: single cell binding space transcriptome research PDAC tumor microenvironment
Tmall product details interface (APP, H5 end)
taobao.logistics.dummy.send( 无需物流发货处理 )接口,淘宝店铺发货API接口,淘宝订单发货接口,淘宝r2接口,淘宝oAu2.0接口
天猫商品详情接口(APP,H5端)
Large top heap, small top heap and heap sequencing