大顶堆、小顶堆与堆排序

堆结构是一种特殊的逻辑结构，通过堆排序算法可以将无序堆经O(logn)时间排序为一个大顶堆或小顶堆，从而快速获取最大值和最小值。

1.堆的物理结构和逻辑结构

堆的逻辑结构是一颗完全二叉树，而内存中实际的物理结构是一个顺序数组。

完全二叉树是一种每一层都是从左往右放值直到把该层放满才会增长至更深层的结构。

堆的数组到堆结构的映射关系满足：数组中第i个元素的左孩子为第2*i+1的元素，右孩子为第2*i+2的元素，父节点为第(i-1)/2 （取整数位，0位的父节点是自己）的元素。

堆的逻辑结构

堆的物理结构

 

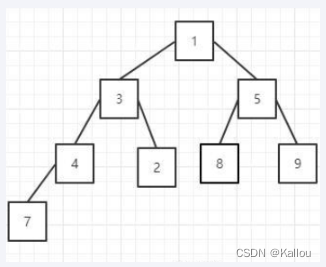
 2.大顶堆与小顶堆

大顶堆即对于堆中任何一颗子树来说，该子树的最大值一定是其根节点。

大顶堆

小顶堆即对于堆中任何一颗子树来说，该子树的最小值一定是其根节点。

小顶堆

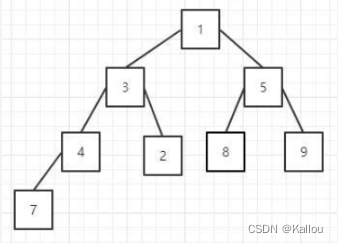
 3.堆结构的相关函数实现

该示例是一个可对无序堆进行堆排序变为大顶堆的程序，各函数意义详见注释。（程序未给出主函数，如需运行请自行编写）

/*………………………………………堆排序O(logN)………………………………………*/
//该函数为heapinsert的一个重载版本
//该版本中的三个参数，vec表示一个已经是大根堆的数组，size表示数组中的有效位，num为待插入元素
template<typename T>
void heapinsert(vector<T>& vec, int size,T num)
{
	vec.push_back(num);
	while (vec[size] > vec[(size - 1) / 2])
	{
		swap(vec[(size - 1) / 2], vec[size]);
		size = (size - 1) / 2;
	}
	return;
}
//该函数为heapinsert的一个重载版本
//该版本中的两个参数，vec表示待插入的堆，size表示本次插入中堆的有效位
template<typename T>
void heapinsert(vector<T>& vec, int size)
{
	while (vec[size] > vec[(size - 1) / 2])
	{
		swap(vec[(size - 1) / 2], vec[size]);
		size = (size - 1) / 2;
	}
	return;
}
//堆下潜
template<typename T>
void _heapify(vector<T>& vec,int size)
{
	int index = 0;
	int left = index * 2 + 1;

	while (left < size)
	{
		//该句用以判断左右孩子哪个大，返回较大的那个孩子的下标
		//A?B:C的语法规则是？前为真则返回B假则返回C，
		//在该语句中如果右孩子越界，则&&左边为假，？前就为假，返回left；
		//不越界就继续往后看，判断左右孩子孰大孰小。
		int largest = left + 1 < size && vec[left] < vec[left + 1] ? left + 1 : left;
		if (vec[index] < vec[largest])
		{
			swap(vec[index], vec[largest]);
			index = largest;
			left = index * 2 + 1;
		}
		else
			break;

	}
}
//弹出最大值
template<typename T>
T pop_max(vector<T>& vec, int size)
{
	//将堆顶元素与堆尾交换
	swap(vec[0], vec[size - 1]);
	//对堆尾之前（不包括堆尾）的堆进行heapify操作
	_heapify(vec,size-1);
	return vec[size-1];
}
//堆排序
template<typename T>
void heapSort(vector<T>& vec)
{
	if (vec.empty() || vec.size() < 2)
		return;
	//将输入数组变为大根堆
	for (int i = 0; i < vec.size(); ++i)
		heapinsert(vec,i);
	for (int i = vec.size(); i > 0; --i)
		pop_max(vec, i);
}

堆排序每次都是与父节点比较，如果比父节点大就上浮一层，因此上浮的最大次数就是堆的层数，堆又是一个完全二叉树，根据完全二叉树的性质可知其层数与元素个数的关系是2^h-1，h为层数，因此易得堆排序的时间复杂度为O(logn)。

堆下潜的意义是在取出堆的根节点后，对剩余的节点进行排序使之重新按照原有规则恢复，其时间复杂度也是O(logn)。

因此一次完整的无序堆取出最大值（最小值）的时间复杂度是O(2logn)，常数项可忽略，最后依然是O(logn)