当前位置:网站首页>为什么四个字节的float表示的范围比八个字节的long要广
为什么四个字节的float表示的范围比八个字节的long要广
2022-08-02 13:31:00 【学编程的小趴菜】
Java中浮点数分为两种:
种类名称 存储大小 取值范围
float(单精度) 4字节(32bit)
-3.403E38 ~ 3.403E38
double(双精度) 8字节(64bit)
-1.798E308 ~ 1.798E308
存储结构
浮点数的存储分三个部分:
符号位
指数位
尾数位(有效数字)
单精度浮点数32位=1位符号位+8位指数位+23位有效数字
双精度浮点数64位=1位符号位+11位指数位+52位有效数字
计算机存储浮点数
符号位:1表示负值,0表示正值
指数位:float的指数范围8位(为-128~+127),而double的指数范围11位(为-1024~+1023),并且指数位是按补码的形式来划分的。
其中负指数决定了浮点数所能表达的绝对值最小的非零数;而正指数决定了浮点数所能表达的绝对值最大的数,也即决定了浮点数的取值范围。
尾数位:float和double的精度是由尾数的位数来决定的。浮点数在内存中是按科学计数法来存储的,其整数部分始终是一个隐含着的“1”,由于它是不变的,故不能对精度造成影响。
float:2^23 = 8388608,一共七位,由于最左为1的一位省略了,这意味着最多能表示8位数: 2*8388608 = 16777216 。有8位有效数字,但绝对能保证的为7位,即 float的精度为7~8位有效数字;double:2^52 = 4503599627370496,一共16位,double的精度为16~17位。
IEEE 浮点标准
根据IEEE 浮点标准,任意一个二进制浮点数N可以表示成下面的形式:
32位浮点数
N = (-1)^s × (1.M )× 2^(E-127)
64位浮点数
N = (-1)^s × (1.M )× 2^(E-1023)
符号(sign) s表示符号位,当s=0,N为正数;当s=1,N为负数。
尾数(significand) M是一个二进制小数,1≤M<2。
指数位(exponent) E的作用是对浮点数加权,这个权重是2的E次幂(可能是负数)
E阶码占用8位,阶符采用隐含方式,,即采用移码方法来表示正负指数。移码方法对两个指数大小的比较和对阶操作都比较方便,因为阶码域值大者其指数值也大。采用这种方式时,将浮点数的指数真值e变成阶码E时,应将指数e加上一个固定的偏移值127(01111111),即E=e+127。
基本数据类型(4类8种),整数类型,浮点类型,字符型,布尔型。
整数类型:
long 8字节(64bit) -2^63 ---- 2^63-1
32位浮点数
float 四字节(32bit) -2^127--2^127
整数与浮点数在底层存储之间有所不同,所以4位的float比8位的long表示的范围更大
边栏推荐
- Article 48 - Analysis of timestamp2 parameters【2022-08-01】
- How to turn off hardware acceleration [easy to understand]
- 图论之Prim,最小生成树该怎么解?
- Enterprise Network Planning Based on Huawei eNSP
- k8s之KubeSphere部署有状态数据库中间件服务 mysql、redis、mongo
- RISC-V 指令格式和6种基本整数指令
- 【C语言】剖析函数递归(2)
- 第48篇-timestamp2参数分析【2022-08-01】
- 【C语言】虐打循环练习题(2)
- 读《IDEO,设计改变一切》有感
猜你喜欢
鲁大师7月新机性能/流畅榜:骁龙8+正面对决天玑9000+,性能跑分突破123万!

【C语言】夏日一题 —— 如何判断素数?
【C语言】细品分支结构——if-else语句

How to do short video food from the media?5 steps to teach you to get started quickly

Mysql索引详解(图文并茂)
线程安全问题及关键字synchronized,volatile
ThinkPHP 5.1反序列化分析和poc
![[C language] Analysis of function recursion (2)](/img/b1/9baa60a69d41a1823ed92001d1b0a0.png)
[C language] Analysis of function recursion (2)
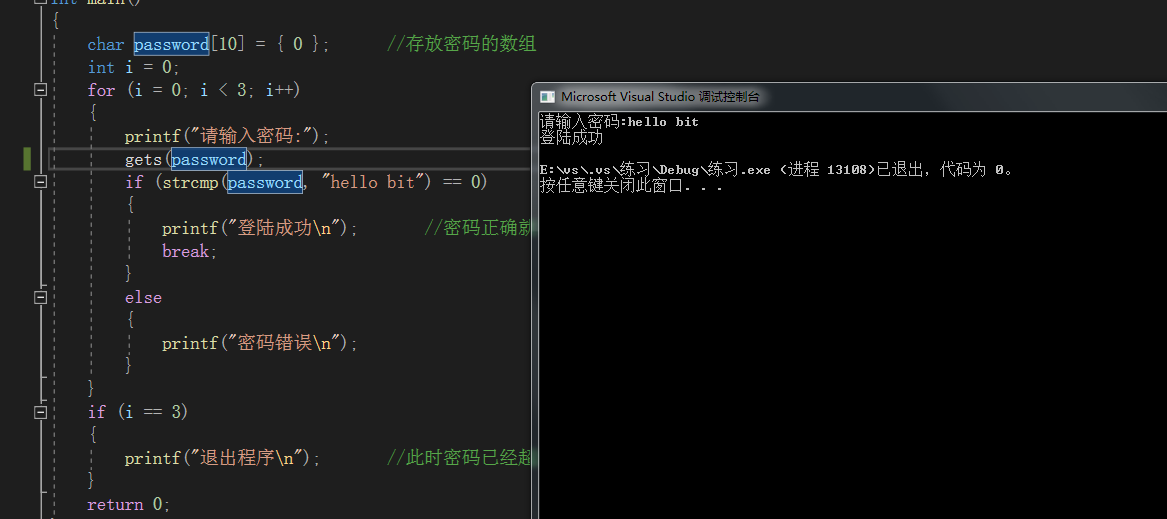
【C语言】虐打循环练习题(2)
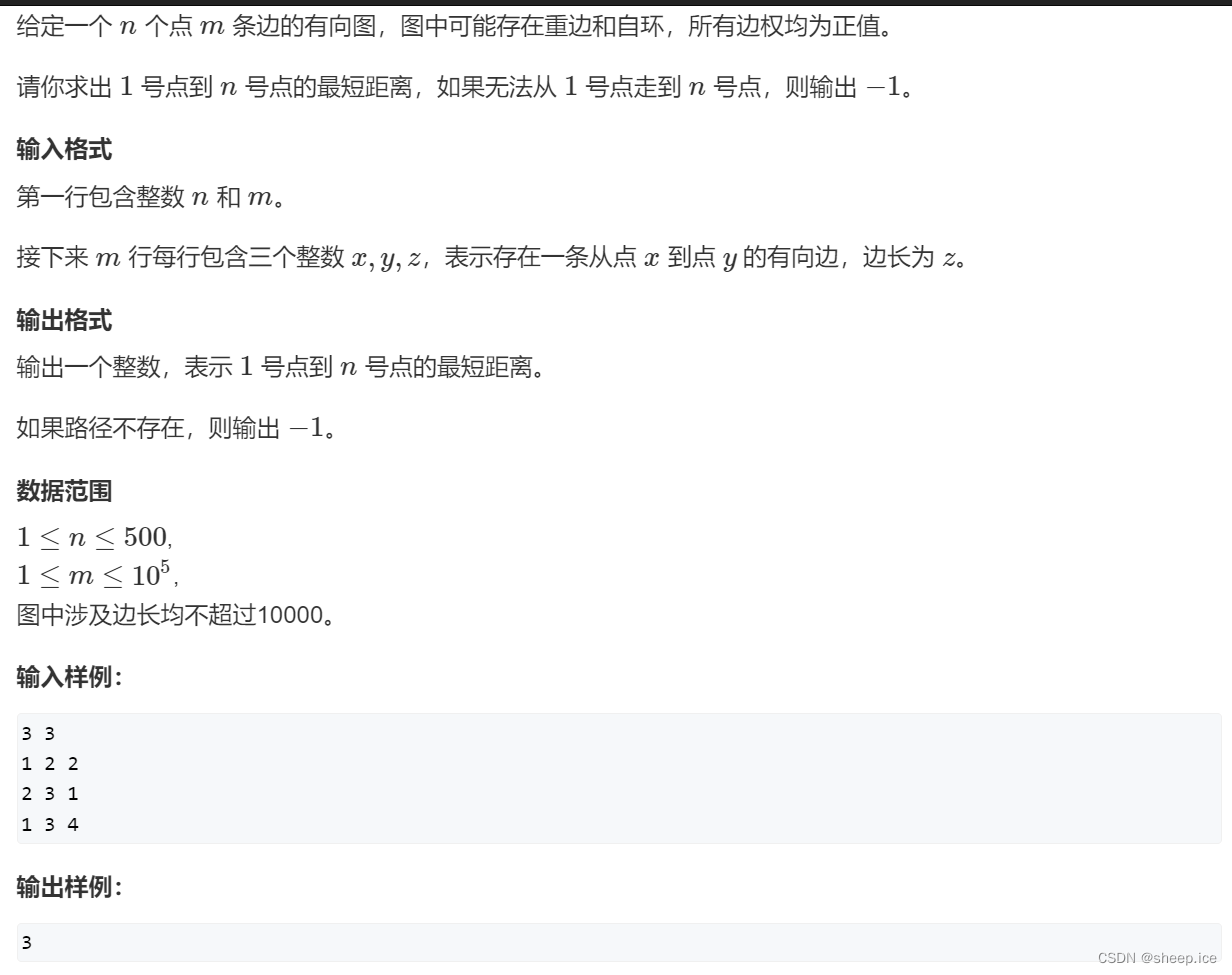
Do you know Dijkstra of graph theory?
随机推荐
“二舅”火了,自媒体短视频“爆火”的基本要素,你知道吗?
【C语言】手把手带你写游戏 —— 猜数字
节省50%成本!京东云重磅发布新一代混合CDN产品
Selenium本地打开远程浏览器
自媒体创作怎样提高原创度,打造爆款作品?
Wireless vibrating wire acquisition instrument remote modification method
Redis全部
qt 编译报错 No rule to make target
吾爱第三课-修改版权和资源
scrapy框架初识1
Summer training camp-week2 graph theory
【C语言】明解数组(1)
Reading IDEO, Design Changes Everything
Word | 关于删除分节符(下一页)前面的版式就乱了解决方案
方正璞华“劳动人事法律自助咨询服务平台”在武汉武昌区投入使用!
面试SQL语句,学会这些就够了!!!
Redis all
Based on the flask mall administrator functions
Introduction to Graph Neural Networks (GNN) "Recommended Collection"
FreeBSD bnxt以太网驱动源码阅读记录三: