当前位置:网站首页>扩展欧几里得求逆元实例
扩展欧几里得求逆元实例
2022-08-03 15:33:00 【PolarDay.】
扩展欧几里得求逆元实例
首先说一下逆元的定义
存在一个数a使得ax对y进行取余运算,得到的值是1,则称a是x的逆元。在数学中记做:a * x = 1(mod p)
例如x = 4,y = 11,3x = 1(mod y),3 × 4 = 12,12 mod 11 = 1 , 3就是x的逆元。
对于求逆元这一操作在计算机领域主要用于非对称加密,如我们常见的RSA加密算法等。
那应该求得这个逆元呢,我们知道,再求两个数的最大公约数的时候可以用欧几里得算法。
在欧几里得算法中,通过辗转相除,当余数为0的时候最后的除数就是两个数的最大公约数。
而在其扩展算法中,我们已知两个数的最大公约数,我们已知 ax = 1(mod p),
展开就是 ax mod p = 1,首先我们先求 p = x1 * a + p1,然后 p = a,a = p1,迭代下去直到pi = 1(i表示出了i次)为止
然后就可以得出 1 = p - xi * a,此时的a和p已经不是我们初始的a和p了,我们需要往前推,推到 1= xa + yp 为止,此时得出的x就是a的逆元,当然如果逆元x为负数,或者比p大,要对其就行取余操作。
举个例子 11 = 1(mod 20)求11的逆元
20 = 1 × 11 + 9 //注释:此时x1 = 1, a = 11,p = 20,p1 = 9,执行p = a,a = p1
11 = 1 × 9 + 2 //注释:x2 = 1,a = 9,p2 = 2。
9 = 4 × 2 + 1 //注释:p3 = 1
此时得到:1 = 9 - 2 × 4,开始往前推直到推出 1= xa + yp
从上述式子中可以得知 9 = 20-11
1 = 20 - 11 - 2 × 4
同时 2 = 11 -9
1 = 20 -11 -4 × (11-9)
已知 9 = 20 - 11
1 = 20 -11 -4 × (11-(20-11))
1 = 20 -11 -4 × (11-20+11)
合并同类项得
1 = 5 × 20 - 9 × 11
1 = y × 20 + x × 11
x为a的逆元 -9
-9对p取余为11
综上11模20的逆元为11
验证 11 × 11 = 121,121 mod 20 = 6 — 1
到此 计算结束
边栏推荐
- leetcode:899. 有序队列【思维题】
- NFT盲盒挖矿DAO智能合约dapp系统开发详情
- PHP中高级面试题 – 第一天
- 2021年12月电子学会图形化一级编程题解析含答案:放学
- 每日练习------有10个数字要求分别用选择法从大到小输出
- 2021年12月电子学会图形化三级编程题解析含答案:跳高比赛
- cnpm 安装成功后提示不是内部和外部命令,也不是可运行的命令解决方案
- 2021年12月电子学会图形化四级编程题解析含答案:棕熊大战
- Internship Road: Documenting Confusion in My First Internship Project
- LyScript 验证PE程序开启的保护
猜你喜欢

After the cnpm installation is successful, the prompt is not an internal and external command, nor is it a runnable command solution

How to play deep paging with hundreds of millions of data?Compatible with MySQL + ES + MongoDB
LyScript 验证PE程序开启的保护
MATLAB gcf figure save image with black background/transparent background

红蓝对抗经验分享:CS免杀姿势
The general trend, another key industry related to Sino-US competition, has reached a critical moment
A new round of competition for speech recognition has started. Will natural dialogue be the next commanding height?
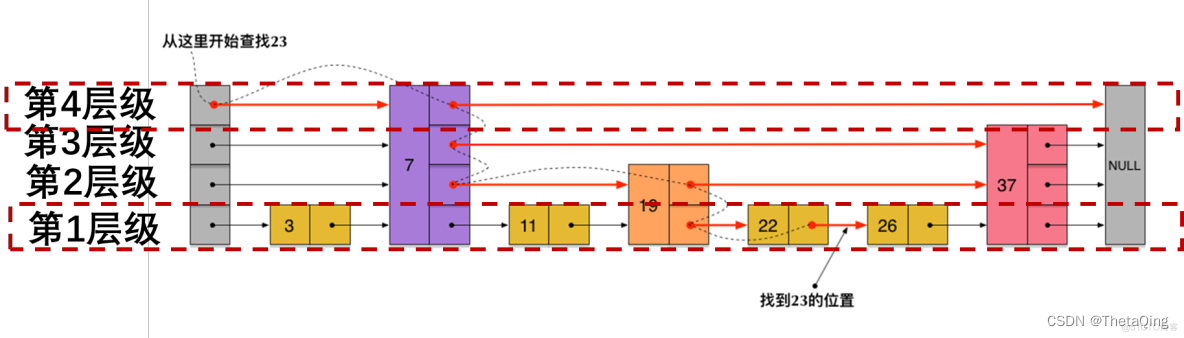
力扣1206. 设计跳表--SkipList跳表是怎么跳的?

方舟生存进化开服需要多少钱
深入浅出Flask PIN
随机推荐
兔起鹘落全端涵盖,Go lang1.18入门精炼教程,由白丁入鸿儒,全平台(Sublime 4)Go lang开发环境搭建EP00
程序员面试必备PHP基础面试题 – 第十八天
Basic knowledge points in js - events
ubiquant量化竞赛
实习路途:记录给我的第一个实习项目中的困惑
分享一款免费OPC UA服务器
16 【过渡 动画】
2021年12月电子学会图形化一级编程题解析含答案:下雨
2021年12月电子学会图形化三级编程题解析含答案:跳高比赛
新一代网状网协议T-Mesh无线通信技术优势介绍
不安装运行时运行.NET程序
新版本的 MaxCompute 中,SQL支持的 LIMIT OFFSET 的语法是什么功能?
Taurus.MVC WebAPI 入门开发教程1:框架下载环境配置与运行(含系列目录)。
js数组方法总结
跨桌面端之组件化实践
无内鬼,来点干货!SQL优化和诊断
NFT盲盒挖矿DAO智能合约dapp系统开发详情
【码蹄集新手村600题】将一个函数定义宏
8月份加密市场的三个关键预期 价格虽向北移动?预计仍将处于动荡之中
自定SvgIcon公用组件