当前位置:网站首页>树状数组模版+例题
树状数组模版+例题
2022-08-05 08:11:00 【9ack!?】
简介
树状数组是一种维护区间和的数据结构,支持单点查询。经过魔改后也可以进行区间修改-单点查询, 区间修改-区间查询。你问为什么没有单点修改, 单点查询?因为数组就可以解决了哈哈。
我这里就不介绍原理了,网上一搜一大把。
基本树状数组
const int maxn = 100;
int a[maxn+5]; // 存放原始数据
int c[maxn+5]; // 存放树状数组
int n; // 存放数据的最大下标
int lowbit(int x) {
return x&(-x);
}
void add(int i, int k) {
while(i <= n) {
c[i] += k;
i += lowbit(i);
}
}
int getsum(int i) {
// 计算从1开始到i(两边都是闭区间)的区间和
int res = 0;
while(i > 0) {
res += c[i];
i -= lowbit(i);
}
}
void init() {
// 创建树的时候调用
for(int i = 1; i <= n; ++i) {
c[i] += a[i];
int j = i + lowbit(i);
if( j <= n) c[j] += c[i];
}
}
// 查询[x, y]
int sum = getsum(y)-getsum(x-1);
区间修改, 单点查询
首先不能直接套用上面的模版,对区间内的每个元素进行单点修改时间复杂度肯定会爆。
思考一下对区间进行修改时的特点,对整个区间进行修改的时候,区间内相邻元素的差值是不变的,所以我们可以用树状数组维护原数组的差分数组,修改的时候只需要对区间的两个端点修改即可。查询某个点的值时,求出差分数组的前缀和即可。
// 这里的函数直接套用上面的模版即可
// [x, y]区间加上k
for(int i = 1; i <= n; ++i) {
// 读入数据
scanf("%d", &a[i]);
update(i, a[i]-a[i-1]);
}
// [x, y]区间加上k
update(x, k);
update(y+1, -k);
int sum = getsum(i); // 这里的getsum变成了对差分数组的前i个元素进行求和, 于是得到的是a[i]
区间修改, 区间查询
这个就更玄学了,这个问题完全可以用线段树来解决,而且明显树状数组能维护的信息不如线段树多。但是线段树的常数要比线段树小,所以在某些条件下还是能解决一些问题的 (就比如下面的例题)
实际代码模版也差不多,但是运用了更加神奇的方法
// 需要维护两个树状数组
const int maxn;
int n, m;
int a[maxn];
int sum1[maxn]; // (D[1] + D[2] + ... D[n]), D是差分数组
int sum2[maxn]; // (1*D[1] + 2*D[2] + .. + n*D[n])
void update(int i, int k) {
int x = i;
while(i <= n) {
sum1[i] += k;
sum2[i] += k*(x-1);
i += lowbit(i);
}
}
int getsum(int i) {
int res = 0, x = i;
while(i > 0) {
res += x*sum1[i] - sum2[i];
i -= lowbit(i);
}
return res;
}
// 读入数据
for(int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
update(i, a[i]-a[i-1]);
}
// [x, y]区间加上k
update(x, k);
update(y+1, -k);
// 求[x, y]区间和
int sum = getsum(y) - getsum(x-1);
//连这一篇都要限流...
边栏推荐
- busybox 知:构建
- 嵌入式系统:基本定时器
- EA谈单机游戏:仍是产品组合中极其重要的部分
- The color of life divine
- Vulnhub target drone: HA_ NARAK
- 基于多块信息提取和马氏距离的k近邻故障监测
- Controller-----controller
- Basic introduction of stack and queue and C language implementation of functions such as creation, destruction, entry and exit, counting the number of elements, viewing elements, etc., as well as stac
- MySQL 数据库 报错 The server quit without updating PID file (/var/lib/mysql/localhost.localdomain.pid)
- tear apart loneliness
猜你喜欢

What is a good movie to watch on Qixi Festival?Crawl movie ratings and save to csv file
Support touch screen slider carousel plugin
Pagoda measurement - building small and medium-sized homestay hotel management source code
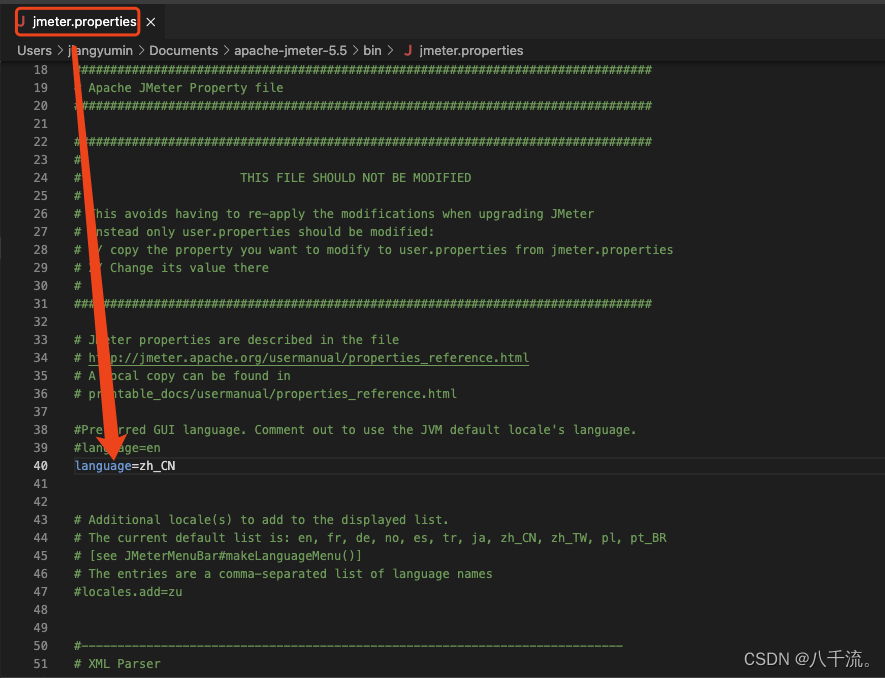
Jmeter永久设置中文界面
爬虫从入门到入牢
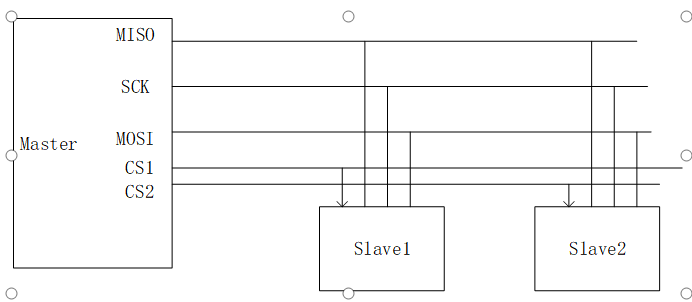
D2--FPGA SPI接口通信2022-08-03

餐饮大单品「真香」,却没有穿透周期的能力
Ethernet Principle
Data source object management Druid and c3p0
关于MP3文件中找不到TAG标签的问题
随机推荐
8.4模拟赛总结
Qt writes custom controls: one of the text spotlight effects
请问my sql如何把两个表的内容集合在一起啊?
P1103 书本整理
Ethernet Principle
星座理想情人
【结构体内功修炼】结构体实现位段(二)
8.4 Summary of the mock competition
How to make pictures clear in ps, self-study ps software photoshop2022, simple and fast use ps to make photos clearer and more textured
Redis cache and existing problems--cache penetration, cache avalanche, cache breakdown and solutions
D2--FPGA SPI interface communication2022-08-03
数据源对象管理Druid和c3p0
常用的遍历map的方法
每一个女孩曾经都是一个没有泪的天使
复现一次循环和两次循环
512色色谱图
[Untitled] Long-term recruitment of hardware engineers-Shenzhen Baoan
Ethernet Principle
SVG大鱼吃小鱼动画js特效
love is a sad song