当前位置:网站首页>统计学习方法(4/22)朴素贝叶斯
统计学习方法(4/22)朴素贝叶斯
2022-06-29 01:05:00 【小帅吖】
朴素贝叶斯(naive bayes)法是基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集,首先基于特征条件独立假设学习输入输出的联合概率分布:然后基于此模型,对给定的输入x,利用贝叶斯定理求出后验概率最大的输出y。朴素贝叶斯法实现简单,学习和预测的效率都很高,是一种常用的方法。
深度之眼课程链接:https://ai.deepshare.net/detail/p_619b93d0e4b07ededa9fcca0/5
代码链接:
https://github.com/zxs-000202/Statistical-Learning-Methods















在推导过程中会有某类样本数目为零进而导致分母为零的状况




后验概率最大化与期望风险最小化等价



# coding=utf-8
# Author:Dodo
# Date:2018-11-17
# Email:[email protected]
''' 数据集:Mnist 训练集数量:60000 测试集数量:10000 ------------------------------ 运行结果: 正确率:84.3% 运行时长:103s '''
import numpy as np
import time
def loadData(fileName):
''' 加载文件 :param fileName:要加载的文件路径 :return: 数据集和标签集 '''
#存放数据及标记
dataArr = []; labelArr = []
#读取文件
fr = open(fileName)
#遍历文件中的每一行
for line in fr.readlines():
#获取当前行,并按“,”切割成字段放入列表中
#strip:去掉每行字符串首尾指定的字符(默认空格或换行符)
#split:按照指定的字符将字符串切割成每个字段,返回列表形式
curLine = line.strip().split(',')
#将每行中除标记外的数据放入数据集中(curLine[0]为标记信息)
#在放入的同时将原先字符串形式的数据转换为整型
#此外将数据进行了二值化处理,大于128的转换成1,小于的转换成0,方便后续计算
dataArr.append([int(int(num) > 128) for num in curLine[1:]])
#将标记信息放入标记集中
#放入的同时将标记转换为整型
labelArr.append(int(curLine[0]))
#返回数据集和标记
return dataArr, labelArr
def NaiveBayes(Py, Px_y, x):
''' 通过朴素贝叶斯进行概率估计 :param Py: 先验概率分布 :param Px_y: 条件概率分布 :param x: 要估计的样本x :return: 返回所有label的估计概率 '''
#设置特征数目
featrueNum = 784
#设置类别数目
classNum = 10
#建立存放所有标记的估计概率数组
P = [0] * classNum
#对于每一个类别,单独估计其概率
for i in range(classNum):
#初始化sum为0,sum为求和项。
#在训练过程中对概率进行了log处理,所以这里原先应当是连乘所有概率,最后比较哪个概率最大
#但是当使用log处理时,连乘变成了累加,所以使用sum
sum = 0
#获取每一个条件概率值,进行累加
for j in range(featrueNum):
sum += Px_y[i][j][x[j]]
#最后再和先验概率相加(也就是式4.7中的先验概率乘以后头那些东西,乘法因为log全变成了加法)
P[i] = sum + Py[i]
#max(P):找到概率最大值
#P.index(max(P)):找到该概率最大值对应的所有(索引值和标签值相等)
return P.index(max(P))
def model_test(Py, Px_y, testDataArr, testLabelArr):
''' 对测试集进行测试 :param Py: 先验概率分布 :param Px_y: 条件概率分布 :param testDataArr: 测试集数据 :param testLabelArr: 测试集标记 :return: 准确率 '''
#错误值计数
errorCnt = 0
#循环遍历测试集中的每一个样本
for i in range(len(testDataArr)):
#获取预测值
presict = NaiveBayes(Py, Px_y, testDataArr[i])
#与答案进行比较
if presict != testLabelArr[i]:
#若错误 错误值计数加1
errorCnt += 1
#返回准确率
return 1 - (errorCnt / len(testDataArr))
def getAllProbability(trainDataArr, trainLabelArr):
''' 通过训练集计算先验概率分布和条件概率分布 :param trainDataArr: 训练数据集 :param trainLabelArr: 训练标记集 :return: 先验概率分布和条件概率分布 '''
#设置样本特诊数目,数据集中手写图片为28*28,转换为向量是784维。
# (我们的数据集已经从图像转换成784维的形式了,CSV格式内就是)
featureNum = 784
#设置类别数目,0-9共十个类别
classNum = 10
#初始化先验概率分布存放数组,后续计算得到的P(Y = 0)放在Py[0]中,以此类推
#数据长度为10行1列
Py = np.zeros((classNum, 1))
#对每个类别进行一次循环,分别计算它们的先验概率分布
#计算公式为书中"4.2节 朴素贝叶斯法的参数估计 公式4.8"
for i in range(classNum):
#下方式子拆开分析
#np.mat(trainLabelArr) == i:将标签转换为矩阵形式,里面的每一位与i比较,若相等,该位变为Ture,反之False
#np.sum(np.mat(trainLabelArr) == i):计算上一步得到的矩阵中Ture的个数,进行求和(直观上就是找所有label中有多少个
#为i的标记,求得4.8式P(Y = Ck)中的分子)
#np.sum(np.mat(trainLabelArr) == i)) + 1:参考“4.2.3节 贝叶斯估计”,例如若数据集总不存在y=1的标记,也就是说
#手写数据集中没有1这张图,那么如果不加1,由于没有y=1,所以分子就会变成0,那么在最后求后验概率时这一项就变成了0,再
#和条件概率乘,结果同样为0,不允许存在这种情况,所以分子加1,分母加上K(K为标签可取的值数量,这里有10个数,取值为10)
#参考公式4.11
#(len(trainLabelArr) + 10):标签集的总长度+10.
#((np.sum(np.mat(trainLabelArr) == i)) + 1) / (len(trainLabelArr) + 10):最后求得的先验概率
Py[i] = ((np.sum(np.mat(trainLabelArr) == i)) + 1) / (len(trainLabelArr) + 10)
#转换为log对数形式
#log书中没有写到,但是实际中需要考虑到,原因是这样:
#最后求后验概率估计的时候,形式是各项的相乘(“4.1 朴素贝叶斯法的学习” 式4.7),这里存在两个问题:1.某一项为0时,结果为0.
#这个问题通过分子和分母加上一个相应的数可以排除,前面已经做好了处理。2.如果特诊特别多(例如在这里,需要连乘的项目有784个特征
#加一个先验概率分布一共795项相乘,所有数都是0-1之间,结果一定是一个很小的接近0的数。)理论上可以通过结果的大小值判断, 但在
#程序运行中很可能会向下溢出无法比较,因为值太小了。所以人为把值进行log处理。log在定义域内是一个递增函数,也就是说log(x)中,
#x越大,log也就越大,单调性和原数据保持一致。所以加上log对结果没有影响。此外连乘项通过log以后,可以变成各项累加,简化了计算。
#在似然函数中通常会使用log的方式进行处理(至于此书中为什么没涉及,我也不知道)
Py = np.log(Py)
#计算条件概率 Px_y=P(X=x|Y = y)
#计算条件概率分成了两个步骤,下方第一个大for循环用于累加,参考书中“4.2.3 贝叶斯估计 式4.10”,下方第一个大for循环内部是
#用于计算式4.10的分子,至于分子的+1以及分母的计算在下方第二个大For内
#初始化为全0矩阵,用于存放所有情况下的条件概率
Px_y = np.zeros((classNum, featureNum, 2))
#对标记集进行遍历
for i in range(len(trainLabelArr)):
#获取当前循环所使用的标记
label = trainLabelArr[i]
#获取当前要处理的样本
x = trainDataArr[i]
#对该样本的每一维特诊进行遍历
for j in range(featureNum):
#在矩阵中对应位置加1
#这里还没有计算条件概率,先把所有数累加,全加完以后,在后续步骤中再求对应的条件概率
Px_y[label][j][x[j]] += 1
#第二个大for,计算式4.10的分母,以及分子和分母之间的除法
#循环每一个标记(共10个)
for label in range(classNum):
#循环每一个标记对应的每一个特征
for j in range(featureNum):
#获取y=label,第j个特诊为0的个数
Px_y0 = Px_y[label][j][0]
#获取y=label,第j个特诊为1的个数
Px_y1 = Px_y[label][j][1]
#对式4.10的分子和分母进行相除,再除之前依据贝叶斯估计,分母需要加上2(为每个特征可取值个数)
#分别计算对于y= label,x第j个特征为0和1的条件概率分布
Px_y[label][j][0] = np.log((Px_y0 + 1) / (Px_y0 + Px_y1 + 2))
Px_y[label][j][1] = np.log((Px_y1 + 1) / (Px_y0 + Px_y1 + 2))
#返回先验概率分布和条件概率分布
return Py, Px_y
if __name__ == "__main__":
start = time.time()
# 获取训练集
print('start read transSet')
trainDataArr, trainLabelArr = loadData('../Mnist/mnist_train.csv')
# 获取测试集
print('start read testSet')
testDataArr, testLabelArr = loadData('../Mnist/mnist_test.csv')
#开始训练,学习先验概率分布和条件概率分布
print('start to train')
Py, Px_y = getAllProbability(trainDataArr, trainLabelArr)
#使用习得的先验概率分布和条件概率分布对测试集进行测试
print('start to test')
accuracy = model_test(Py, Px_y, testDataArr, testLabelArr)
#打印准确率
print('the accuracy is:', accuracy)
#打印时间
print('time span:', time.time() -start)





边栏推荐
- 分析框架——用户体验度量数据体系搭建
- Mapbox GL loading local publishing DEM data
- Redis是什么
- How to solve the problem of Caton screen when easycvr plays video?
- EasyCVR集群版本替换成老数据库造成的服务崩溃是什么原因?
- Maximum path and problem (cherry picking problem)
- [staff] pedal mark (step on pedal ped mark | release pedal * mark | corresponding pedal command in MIDI | continuous control signal | switch control signal)
- Streaming media cluster application and configuration: how to deploy multiple easycvr on one server?
- Depth first search to realize the problem of catching cattle
- GUI Graphical user interface programming example - color selection box
猜你喜欢

【火灾检测】基于matlab GUI森林火灾检测系统(带面板)【含Matlab源码 1921期】

Browser cache library design summary (localstorage/indexeddb)

免疫组化和免疫组学之间的区别是啥?

【leetcode】17. Letter combination of telephone number
![[Gym 102423]-Elven Efficiency | 思维](/img/cf/b65f3db1580a83478f8351cea22040.png)
[Gym 102423]-Elven Efficiency | 思维
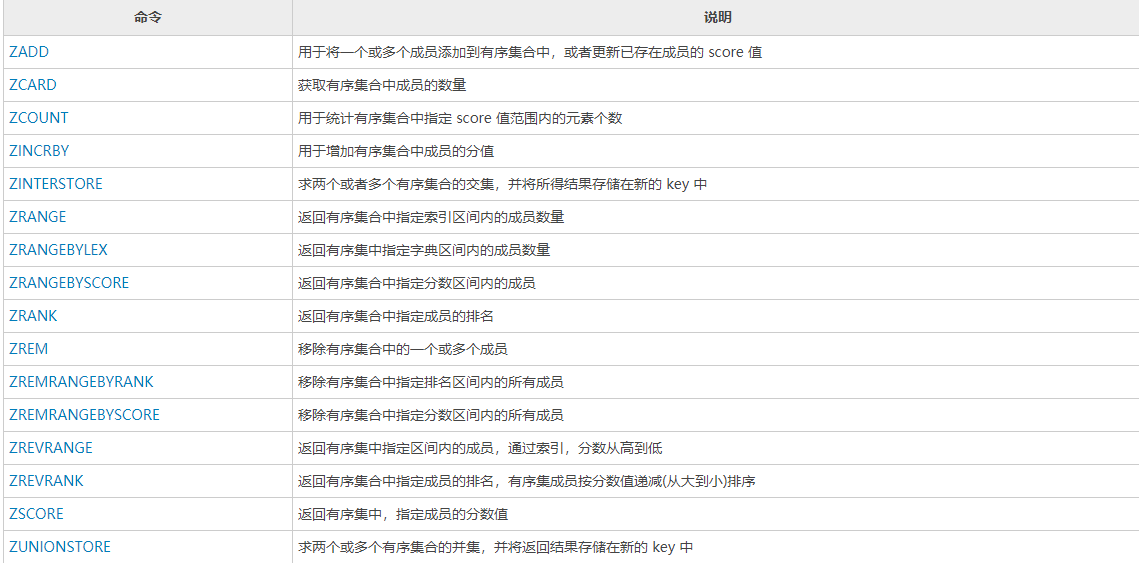
Redis common command manual
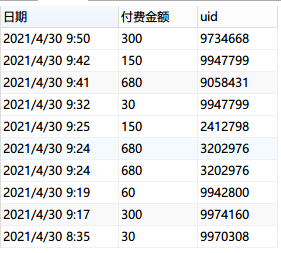
What is contemporaneous group analysis? Teach you to use SQL to handle

Precautions for installation and use of rotary joint

What is the difference between the history and Western blotting
674. longest continuous increasing sequence
随机推荐
What is the reason why easycvr can't watch the device video when it is connected to the home protocol?
基于.NetCore开发博客项目 StarBlog - (13) 加入友情链接功能
Baidu online disk login verification prompt: unable to access this page, or the QR code display fails, the pop-up window shows: unable to access this page, ensure the web address....
What is redis
Count the number of different palindrome subsequences in the string
如何进行数据库选型
Seven mistakes in IT Governance and how to avoid them
狼人杀休闲游戏微信小程序模板源码/微信小游戏源码
肖特基二极管在防止电源反接的作用
最新版CorelDRAW Technical Suite2022
滑环电机是如何工作的
Two fresh students: one is practical and likes to work overtime, and the other is skilled. How to choose??
Report on the convenient bee Lantern Festival: the first peak sales of pasta products this year; prefabricated wine dumplings became the winners
多维分析预汇总应该怎样做才管用?
Depth first search to realize the problem of catching cattle
Uvm:field automation mechanism
【leetcode】17. Letter combination of telephone number
Mapbox GL loading local publishing DEM data
第七天 脚本与特效
Pytorch -- use and modification of existing network model