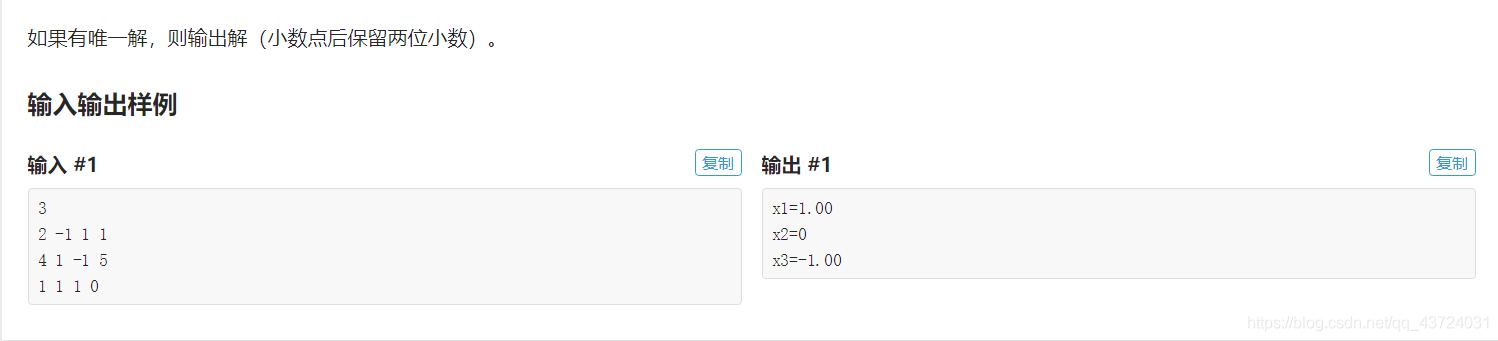
当前位置:网站首页>高斯消元
高斯消元
2022-07-26 09:29:00 【逃夭丶】
1.高斯消元法
高斯消元是求解线性方程组的一种算法,它可以用来求解矩阵的秩,以及求可逆矩阵的逆矩阵。它通过消除未知数来将原始线性系统转化为另一个简单的等价线性系统(详情见线性代数)。它的实质就是通过矩阵的初等行变化,将线性方程组的增广矩阵转化为行阶梯矩阵。
以下面的方程组为例,它的步骤为:
{ 2 x + y + z = 1 6 x + 2 y + z = − 1 − 2 x + 2 y + z = 7 \begin{cases} 2x + y + z = 1\\ 6x + 2y + z = -1\\ -2x + 2y + z = 7 \end{cases} ⎩⎪⎨⎪⎧2x+y+z=16x+2y+z=−1−2x+2y+z=7
1)构建增广矩阵(A,b),即系数矩阵A加上常数向量b
2)通过初等行变化,将矩阵变为更简单的三角式
3)得到方程的基础解系:
{ 2 x + y + z = 1 y + 2 z = 4 z = 1 \begin{cases} 2x + y + z = 1\\ y + 2z = 4\\ z = 1 \end{cases} ⎩⎪⎨⎪⎧2x+y+z=1y+2z=4z=1
4)回代方程得到解:
{ x = − 1 y = 2 z = 1 \begin{cases} x = -1\\ y = 2\\ z = 1 \end{cases} ⎩⎪⎨⎪⎧x=−1y=2z=1
2. 高斯·若尔当消元:
相对于高斯消元法,高斯·若尔当消元法最后的得到线性方程组更容易求解,它得到的是简化行列式。
const double eps = 1e-7;
int n;
double a[maxn][maxn],ans[maxn];
bool gauss(){
double del;
for(int i=1;i<=n;i++){
int k=i;
for(int j=i+1;j<=n;j++){
if(fabs(a[j][i])>fabs(a[k][i]))
k=j;
}
if(fabs(del=a[k][i])<eps) return false;
if(i!=k){
for(int j=i;j<=n+1;j++)
swap(a[i][j],a[k][j]);
}
for(int j=i;j<=n+1;j++) a[i][j]/=del;
for(k=1;k<=n;k++){
if(k!=i){
del=a[k][i];
for(int j=i;j<=n+1;j++)
a[k][j] -= a[i][j]*del;
}
}
}
return true;
}
模板题目:
P3389 【模板】高斯消元法
#include<cstdio>
#include<iostream>
#include<string>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<vector>
#include<map>
#include<queue>
#include<utility>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
const int maxn = 110;
const int inf = 0x3f3f3f3f3f;
const double eps = 1e-7;
int n;
double a[maxn][maxn];
bool gauss(){
double del;
for(int i=1;i<=n;i++){
int k=i;
for(int j=i+1;j<=n;j++){
if(fabs(a[j][i])>fabs(a[k][i]))
k=j;
}
if(fabs(del=a[k][i])<eps) return false;
if(i!=k){
for(int j=i;j<=n+1;j++)
swap(a[i][j],a[k][j]);
}
for(int j=i;j<=n+1;j++) a[i][j]/=del;
for(k=1;k<=n;k++){
if(k!=i){
del=a[k][i];
for(int j=i;j<=n+1;j++)
a[k][j] -= a[i][j]*del;
}
}
}
return true;
}
int main(void)
{
scanf("%d",&n);
for(int i=1;i<=n;i++){
for(int j=1;j<=n+1;j++){
scanf("%lf",&a[i][j]);
}
}
if(gauss()){
for(int i=1;i<=n;i++){
printf("%.2f\n",a[i][n+1]/a[i][i]);
}
}
else printf("No Solution\n");
return 0;
}
然后,既然是解方程组的话,就有三种情况,有唯一解,有无穷解,和无解。
那么用高斯·若尔当消元法如何判断这三种情况呢。
首先我们从线性代数知道,这个线性方程组的解和矩阵的秩有关。
例如:Ax = b,其中A是一个 n × m 的矩阵
若 R(A) = R(A,b) < n 有无穷解
若 R(A) = R(A,b) = n 有唯一解
若 R(A) < R(A,b) 无解
其实就是在消元后,找寻矩阵A和矩阵(A,b)的元素全为零的行的数目的关系。
int k1,k2;
void check(){
for(int i=1,j;i<=n;++i){
for(j=1;fabs(a[i][j])<eps&&j<=n+1;++j);
if(j>n+1) k2 = 1; //如果所在行,矩阵A和(A,b)都是零行,线性方程组可能有无穷解
if(j==n+1) k1 = 1; //如果所在行,矩阵A是零行,而矩阵(A,b)不是,那么一定无解
}
}
所以我们先看 k1,再看k2,最后输出唯一解。
check();
if(k1){
printf("-1");return ;}
if(k2){
printf("0");return ;}
for(int i=1;i<=n;i++){
printf("x%d=%.2f\n",i,a[i][n+1]/a[i][i]);
}
#include<cstdio>
#include<iostream>
#include<string>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<vector>
#include<map>
#include<queue>
#include<utility>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
const int maxn = 110;
const int inf = 0x3f3f3f3f3f;
const double eps = 1e-7;
int n;
double a[maxn][maxn];
int k1,k2;
void check(){
for(int i=1,j;i<=n;++i){
for(j=1;fabs(a[i][j])<eps&&j<=n+1;++j);
if(j>n+1) k2=1;
if(j==n+1) k1=1;
}
}
void gauss(){
double del;
for(int i=1;i<=n;i++){
int k=i;
for(int j=i+1;j<=n;j++){
if(fabs(a[j][i])>fabs(a[k][i]))
k=j;
}
if(fabs(del=a[k][i])<eps)
continue;
if(i!=k){
for(int j=i;j<=n+1;j++)
swap(a[i][j],a[k][j]);
}
for(int j=i;j<=n+1;j++) a[i][j]/=del;
for(k=1;k<=n;k++){
if(k!=i){
del=a[k][i];
for(int j=i;j<=n+1;j++)
a[k][j] -= a[i][j]*del;
}
}
}
check();
if(k1){
printf("-1");return ;}
if(k2){
printf("0");return ;}
for(int i=1;i<=n;i++){
printf("x%d=%.2f\n",i,a[i][n+1]/a[i][i]);
}
}
int main(void)
{
scanf("%d",&n);
for(int i=1;i<=n;i++){
for(int j=1;j<=n+1;j++){
scanf("%lf",&a[i][j]);
}
}
gauss();
return 0;
}
例题二:883. 高斯消元解线性方程组
#include<cstdio>
#include<iostream>
#include<string>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<vector>
#include<map>
#include<queue>
#include<utility>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
const int maxn = 110;
const int inf = 0x3f3f3f3f3f;
const double eps = 1e-7;
int n;
double a[maxn][maxn];
int k1,k2;
void check(){
for(int i=1,j;i<=n;++i){
for(j=1;fabs(a[i][j])<eps&&j<=n+1;++j);
if(j>n+1) k2 = 1;
if(j==n+1) k1 = 1;
}
}
void gauss(){
double del;
for(int i=1;i<=n;i++){
int k=i;
for(int j=i+1;j<=n;j++){
if(fabs(a[j][i])>fabs(a[k][i]))
k=j;
}
if(fabs(del=a[k][i])<eps)
continue;
if(i!=k){
for(int j=i;j<=n+1;j++)
swap(a[i][j],a[k][j]);
}
for(int j=i;j<=n+1;j++) a[i][j]/=del;
for(k=1;k<=n;k++){
if(k!=i){
del=a[k][i];
for(int j=i;j<=n+1;j++)
a[k][j] -= a[i][j]*del;
}
}
}
check();
if(k1){
printf("No solution");return ;}
if(k2){
printf("Infinite group solutions");return ;}
for(int i=1;i<=n;i++){
printf("%.2f\n",i,a[i][n+1]/a[i][i]);
}
}
int main(void)
{
scanf("%d",&n);
for(int i=1;i<=n;i++){
for(int j=1;j<=n+1;j++){
scanf("%lf",&a[i][j]);
}
}
gauss();
return 0;
}
边栏推荐
猜你喜欢
随机推荐
The difference between thread join and object wait
C# 托管与非托管
2020-12-29
服务器、客户端双认证(2)
IIS网站配置
Zxing simplified version, reprinted
Table extraction for opencv table recognition (2)
吴恩达机器学习之线性回归
Audio and video knowledge
I'm faded
php执行shell脚本
安卓 实现缓存机制,多种数据类型缓存
asp.net 使用redis缓存(二)
Force button list question
What is asynchronous operation
简单行人重识别代码到88%准确率 郑哲东 准备工作
Exception handling mechanism II
Fiddler抓包工具之移动端抓包
I'm faded
Byte buffer stream & character stream explanation