Chapter 3 stack, queue and array

Chapter one The introduction

Chapter two The linear table

The third chapter Stack 、 Queues and arrays

Chapter four strand

The fifth chapter Trees and binary trees

Chapter six chart

Chapter vii. lookup

Chapter viii. Sort

03 Stack 、 Queues and arrays

3.1 Definition of stack

Stack （stack） It is a linear table that only allows insertion or deletion at one end （LIFO）

Important terms ： To the top of the stack 、 At the bottom of the stack 、 Empty stack

3.2 The basic operation of the stack

InitStack(&S)： Initialization stack . Construct an empty stack S, Allocate memory space

DestroyStack(&S)： Destroy the stack . Destroy and release the stack S Memory space occupied

Push(&S, x)： Into the stack . Ruozhan S under , Will x Add to make it the top of the new stack

Pop(&S, &x)： Out of the stack . Ruozhan S Non empty , Then pop up the top element of the stack , And use x return

GetTop(S, &x)： Read top of stack elements . Ruozhan S Non empty , Then use x Back to top of stack element

StackEmpty(S)： Judge a stack S Is it empty . If it is empty , Then return to true, Otherwise return to false

3.3 Implementation of sequential stack

• Definition of sequential stack

  #define MaxSize 10 //  Define the maximum number of elements in the stack 
  typedef struct {
        
      ElemType data[MaxSize];	//  Static arrays hold the elements in the stack 
      int top;				///  Top pointer of stack 
  } SqStack;
  
  int main()
  {
        
      SqStack S;	//  Declare a sequential stack 
      ……
  }
  

• Stack in operation

  #define MaxSize 10 //  Define the maximum number of elements in the stack 
  typedef struct {
        
      ElemType data[MaxSize];	//  Static arrays hold the elements in the stack 
      int top;				///  Top pointer of stack 
  } SqStack;
  
  //  Put new elements on the stack 
  bool Push(SqStack &S, ElemType x) {
        
      if (S.top == MaxSize() - 1) return false;
      
      S.top = S.top + 1;
      S.data[S.top] = x;
      
      return true;
  }
  

• The stack,

  #define MaxSize 10 //  Define the maximum number of elements in the stack 
  typedef struct {
        
      ElemType data[MaxSize];	//  Static arrays hold the elements in the stack 
      int top;				///  Top pointer of stack 
  } SqStack;
  
  //  The stack, 
  bool Pop(SqStack &S, ElemType &x) {
        
      if (S.top == -1) return false;
      
      x = S.data[S.top];
      S.top = S.top - 1;
      
      return true;
  }
  

• Shared stack

  Using shared stack can improve the utilization of space

  #define MaxSize 10 //  Define the maximum number of elements in the stack 
  typedef struct {
        
      ElemType data[MaxSize];	//  Static arrays hold the elements in the stack 
      int top0;				// 0 No. stack top pointer 
      int top1;				// 1 No. stack top pointer 
  } SqStack;
  
  //  Initialization stack 
  void InitStack(ShStack &S) {
        
      S.top0 = -1;
      S.top1 = MaxSize();
  }
  

3.4 The realization of chain stack

A single linked list that can only be inserted and deleted at the head node can be regarded as a chain stack

• Definition

  typedef struct Linknode {
        
      ElemType data;
      struct Linknode *next;
  } *LiStack;
  

3.5 Definition of queue

queue （Queue） Is only allowed to insert at one end , Linear table deleted at the other end （FIFO）

Important terms ： Team head 、 A party 、 Empty queue

3.5 Basic operations of queues

InitQueue(&Q)： Initialize queue . Construct an empty queue

DestroyQueue(&Q)： Destroy queue . Destroy and release the queue Q Memory space occupied

EnQueue(&Q, x)： The team . If queue Q under , take x Join in , Make it a new tail

DeQueue(&Q, &x)： Out of the team . If queue Q Non empty , Delete team leader element , And use x return

GetHead(Q, &x)： Read the team leader element . If queue Q Non empty , Then assign the team head element to x

QueueEmpty(Q)： Determines if the queue is empty . Empty return true, Otherwise return to false

3.6 Sequential implementation of queues

Definition 、 initialization 、 Sentenced to empty 、 The team 、 Out of the team

#define MaxSize 10
typedef struct {
    
    ElemType data[MaxSize];
    int front, rear;
} SqQueue;

//  Initialize queue 
void InitQueue(SqQueue &Q) {
    
    Q.rear = Q.front = 0;
}

//  Determines if the queue is empty 
bool QueueEmpty(SqQueue Q) {
    
    if (Q.rear == Q.front) return true;
    else return false;
}

//  The team 
bool EnQueue(SqQueue &Q, ElemType x) {
    
    //  A space is sacrificed here to judge whether the team is full / Team space 
    if ((Q.rear + 1) % MaxSize == Q.front) return false;
    
    Q.data[Q.rear] = x;
    Q.rear = (Q.rear + 1) % MaxSize;
    
    return false;
}

//  Out of the team （ Delete a team head element , And use x return ）
bool DeQueue(SqQueue &Q, ElemType &x) {
    
    if (Q.rear == Q.front) return false;
    
    x = Q.data[Q.front];
    Q.front = (Q.front + 1) % MaxSize;
    
    return true;
}

//  Get the value of the team head element , use x return 
bool GetHead(SqQueue Q, ElemType &x) {
    
    if (Q.rear == Q.front)	return false;
    
    x = Q.data[Q.front];
    
    return true;
}

int main()
{
    
    SqQueue Q;
    
    ……
}

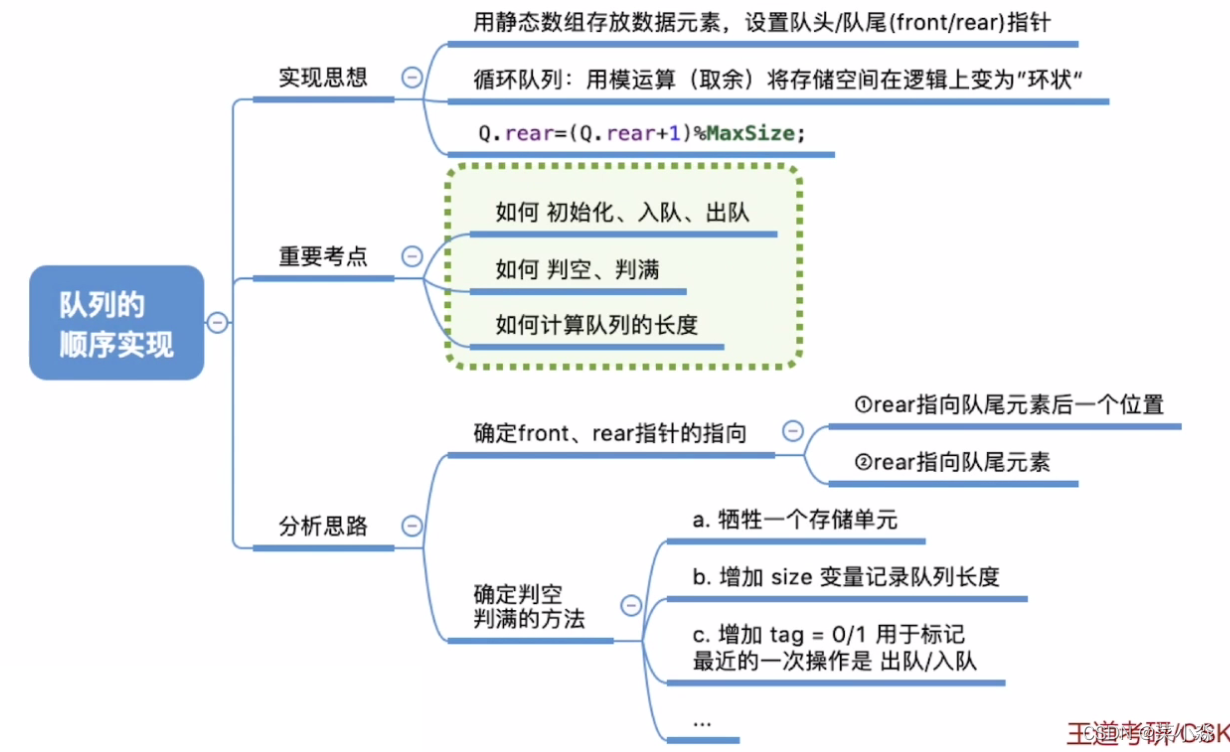
Determine whether a queue is empty / Three methods of full

• Sacrifice a space , Judge by taking mold
• Add a size attribute , Used to record the elements in the queue
• Add a tag, Used to store 0 and 1. Every time the delete operation succeeds , Du Ling tag=0; Every time the insert operation succeeds , Du Ling tag=1. Only delete , Can lead to the team empty , Only insert operation , Can lead to a full team .

3.7 Chained implementation of queues

typedef struct LinkNode {
    
    ElemType data;
    struct LinkNode *next;
} LinkNode;

tyepdef struct {
    
    LinkNode *front, *rear;
} LinkQueue;

//  Initialize queue （ Leading node ）
void InitQueue(LinkQueue &Q) {
    
    Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));
    Q.front -> next = null;
}

//  Initialize queue （ No leading node ）
void InitQueue(LinkQueue &Q) {
    
    Q.front = null;
    Q.rear = null;
}

//  Determines if the queue is empty （ Leading node ）
bool IsEmpyt(LinkQueue Q) {
    
    if (Q.front == Q.rear) return true;
    else return false;
}

//  Determines if the queue is empty （ No leading node ）
bool IsEmpyt(LinkQueue Q) {
    
    if (Q.front == null) return true;
    else return false;
}

//  New elements in the team （ Leading node ）
void EnQueue(LinkQueue &Q, ElemType x) {
    
    LinkNode *s = (LinkNode *) malloc(sizeof(LinkNode));
    
    s -> data = x;
    s -> next = null;
    Q.rear -> next = s;
    Q.rear = s;
}

//  New elements in the team （ No leading node ）
void EnQueue(LinkQueue &Q, ElemType x) {
    
    LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));
    
    s -> data = x;
    s -> next = null;
    if (Q.front == null) {
    
        Q.front = s;
        Q.rear = s;
    } else {
    
        Q.rear -> next = s;
        Q.rear = s;
    }
}

//  Team leader element out of the team （ Leading node ）
bool DeQueue(LinkQueue &Q, ElemType &x) {
    
    if (Q.front == Q.rear) return false;	//  Air force 
    
    LinkNode *p = Q.front -> next;
    x = p -> data;	//  With variable x Return to team leader element 
    Q.front -> next = p -> next;	//  Modify the header node next The pointer 
    if (Q.rear == p)	//  This is the last node out of the team 
        Q.rear = Q.front;	//  modify rear The pointer 
    free(p);	//  Release node space 
    
    return true;
}

//  Team leader element out of the team （ No leading node ）
bool DeQueue(LinkQueue &Q, ElemType &x) {
    
    if (Q.front == null) return false;	//  Air force 
    
    LinkNode *p = Q.front;	// p Point to the node out of the team 
    x = p -> data;	//  With variable x Return to team leader element 
    Q.front = p -> next;	//  modify front The pointer 
    if (Q.rear == p) {
    	//  This is the last node out of the team 
        Q.front = null;
        Q.rear = null;
    }
    free(p);	//  Release node space 
    
    return true;
}

void testLinkQueue() {
    
    LinkQueue Q;
    InitQueue(Q);
    
    ……
}

3.8 deque

deque ： It is only allowed to insert... From both ends 、 Linear table deleted at both ends

Input restricted double ended queue ： It is only allowed to insert... From one end 、 Linear table deleted at both ends

Output the first double ended queue ： It is only allowed to insert... From both ends 、 Delete one end of the linear table

3.9 The application of the stack —— Parentheses matching

The last left parenthesis is matched first （LIFO）

Each occurrence of a right parenthesis consumes an left parenthesis （ Out of the stack )

Put it on the stack when you encounter the left bracket , If you encounter the right parenthesis, you will get out of the stack

#define MaxSize 10
typedef struct {
    
    char data[MaxSize];
    int top;
} SqStack;

//  Initialization stack 
void InitStack(SqStack &S) {
    }

//  Judge whether the stack is empty 
bool StackEmpty(SqStack S) {
    }

//  Put new elements on the stack 
bool Push(SqStack &S, char x) {
    }

//  Stack top element out of stack , use x return 
bool Pop(SqStack &S, char &x) {
    }

bool bracketCheck(char str[], int length) {
    
    SqStack S;
    InitStack(S);
    for (int i = 0; i < length; i ++) {
    
        if (str[i] == '(' || str[i] == '[' || str[i] == '{') {
    
            Push(S, str[i]);
        } else {
    
            if (StackEmpty(S))
                return false;
            
            char topElem;
            Pop(S, topElem);
            if (str[i] == ')' && topElem != '(') return false;
            else if (str[i] == ']' && topElem != '[') return false;
            else if (str[i] == '}' && topElem != '{') return false;
        }
    }
    
    return StackEmpty(S);
}

3. 10 The application of the stack —— Arithmetic expression

• Prefix expression ： Operator before two operands

• Infix expression ： Operator is in the middle of two operands

• Postfix expression ： Operator after two operands

  computing method ： Scanning from left to right , Every operator encountered , Let the last two operands in front of the operator perform the corresponding operation , The combination is an operand

3.11 The application of stack in recursion

Features of function calls ： The last called function is executed first and ends （LIFO）

When a function is called , You need to use a stack to store ：

• Call return address
• Actual parameters
• local variable

When called recursively , The function call stack can be called “ Recursive work stack ”

Every time you enter a layer of recursion , Press the information required for recursive calls into the top of the stack ;

Every exit layer recursion , The corresponding message pops up from the top of the stack

3.12 Application of queues

Sequence traversal of trees

Breadth first traversal of graphs

The first come, first serve strategy of the operating system （FCFS）

3.13 Compressed storage of special matrices

• Compressed storage of symmetric matrix

  if n Any element of a square matrix of order a_i,j There are a_i,j=a_j,i, Then the matrix is called a symmetric matrix

  Ordinary storage ：n*n Two dimensional array

  Compressed storage policy ： Store only the main diagonal + Lower triangle （ Or the main diagonal + Upper triangle ）

  Store each element into a one-dimensional array according to the principle of row priority

  How to use ？

  It can realize a from matrix subscript to one-dimensional array subscript ” mapping “ function
  

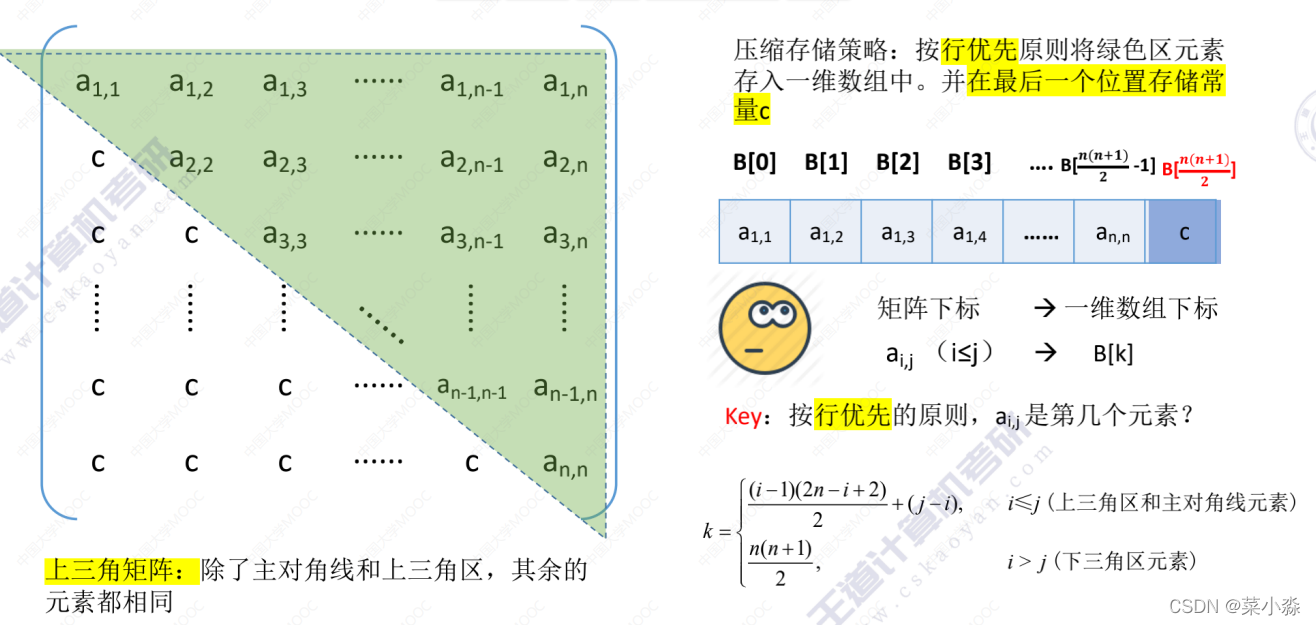
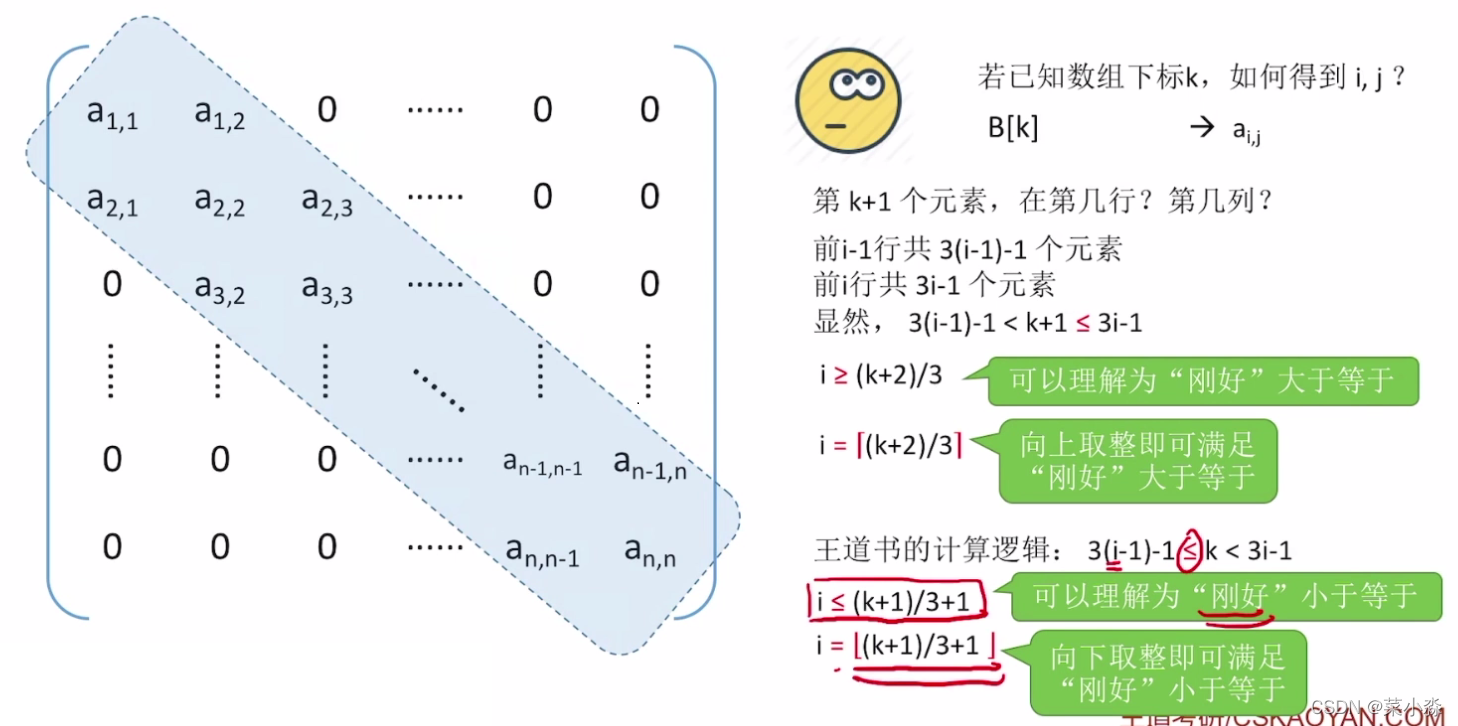
• Compressed storage of triangular matrix

• Compressed storage of sparse matrix