当前位置:网站首页>Derivation of Euler angle differential equation
Derivation of Euler angle differential equation
2022-07-29 02:19:00 【Mubai 001】
Preface
I recently studied at dark blue College 《 Vision slam Advanced : Handwriting from scratch VIO》, The second chapter talks about IMU sensor , The Euler angle form of rotation integral is mentioned , Just recently, this formula has also been used , Therefore, the detailed derivation process of the formula is carefully deduced .
Some instructions
According to custom , The navigation coordinate system used in the derivation process is the northeast sky coordinate system (ENUENUENU),IMU The coordinate system of the carrier is : Right 、 front , On (XXX, YYY, ZZZ), The rotation order of Euler angle is :ZZZ, XXX, YYY ( Yaw 、 pitch , roll ). We can see from the following derivation later , The derivation formula based on Euler angle method is related to the definition of carrier coordinate system and rotation order , So here we make some explanations . In addition, it can be used matlab Auxiliary formula derivation , Very convenient , It's not easy to make mistakes. .
Derivation process
Rbn=Rb1(y)⋅R12(p)⋅R2n(r)R_{n}^{b}=R_{1}^{b}(y) \cdot R_{2}^{1}(p) \cdot R_{n}^{2}(r)Rnb=R1b(y)⋅R21(p)⋅Rn2(r)
among :
Rb1(y)=⎡⎣cysy0−sycy0001⎤⎦R_{1}^{b}(y)=\left[\begin{array}{ccc}{c y} & {-s y} & {0} \\{s y} & {c y} & {0} \\{0} & {0} & {1}\end{array}\right]R1b(y)=⎣⎡cysy0−sycy0001⎦⎤
R12(p)=⎡⎣1000cpsp0−spcp⎤⎦R_{2}^{1}(p)=\left[\begin{array}{ccc}{1} & {0} & {0} \\{0} & {c p} & {-s p} \\{0} & {s p} & {c p}\end{array}\right]R21(p)=⎣⎡1000cpsp0−spcp⎦⎤
R2n(r)=⎡⎣cr0−sr010sr0cr⎤⎦R_{n}^{2}(r)=\left[\begin{array}{ccc}{c r} & {0} & {s r} \\{0} & {1} & {0} \\{-s r} & {0} & {c r}\end{array}\right]Rn2(r)=⎣⎡cr0−sr010sr0cr⎦⎤
Rb1(y)R_{1}^{b}(y)R1b(y) It means around ZZZ The rotation matrix of the axis ,R12(p)R_{2}^{1}(p)R21(p) It means around XXX The rotation matrix of the axis , R2n(r)R_{n}^{2}(r)Rn2(r) It means around YYY The rotation matrix of the axis . RbnR_{n}^{b}Rnb It is the conversion matrix from the navigation system to the carrier coordinate system , XbX^{b}Xb Represents the coordinates under the carrier coordinate system , XnX^{n}Xn Represents the coordinates in the navigation coordinate system , Then there is the following formula :
Xn=Rbn⋅XbX^{n}=R_{n}^{b} \cdot X^{b}Xn=Rnb⋅Xb
XbX^{b}Xb The solution is as follows :
Xb=Rn2(r)⋅R21(p)⋅R1b(y)⋅XnX^{b}=R_{2}^{n}(r) \cdot R_{1}^{2}(p) \cdot R_{b}^{1}(y) \cdot X^{n}Xb=R2n(r)⋅R12(p)⋅Rb1(y)⋅Xn
First step :
Suppose you have completed the rotation around three axes , Then finally around YYY The angular velocity of the axis is the same in the carrier coordinate system and the navigation coordinate system , So there is the following formula :
ωb(r)=⎡⎣⎢0drdt0⎤⎦⎥\omega_{b}(r)=\left[\begin{array}{c}{0} \\{\frac{d r}{d t}} \\{0}\end{array}\right]ωb(r)=⎣⎡0dtdr0⎦⎤
The second step :
Suppose the first two sets of rotations have been completed , The last set of rotations is not complete , If you then complete the last step of rotation , Is the same as the first step , Around the XXX The angular velocity of the axis is the same in the two coordinate systems , Then there is the following formula :
ωb(p)=Rn2(r)⋅⎡⎣⎢dpdt00⎤⎦⎥\omega_{b}(p)=R_{2}^{n}(r) \cdot\left[\begin{array}{c}{\frac{d p}{d t}} \\{0} \\{0}\end{array}\right]ωb(p)=R2n(r)⋅⎣⎡dtdp00⎦⎤
The third step :
The analysis is similar to the second step . Suppose you have completed the first set of rotations , The last two sets of rotations were not completed , If you then complete the last two sets of rotations , Then around ZZZ The angular velocity of the axis is the same in the two coordinate systems , Then there is the following formula :
ωb(y)=Rn2(r)⋅R21(p)⋅⎡⎣⎢00dydt⎤⎦⎥\omega_{b}(y)=R_{2}^{n}(r) \cdot R_{1}^{2}(p) \cdot\left[\begin{array}{c}{0} \\{0} \\{\frac{d y}{d t}}\end{array}\right]ωb(y)=R2n(r)⋅R12(p)⋅⎣⎡00dtdy⎦⎤
In the end :
ωb=ωb(y)+ωb(p)+ωb(r)\omega_{b}=\omega_{b}(y)+\omega_{b}(p)+\omega_{b}(r)ωb=ωb(y)+ωb(p)+ωb(r)
ωb=Rn2(r)⋅R21(p)⋅⎡⎣⎢00dydt⎤⎦⎥+Rn2(r)⋅⎡⎣⎢dpdt00⎤⎦⎥+⎡⎣⎢0drdt0⎤⎦⎥=⎡⎣cr0sr010−sr⋅cpspcr⋅cp⎤⎦⋅⎡⎣⎢⎢dpdtdrdtdydt⎤⎦⎥⎥\omega_{b}=R_{2}^{n}(r) \cdot R_{1}^{2}(p) \cdot\left[\begin{array}{c}{0} \\{0} \\{\frac{d y}{d t}}\end{array}\right]+R_{2}^{n}(r) \cdot\left[\begin{array}{c}{\frac{d p}{d t}} \\{0} \\{0}\end{array}\right]+\left[\begin{array}{c}{0} \\{\frac{d r}{d t}} \\{0}\end{array}\right]=\left[\begin{array}{ccc}{c r} & {0} & {-s r \cdot c p} \\{0} & {1} & {s p} \\{s r} & {0} & {c r \cdot c p}\end{array}\right] \cdot\left[\begin{array}{c}{\frac{d p}{d t}} \\{\frac{d r}{d t}} \\{\frac{d y}{d t}}\end{array}\right]ωb=R2n(r)⋅R12(p)⋅⎣⎡00dtdy⎦⎤+R2n(r)⋅⎣⎡dtdp00⎦⎤+⎣⎡0dtdr0⎦⎤=⎣⎡cr0sr010−sr⋅cpspcr⋅cp⎦⎤⋅⎣⎡dtdpdtdrdtdy⎦⎤
In the above formula ωb\omega_{b}ωb Is the projection of angular velocity in the carrier coordinate system , Gyroscope data ,dpdt\frac{d p}{d t}dtdp,drdt\frac{d r}{d t}dtdr,dydt\frac{d y}{d t}dtdy Is the projection of angular velocity in the navigation coordinate system .
The same can be :
⎡⎣⎢⎢dpdtdrdtdydt⎤⎦⎥⎥=⎡⎣crsp⋅sr/cp−sr/cp010sr−sp⋅cr/cpcr/cp⎤⎦⋅ωb\left[\begin{array}{l}{\frac{d p}{d t}} \\{\frac{d r}{d t}} \\{\frac{d y}{d t}}\end{array}\right]=\left[\begin{array}{ccc}{c r} & {0} & {s r} \\{s p \cdot \operatorname{sr} / c p} & {1} & {-s p \cdot c r / c p} \\{-s r / c p} & {0} & {c r / c p}\end{array}\right] \cdot \omega_{b}⎣⎡dtdpdtdrdtdy⎦⎤=⎣⎡crsp⋅sr/cp−sr/cp010sr−sp⋅cr/cpcr/cp⎦⎤⋅ωb
It can be seen from the above formula , When the pitch angle approaches 90∘90^{\circ}90∘ when , There is no solution , Therefore, Euler angle method cannot be used in full attitude aircraft , Equal to platform inertial navigation “ The ring frame is self-locking ”, Pay attention to this when using this formula .
Matlab The code of auxiliary derivation is as follows :
% Derivation of Euler angle formula for updating attitude matrix
% Rotation order :Z,X,Y
% Reference resources : KINEMATICS OF MOVING FRAMES MIT KINEMATICS OF MOVING FRAMES MIT
syms r p y
syms dpdt drdt dydt
x_p = [1, 0, 0;
0, cos(p), -sin(p);
0, sin(p), cos(p)];
y_r = [cos(r), 0, sin(r);
0, 1, 0;
-sin(r), 0, cos(r)];
z_y = [cos(y), -sin(y), 0;
sin(y), cos(y), 0;
0, 0, 1];
x_p_trans = x_p';
y_r_trans = y_r';
z_y_trans = z_y';
dp_t_vector=[dpdt;0;0]; %X Axis
dr_t_vector=[0;drdt;0]; %Y Axis
dy_t_vector=[0;0;dydt]; %Z Axis
% y_r_trans x_p_trans z_y_trans
% Gyroscope angular velocity
ang_vel=y_r_trans*x_p_trans*dy_t_vector+y_r_trans*dp_t_vector+dr_t_vector
% give the result as follows :
% ang_vel=
% dpdt*cos(r) - dydt*cos(p)*sin(r)
% drdt + dydt*sin(p)
% dpdt*sin(r) + dydt*cos(p)*cos(r)
% The results are as follows : % [dpdt;drdt;dydt]
% The transformation matrix is as follows :
% [cos(r), 0, -sin(r)*cos(p);
% 0, 1, sin(p);
% sin(r), 0, cos(r)*cos(p)]
% Transpose matrix
ang_vel_matrix= [cos(r), 0, -sin(r)*cos(p);
0, 1, sin(p);
sin(r), 0, cos(r)*cos(p)];
ang_vel_inv_matrix = inv(ang_vel_matrix)
% give the result as follows :
% ang_vel_inv_matrix =
%
% [ cos(r)/(cos(r)^2 + sin(r)^2), 0, sin(r)/(cos(r)^2 + sin(r)^2)]
% [ (sin(p)*sin(r))/(cos(p)*cos(r)^2 + cos(p)*sin(r)^2), 1, -(cos(r)*sin(p))/(cos(p)*cos(r)^2 + cos(p)*sin(r)^2)]
% [ -sin(r)/(cos(p)*cos(r)^2 + cos(p)*sin(r)^2), 0, cos(r)/(cos(p)*cos(r)^2 + cos(p)*sin(r)^2)]
% You can get :
% [ cos(r), 0, sin(r)]
% [ (sin(p)*sin(r))/cos(p), 1, -cos(r)*sin(p)/cos(p)]
% [ -sin(r)/cos(p), 0, cos(r)/cos(p)]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
At the same time, I also verified the reference 2 The derivation formula in , Reference resources 2 The rotation order in is ZZZ,YYY,XXX, Derivation results and 2 In the agreement . The code is as follows :
% Derivation of Euler angle formula for updating attitude matrix
% Rotation order :Z,Y,X
% Reference resources : KINEMATICS OF MOVING FRAMES MIT KINEMATICS OF MOVING FRAMES MIT
syms r p y
syms dpdt drdt dydt
x_r = [1, 0, 0;
0, cos(r), -sin(r);
0, sin(r), cos(r)];
y_p = [cos(p), 0, sin(p);
0, 1, 0;
-sin(p), 0, cos(p)];
z_y = [cos(y), -sin(y), 0;
sin(y), cos(y), 0;
0, 0, 1];
x_r_trans = x_r';
y_p_trans = y_p';
z_y_trans = z_y';
dr_t_vector = [drdt;0;0]; %x Axis
dp_t_vector = [0;dpdt;0]; %y Axis
dy_t_vector = [0;0;dydt]; %z Axis
% Rotation order :x_r_trans y_p_trans z_y_trans
% Gyroscope angular velocity
ang_vel = x_r_trans*y_p_trans*dy_t_vector+x_r_trans*dp_t_vector+dr_t_vector
% give the result as follows
% ang_vel =
% drdt - dydt*sin(p)
% dpdt*cos(r) + dydt*cos(p)*sin(r)
% dydt*cos(p)*cos(r) - dpdt*sin(r)
% drdt; dpdt; dydt
% Put it in order :
% 1 , 0 , -sin(p);
% 0 , cos(r) , sin(r)*cos(p);
% 0 , -sin(r) , cos(p)*cos(r);
% Transpose matrix
ang_vel_matrix=[1 , 0 , -sin(p);
0 , cos(r) , sin(r)*cos(p);
0 , -sin(r) , cos(r)*cos(p)];
ang_vel_inv_matrix = inv(ang_vel_matrix)
% give the result as follows :
% [ 1, (sin(p)*sin(r))/(cos(p)*cos(r)^2 + cos(p)*sin(r)^2), (cos(r)*sin(p))/(cos(p)*cos(r)^2 + cos(p)*sin(r)^2)]
% [ 0, cos(r)/(cos(r)^2 + sin(r)^2), -sin(r)/(cos(r)^2 + sin(r)^2)]
% [ 0, sin(r)/(cos(p)*cos(r)^2 + cos(p)*sin(r)^2), cos(r)/(cos(p)*cos(r)^2 + cos(p)*sin(r)^2)]
% Simplify to :
% [ 1, sin(r)*tan(p), cos(r)*tan(p)]
% [ 0, cos(r), -sin(r)]
% [ 0, sin(r)/cos(p), cos(r)/cos(p)]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
Reference resources
1.《 Basic principle of inertial navigation 》 Liu Baozhong
2. KINEMATICS OF MOVING FRAMES MIT
3. Deep Blue College 《 Vision slam Advanced : Handwriting from scratch VIO》 Course
边栏推荐
- Idea connection database
- Mysql存储json格式数据
- Leetcode/0 and 1 consecutive subarrays with the same number
- 特殊流&Properties属性集实例遇到的问题及解决方法
- “蔚来杯“2022牛客暑期多校训练营3,签到题CAJHF
- 多线程浅谈
- 【云原生与5G】微服务加持5G核心网
- 控制输入框弹出弹窗 和不弹出窗口
- JVM内存溢出在线分析Dump文件以及在线分析打开.hprof文件得出JVM运行报告jvisualvm怎么在线分析
- Verilog procedure assignment statements: blocking & non blocking
猜你喜欢
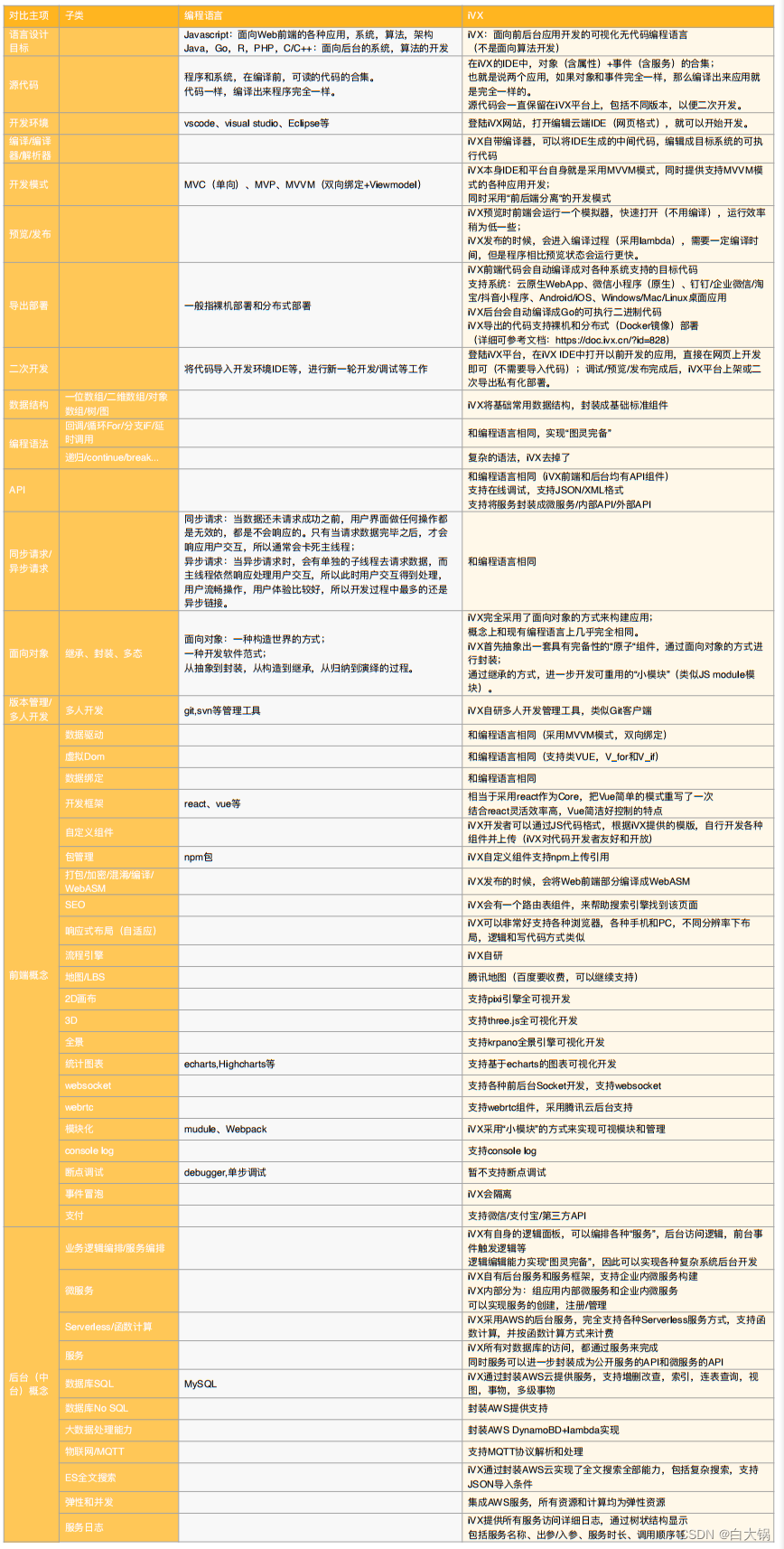
Detailed explanation of IVX low code platform series -- Overview (II)
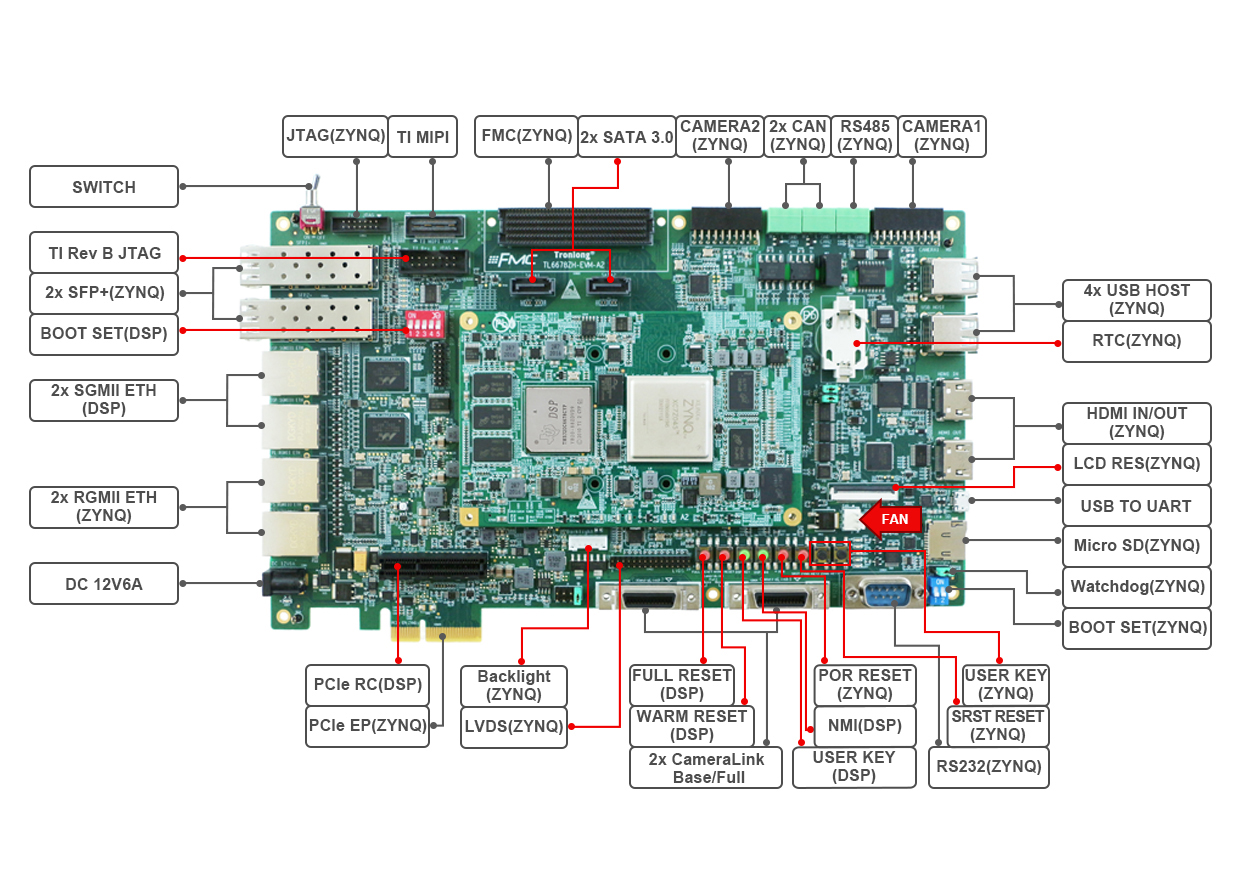
PS + PL heterogeneous multicore case development manual for Ti C6000 tms320c6678 DSP + zynq-7045 (2)
![[cloud native and 5g] micro services support 5g core network](/img/c9/4ccacd1e70285c2ceb50c324e5018c.png)
[cloud native and 5g] micro services support 5g core network

字符流综合练习解题过程

awvs无法启动问题

12. < tag dynamic programming and subsequence, subarray> lt.72. edit distance

实验二:Arduino的三色灯实验

Mathematical modeling -- bus scheduling optimization

Summarize in the middle of the year | talk to yourself, live in the present, and count every step

第十五天(VLAN相关知识)
随机推荐
[simple implementation and extension of one · data | array heap]
自定义mvc原理和框架实现
What is scope and scope chain
[RT learning note 1] RT thread peripheral routine - control LED light flashing
MotionLayout--在可视化编辑器中实现动画
Navigation -- realize data transmission and data sharing between fragments
Data query of MySQL (multi table query)
[circuit design] peak voltage and surge current
JetPack--Navigation实现页面跳转
特殊流&Properties属性集实例遇到的问题及解决方法
Leetcode/ and continuous shortest subarray greater than or equal to target
How to write, load and unload plug-ins in QT
控制输入框弹出弹窗 和不弹出窗口
Try to understand the essence of low code platform design from another angle
第十五天(VLAN相关知识)
Why can't Bi software do correlation analysis
Opencv image sharpness evaluation (camera autofocus)
Excel 打开包含汉字的 csv 文件出现乱码该怎么办?
Day 14: continued day 13 label related knowledge
ES6 语法扩展