当前位置:网站首页>二叉树——搜索树
二叉树——搜索树
2022-07-27 05:22:00 【只羡鸳鸯不羡仙仙】
目录
一、BST
1、BST的解释
(1)BST就是二分搜索树,是二叉树的一种
(2)每个树的左子树的所有节点值<根节点值<所有右子树的节点值
(3)一般来说二分搜索树中不存在重复节点
(4)存储的节点必须具备可以比较的能力(要么实现Comparable接口,要么传入比较器)
2、BST添加节点

public void add(int val){
root=add(root,val);
}
/**
* 向当前的root为根的BST中插入一个新元素,返回插入后的根
* @param root
* @param val
* @return
*/
private BSTnode add(BSTnode root, int val) {
if (root==null){
BSTnode node=new BSTnode(val);
size++;
return node;
}
if (val< root.val){
//此时新元素小于根节点,就应该添加到左子树
root.left=add(root.left,val);
}
if (val> root.val){
//此时新元素大于根节点,就用该添加到右子树
root.right=add(root.right,val);
}
return root;
}
3、在BST中查找val
不断递归的去和树的根相比
val==root.val就说明找到了
val<root,val就继续在左子树中找
val>root.val就继续在右子树中找
直到root==null就说明就根本不存在这个节点
public boolean contains(int val){
return contains(root,val);
}
/**
* 判断当前BST中是否包含val
* @param root
* @param val
* @return
*/
private boolean contains(BSTnode root, int val) {
if (root==null){
return false;
}
if (root.val==val){
return true;
}else if (val<root.val){
return contains(root.left,val);
}else {
return contains(root.right,val);
}
}4、按照先序遍历的方式打印当前的BST
@Override
public String toString() {
StringBuilder sb=new StringBuilder();
generateBSTString(root,0,sb);
return sb.toString();
}
/**
* 按照先序遍历
* @param root
* @param height
* @param sb
*/
private void generateBSTString(BSTnode root, int height, StringBuilder sb) {
if (root==null){
sb.append(generateHeightStr(height)).append("NULL\n");
return;
}
sb.append(generateHeightStr(height)).append(root.val).append("\n");
//递归打印左子树
generateBSTString(root.left,height+1,sb);
//递归打印右子树
generateBSTString(root.right,height+1,sb);
}
/**
* 按照高度打印--,表示节点在第几层
* @param height
* @return
*/
private String generateHeightStr(int height){
StringBuilder sb=new StringBuilder();
for (int i = 0; i <height; i++) {
sb.append("--");
}
return sb.toString();
}
5、在BST中找出最大值和最小值
根据BST可以发现,最大值就是先序遍历中第一个右子树为空的节点,最小值就是先序遍历中第一个左子树为空的节点
public int findmin(){
if (size==0){
throw new NoSuchElementException("BST is emty!Dont'have min!");
}
return min(root).val;
}
/**
* 一root为根的BST中找到最小值节点
* @param root
* @return
*/
private BSTnode min(BSTnode root) {
if (root.left==null){
//第一个左子树为空的节点
return root;
}
return min(root.left);
}
public int findmax(){
if (size==0){
throw new NoSuchElementException("BST is emty!Dont'have max!");
}
return max(root).val;
}
private BSTnode max(BSTnode root) {
if (root.right==null){
//第一个右子树为空的节点
return root;
}
return max(root.right);
}6、删除最大值和最小值
/**
* 删除BST中的最小值,返回最小节点值
* @return
*/
public int removeMin(){
if (size==0){
throw new NoSuchElementException("BST is emty!cannot remove!");
}
BSTnode minnode=min(root);
root=removemin(root);
return minnode.val;
}
/**
* 在root为根节点的BST中,删除最小值,返回根节点
* @param root
* @return
*/
private BSTnode removemin(BSTnode root) {
if(root.left==null){
//root就是待删除的节点
BSTnode right=root.right;
root.left=root.right=root=null;
size--;
return right;
}
root.left=removemin(root.left);
return root;
}
/**
* 删除BST的最大值,返回最大节点值
* @return
*/
public int removeMax(){
if (size==0){
throw new NoSuchElementException("BST is emty!cannot remove!");
}
BSTnode maxnode=max(root);
root=removemax(root);
return maxnode.val;
}
/**
* 一root为根节点的BST,删除最小值,返回根节点
* @param root
* @return
*/
private BSTnode removemax(BSTnode root) {
if (root.right==null){
//root就是待删除的点
BSTnode left=root.left;
root.left=root.right=root=null;
size--;
return left;
}
root.right=removemax(root.right);
return root;
}7、在BST中删除任意值val
删除任意值val可以分为以下两种情况


public void remove(int val){
if (size==0){
throw new NoSuchElementException("BST is emty!cannot remove!");
}
root=remove(root,val);
}
/**
* 在以root为根节点的BST中删除值为val的节点,返回根节点
* @param root
* @param val
* @return
*/
private BSTnode remove(BSTnode root, int val) {
if (root==null){
//该树中没有值为val的节点
throw new NoSuchElementException("BST has not val!");
}else if (val<root.val){
//此时就在左子树中删除val
root.left=remove(root.left,val);
return root;
} else if (val> root.val) {
//此时在右子树中删除val
root.right=remove(root.right,val);
return root;
}else{
//root,val==val
//root就是待删除的节点
if (root.left==null){
//此时就是类似于删除最小值
BSTnode right=root.right;
root.right=root=null;
size--;
return right;
}
if (root.right==null){
//此时就类似于删除最大值
BSTnode left=root.left;
root.left=root=null;
return left;
}
//此时待删除节点的左右子树都不为空,这里以右子树最小值为例
BSTnode successor=min(root.right);
//先在右子树中删除这个节点
successor.right=removemin(root.right);
//连接root.left
successor.left=root.left;
//顺便让删除的节点彻底清空
root.left=root.right=root=null;
return successor;
}
}删除后的结果

二、相关代码
边栏推荐
猜你喜欢

Unity engine starts to migrate from mono to.Net coreclr
哈夫曼树的求法,代码实现及证明,图文解释
![[Arduino] reborn Arduino monk (1)](/img/ce/67118ebd430a0ff3ef98ec8524ee4a.jpg)
[Arduino] reborn Arduino monk (1)

IP核之RAM

导航相关消息
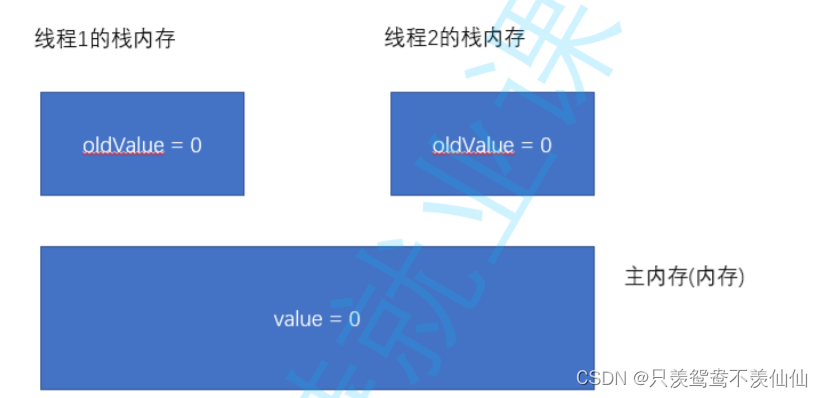
Multi threaded CAS, synchronized lock principle, JUC and deadlock

Remote sensing image recognition - making data sets
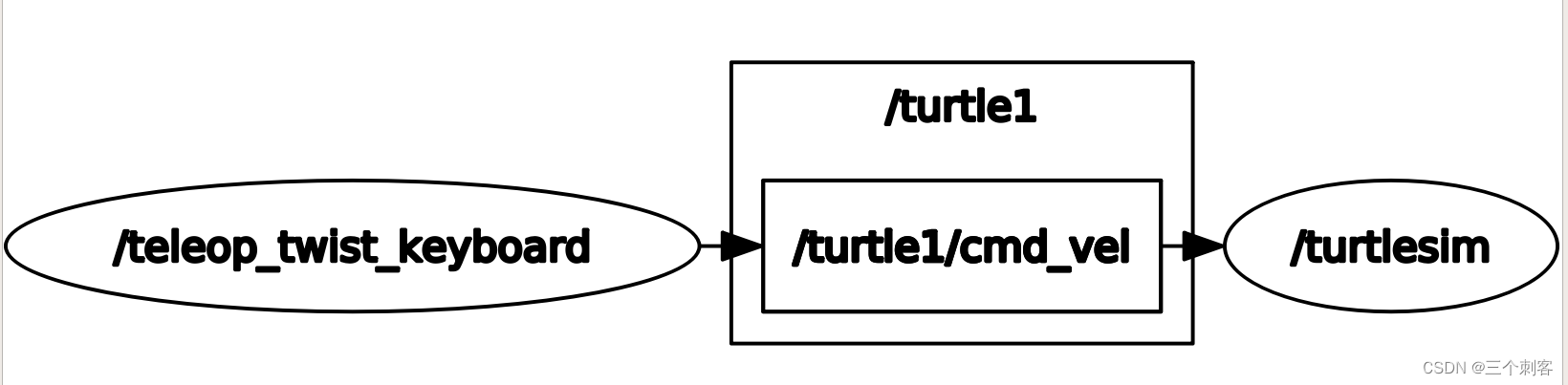
ROS topic name setting

性感素数(Acwing每日一题)

How to choose the correct server backup method
随机推荐
Multi threaded CAS, synchronized lock principle, JUC and deadlock
Thesis writing (harvest)
力扣 236. 二叉树的最近公共祖先
5g's past and present life -- a brief introduction to the development of mobile communication
Comparison of communication mechanisms
机器人导航实现
导航相关消息
Code implementation and introduction of all commonly used sorting
Dynamic programming for solving problems (2)
ROS topic name setting
Wireshark IP address domain name resolution
力扣每日一题leetcode 513. 找树左下角的值
Unable to start program, access denied?
Pzk's first understanding of pointer in learning C language
Man moon myth reading notes
Brief introduction to unity menu interface
SQL novice
Dynamic planning for solving problems (3)
学习软件测试时需要配备的运行环境需求搭建
Unity hub login no response
 https://gitee.com/ren-xiaoxiong/rocket_class_ds/tree/master/src/BST
https://gitee.com/ren-xiaoxiong/rocket_class_ds/tree/master/src/BST