当前位置:网站首页>golang刷leetcode动态规划(9)不同路径 II
golang刷leetcode动态规划(9)不同路径 II
2022-08-02 17:37:00 【用户9710217】
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
说明:m 和 n 的值均不超过 100。
示例 1:
输入:
[
[0,0,0],
[0,1,0],
[0,0,0]
]
输出: 2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右解题思路 1,这是一个典型的动态规划题
2,子问题拆分:由于每个点只能从左往右或者从上往下
递推公式为m[i][j]=m[i-1][j]+m[i][j-1],由于用到了i-1,j-1所以i,j均递增
3,如果有路障
m[i][j]=0
4,边界问题
如果左上角为1则m[0][0]=0,否则为1
5,最上水平的位置只能从左往右,最左垂直位置只能从上往下
故 m[i][0]=m[i-1][0],m[0][j]=m[0][j-1]
如果有路障 m[i][0]=0,m[0][j]=0
func uniquePathsWithObstacles(obstacleGrid [][]int) int {
if len(obstacleGrid)==0{
return 0
}
m:=make([][]int,len(obstacleGrid))
for i:=0;i<len(obstacleGrid);i++{
m[i]=make([]int,len(obstacleGrid[0]))
}
if obstacleGrid[0][0]==1{
return 0
}
m[0][0]=1
for i:=1;i<len(obstacleGrid);i++{
if obstacleGrid[i][0]==1{
m[i][0]=0
}else{
m[i][0]=m[i-1][0]
}
}
for j:=1;j<len(obstacleGrid[0]);j++{
if obstacleGrid[0][j]==1{
m[0][j]=0
}else{
m[0][j]=m[0][j-1]
}
}
for i:=1;i<len(obstacleGrid);i++{
for j:=1;j<len(obstacleGrid[0]);j++{
if obstacleGrid[i][j]==1{
m[i][j]=0
}else{
m[i][j]=m[i-1][j]+m[i][j-1]
}
}
}
return m[len(obstacleGrid)-1][len(obstacleGrid[0])-1]
}边栏推荐
猜你喜欢

mui中使用多级选择器实现省市区联动
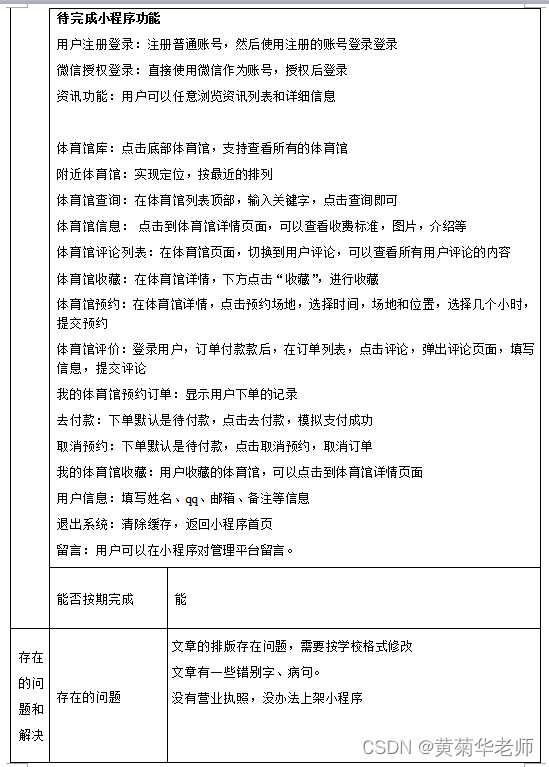
Wechat Gymnasium Appointment Mini Program Graduation Design Finished Works (7) Mid-term Inspection Report

全面认识二极管,一篇文章就够了
Flink学习9:配置idea开发flink-Scala程序环境
腾讯架构师是如何解释:Redis高性能通信的原理(精华版)
什么是SVN(Subversion)?
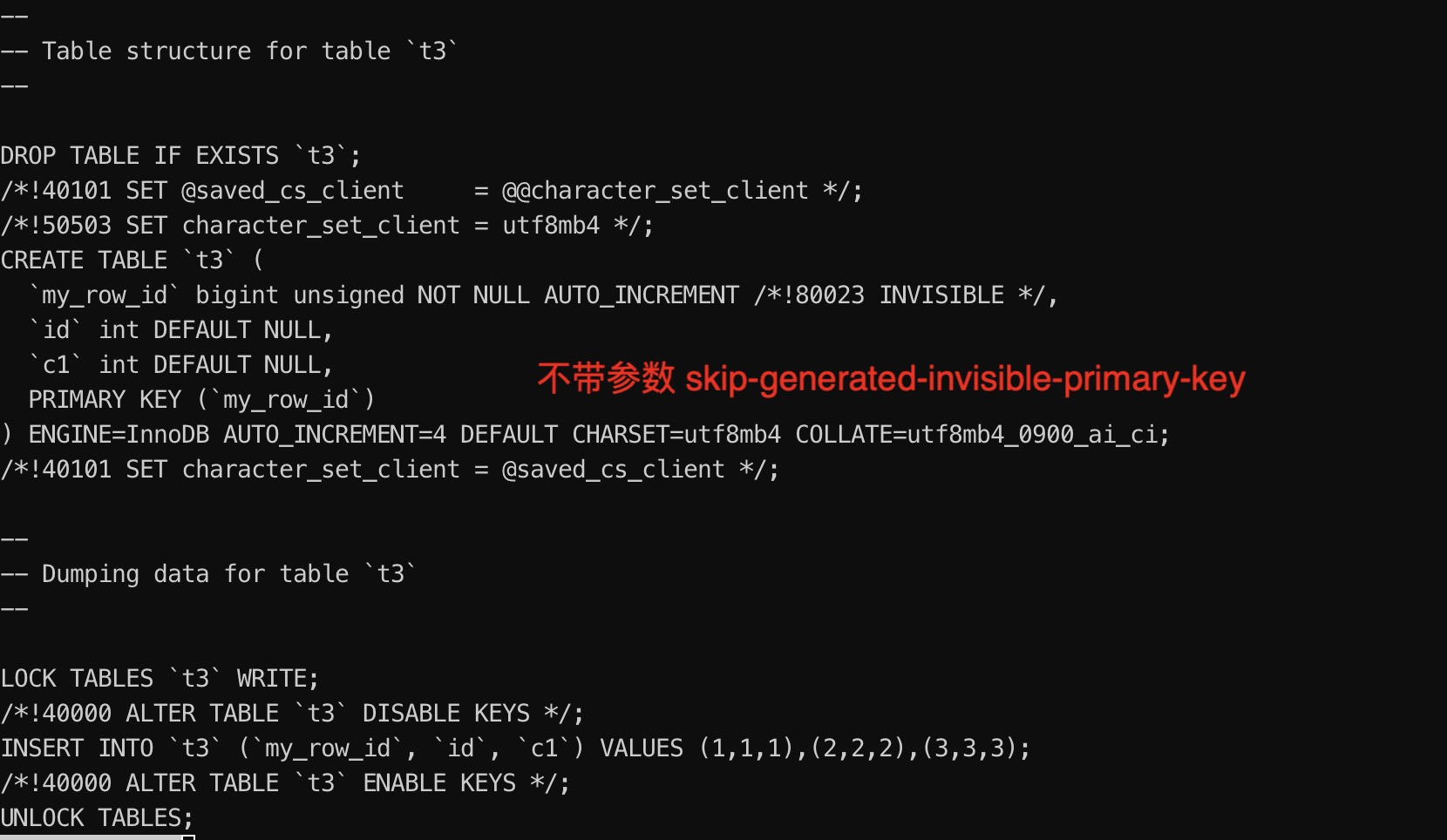
新特性解读 | MySQL 8.0 GIPK 不可见主键

Wechat Gymnasium Appointment Mini Program Graduation Design Finished Works Mini Program Graduation Design Finished Work (6) Question Opening Reply PPT

发挥云网融合优势,天翼云为政企铺设数字化转型跑道
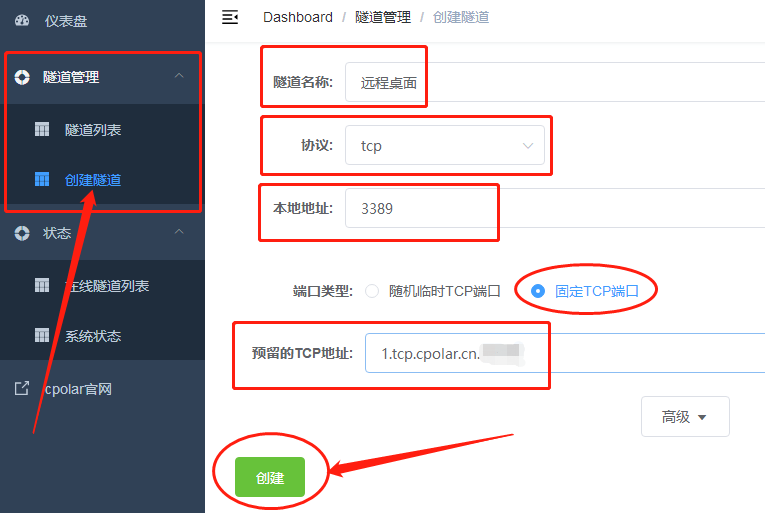
cpolar应用实例之多设备数据采集
随机推荐
2021年下半年软件设计师上午真题
shell中awk命令的if条件语句引入外置变量
golang源码分析(8):m、p、g、shedt、sudog
Several common cross-domain solutions
图解LeetCode——622. 设计循环队列(难度:中等)
executeScript异步执行的时候没有返回值的原因
Ubuntu系统下用docker安装oracle
什么是SVN(Subversion)?
全面认识二极管,一篇文章就够了
[C Language Brush Questions] Three Questions for Getting Started with Pointers | String Length, String Copy, Two Number Swap
FP6606CLP5 SOP-8 USB Type-C和PD充电控制器
在线文档Sheet技术解析
SQL 正则解析手机号码提供商
H5网页播放器EasyPlayer.js播放器界面的加载效果无法消失是什么原因?
docker安装Oracle之后常用的一些命令
织梦自定义表单添加全选和全不选功能按钮
分布式 | dble 启动的时候做了什么之配置检测
golang源码分析(7):chan
golang源码分析(4):select
究极异常处理逻辑——多层次异常的处理顺序