当前位置:网站首页>POJ 1465 Multiple(用BFS求能组成的n的最小倍数)
POJ 1465 Multiple(用BFS求能组成的n的最小倍数)
2022-08-03 18:23:00 【51CTO】
题目地址: 点击打开链接
题意:给一个数n,接着给m个数,用给已知的m个数组成的数最小的能被n整除的数是多少(其中m个数可以重复使用)
思路:和HDU1226有点相似,只不过比那道题简单,这里面m的数值没有说明,但是可以猜出来,问题的解空间是m^m,所以开一个大小为50的数组足够了,组成的数可以很大,必须不断取模,而且解空间太大,必须用同余减枝,而且必须减枝,否则第二个测试案例就出错误,因为程序会陷入死循环,假设A%N==B%N(设A<B),那么只取前面的数即可,因为前面的数小。本质就是求l%n==0,问最小的l是多少,假设组成l的数为A和B,则求(A%N+B)%N ==0,注意B不能对n取余,看代码注释掉的部分,会造成RE,没搞明白为啥,只搞明白有一种情况会出错,如m个数中有一个数和n相同,提前对m个数组取模会造成错误
AC代码:
边栏推荐
- Shell编程案例
- 揭秘deepin 23,从这里开始!
- ASA归因:如何评估关键词的投放价值
- cdc抽取mysql整个实例的binlog,有没有方案通过配置的方式将这些库表拆开分发到kafka
- Oracle备份的几种方式
- 什么是鉴权?一篇文章带你了解postman的多种方式
- China Hashpower Conference Ascension Kunpeng Ecological Forum was held; Kuaishou established an independent to B business department…
- Intelligent security contract - delegatecall (2)
- es6新增-Promise详解(异步编程的解决方案1)
- warnings.warn(“Title is more than 31 characters. Some applications may not be able to read the file
猜你喜欢
随机推荐
NLP范式新变化:Prompt
NLP的Taskflow API
Postgresql 备份大小情况!
Share 14 JS functions you must know
sys文件系统
WPF 实现柱形统计图
Install porterLB
flink-sql 客户端 可以设置并行度 吗?断开算子链
【刻意练习观后管】刻意练习
【汇编语言02】第2章 寄存器——理论知识
高等数学---第十章无穷级数---常数项级数
Cyanine5.5 alkyne|Cy5.5 alkyne|1628790-37-3|Cy5.5-ALK
Higher mathematics - chapter ten infinite series - constant term series
【汇编语言03】第2章 寄存器——实验1:查看CPU和内存,用机器指令和汇编指令编程
使用安全浏览器将网页保存为pdf的方法步骤
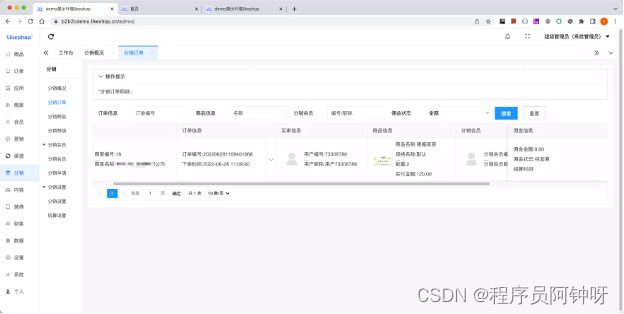
多商户商城系统功能拆解21讲-平台端分销订单
云GPU如何安装和启动VNC远程桌面服务?
【白话模电2】二极管特性和分类
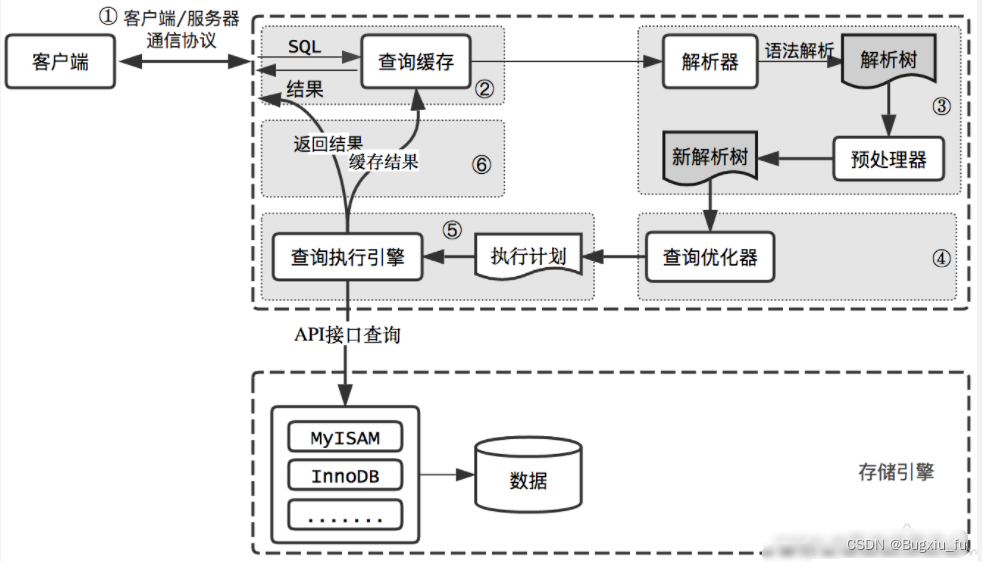
Execution plan of mysql
调用EasyCVR云台控制接口时,因网络延迟导致云台操作异常该如何解决?