当前位置:网站首页>吴恩达机器学习课后习题——逻辑回归
吴恩达机器学习课后习题——逻辑回归
2022-07-26 04:10:00 【一舟yz】
机器学习课后作业-逻辑回归
逻辑回归
逻辑回归算法,是一种给分类算法,这个算法的实质是:它输出值永远在0到 1 之间。
将要构建一个逻辑回归模型来预测,某个学生是否被大学录取。设想你是大学相关部分的管理者,想通过申请学生两次测试的评分,来决定他们是否被录取。现在你拥有之前申请学生的可以用于训练逻辑回归的训练样本集。对于每一个训练样本,你有他们两次测试的评分和最后是被录取的结果。为了完成这个预测任务,我们准备构建一个可以基于两次测试评分来评估录取可能性的分类模型。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
path = 'ex2data1.txt'
data = pd.read_csv(path,names=['Exam1','Exam2','Admitted'])
data.head()
| Exam1 | Exam2 | Admitted | |
|---|---|---|---|
| 0 | 34.623660 | 78.024693 | 0 |
| 1 | 30.286711 | 43.894998 | 0 |
| 2 | 35.847409 | 72.902198 | 0 |
| 3 | 60.182599 | 86.308552 | 1 |
| 4 | 79.032736 | 75.344376 | 1 |
# .isin是pandas中DataFrame的布尔索引,可以用满足布尔条件的列值来过滤数据
positive = data[data['Admitted'].isin([1])]
negative = data[data['Admitted'].isin([0])]
fig,ax = plt.subplots(figsize=(12,8))
ax.scatter(positive['Exam1'],positive['Exam2'],s=80,c='g',marker='o',label='Admitted') # s表示画的点的大小
ax.scatter(negative['Exam1'],negative['Exam2'],s=80,c='r',marker='x',label='NOtAdmitted')
ax.legend(loc=1) # 标签位置 右上角
ax.set_xlabel("Exam1Score")
ax.set_ylabel("Exam2Score")
plt.show()

sigmoid 函数
g 代表一个常用的逻辑函数(logistic function)为S形函数(Sigmoid function),公式为:
g ( z ) = 1 1 + e − z g\left( z \right)=\frac{1}{1+{ {e}^{-z}}}\\ g(z)=1+e−z1
合起来,我们得到逻辑回归模型的假设函数:
h θ ( x ) = 1 1 + e − θ T X { {h}_{\theta }}\left( x \right)=\frac{1}{1+{ {e}^{-{ {\theta }^{T}}X}}} hθ(x)=1+e−θTX1
def sigmoid(z):
# 当np.exp()的参数传入的是一个向量时,其返回值是该向量内所以元素值分别进行e^{x} 求值后的结果,所构成的一个列表返回给调用处。
return 1 / (1+np.exp(-z))
# 测试上述函数
nums = np.arange(-5,5)
fig,ax = plt.subplots(figsize=(12,8))
ax.plot(nums,sigmoid(nums),c='r')
plt.show()

编写代价函数来评估结果。
代价函数:
J ( θ ) = 1 m ∑ i = 1 m [ − y ( i ) log ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{[-{ {y}^{(i)}}\log \left( { {h}_{\theta }}\left( { {x}^{(i)}} \right) \right)-\left( 1-{ {y}^{(i)}} \right)\log \left( 1-{ {h}_{\theta }}\left( { {x}^{(i)}} \right) \right)]} J(θ)=m1i=1∑m[−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i)))]
如果用“*”来做矩阵乘法,要求两边都是matrix类型,若用dot实现矩阵乘法,要求是ndarray类型,并且前一个ndarray的列数等于后一个的行数
def cost(theta, X, y):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
return np.sum(first - second) / (len(X))
# 数据处理
try:
data.insert(-0,'Ones',1)
except:
pass
cols = data.shape[1]
X = data.iloc[:,0:cols-1]
y = data.iloc[:,cols-1:cols]
X = np.array(X.values)
y = np.array(y.values)
theta = np.zeros(X.shape[1])
X.shape,y.shape,theta.shape
((100, 3), (100, 1), (3,))
cost(theta, X, y)
0.6931471805599453
梯度下降法
- 这是批量梯度下降(batch gradient descent)
- 转化为向量化计算: 1 m X T ( S i g m o i d ( X θ ) − y ) \frac{1}{m} X^T( Sigmoid(X\theta) - y ) m1XT(Sigmoid(Xθ)−y)
∂ J ( θ ) ∂ θ j = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial J\left( \theta \right)}{\partial { {\theta }_{j}}}=\frac{1}{m}\sum\limits_{i=1}^{m}{({ {h}_{\theta }}\left( { {x}^{(i)}} \right)-{ {y}^{(i)}})x_{_{j}}^{(i)}} ∂θj∂J(θ)=m1i=1∑m(hθ(x(i))−y(i))xj(i)
# 求梯度
def gradient(theta, X, y):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
parameters = int(theta.ravel().shape[1])
grad = np.zeros(parameters)
error = sigmoid(X * theta.T) - y
for i in range(parameters):
term = np.multiply(error, X[:,i])
grad[i] = np.sum(term) / len(X)
return grad
gradient(theta, X, y)
array([ -0.1 , -12.00921659, -11.26284221])
# 梯度下降
def gradientDesent(theta, X, y,alpha,iters):
costs = np.zeros(iters)
temp = np.zeros(len(theta))
for i in range(iters): # 迭代
temp = theta - alpha*gradient(theta,X,y)
theta = temp
costs[i] = cost(theta,X,y)
return theta,costs
可视化
theta,costs = gradientDesent(theta, X, y,0.001,1000)
# theta,costs[-1]
print(theta)
print(costs[-1])
fig,ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(1000),costs,'r')
ax.set_xlabel("Iterations")
ax.set_ylabel("Cost")
ax.set_title("Error vs. Iteration")
plt.show()
[-0.06946097 0.01090733 0.00099135]
0.6249857589104834

参数拟合—高级优化算法
import scipy.optimize as opt
result = opt.minimize(fun=cost,x0=theta,args=(X,y),jac=gradient,method='TNC')
result #result.x 为拟合的θ参数
fun: 0.20349910741165939
jac: array([-3.40179217e-05, -4.36399521e-04, -2.11471183e-04])
message: 'Converged (|f_n-f_(n-1)| ~= 0)'
nfev: 25
nit: 10
status: 1
success: True
x: array([-25.25870569, 0.20700684, 0.20226198])
cost(result.x, X, y) #result.x 为拟合的θ参数
0.20349910741165939
根据训练的模型参数进行预测
def predict(X,theta): #对数据进行预测
return (sigmoid(X @ theta.T)>=0.5).astype(int) #实现变量类型转换
from sklearn.metrics import classification_report
y_pred = predict(X,result.x)
print(classification_report(y,y_pred))
precision recall f1-score support
0 0.87 0.85 0.86 40
1 0.90 0.92 0.91 60
accuracy 0.89 100
macro avg 0.89 0.88 0.88 100
weighted avg 0.89 0.89 0.89 100
可视化决策边界
已经得到了θ的参数,将Xθ取0即可得到对应的决策边界函数
θ 0 + θ 1 x 1 + θ 2 x 2 = 0 \theta_0+\theta_1x_1+\theta_2x_2=0 θ0+θ1x1+θ2x2=0
θ 0 θ 2 + θ 1 θ 2 x 1 + x 2 = 0 \frac {\theta_0} {\theta_2}+\frac {\theta_1} {\theta_2}x_1+x_2=0 θ2θ0+θ2θ1x1+x2=0
x 2 = − θ 0 θ 2 − θ 1 θ 2 x 1 x_2=-\frac{\theta_0}{\theta2}-\frac{\theta_1}{\theta_2}x_1 x2=−θ2θ0−θ2θ1x1
#先绘制原来数据
positive = data[data['Admitted'].isin([1])]
negative = data[data['Admitted'].isin([0])]
fig,ax = plt.subplots(figsize=(12,8))
ax.scatter(positive['Exam1'],positive['Exam2'],s=80,c='g',marker='o',label='Admitted') # s表示画的点的大小
ax.scatter(negative['Exam1'],negative['Exam2'],s=80,c='r',marker='x',label='NOtAdmitted')
ax.legend(loc=1) # 标签位置 右上角
ax.set_xlabel("Exam1Score")
ax.set_ylabel("Exam2Score")
#绘制决策边界
theta_res = result.x
exam_x = np.arange(X[:,1].min(),X[:,1].max(),0.01)
theta_res = - theta_res/theta_res[2] #获取函数系数θ_0/θ_2 θ_0/θ_2
print(theta_res)
exam_y = theta_res[0]+theta_res[1]*exam_x
ax.plot(exam_x,exam_y)
plt.show()
[124.88113404 -1.02345898 -1. ]

正则化逻辑回归
path = 'ex2data2.txt'
data2 = pd.read_csv(path, header=None, names=['Test 1', 'Test 2', 'Accepted'])
data2.head()
| Test 1 | Test 2 | Accepted | |
|---|---|---|---|
| 0 | 0.051267 | 0.69956 | 1 |
| 1 | -0.092742 | 0.68494 | 1 |
| 2 | -0.213710 | 0.69225 | 1 |
| 3 | -0.375000 | 0.50219 | 1 |
| 4 | -0.513250 | 0.46564 | 1 |
positive = data2[data2['Accepted'].isin([1])]
negative = data2[data2['Accepted'].isin([0])]
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(positive['Test 1'], positive['Test 2'], s=50, c='b', marker='o', label='Accepted')
ax.scatter(negative['Test 1'], negative['Test 2'], s=50, c='r', marker='x', label='Rejected')
ax.legend()
ax.set_xlabel('Test 1 Score')
ax.set_ylabel('Test 2 Score')
plt.show()

# 通过特征映射,来找到合适的多项式。
degree = 5
x1 = data2['Test 1']
x2 = data2['Test 2']
data2.insert(3, 'Ones', 1)
for i in range(1, degree):
for j in range(0, i):
data2['F' + str(i) + str(j)] = np.power(x1, i-j) * np.power(x2, j)
data2.drop('Test 1', axis=1, inplace=True)
data2.drop('Test 2', axis=1, inplace=True)
data2.head()
| Accepted | Ones | F10 | F20 | F21 | F30 | F31 | F32 | F40 | F41 | F42 | F43 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 0.051267 | 0.002628 | 0.035864 | 0.000135 | 0.001839 | 0.025089 | 0.000007 | 0.000094 | 0.001286 | 0.017551 |
| 1 | 1 | 1 | -0.092742 | 0.008601 | -0.063523 | -0.000798 | 0.005891 | -0.043509 | 0.000074 | -0.000546 | 0.004035 | -0.029801 |
| 2 | 1 | 1 | -0.213710 | 0.045672 | -0.147941 | -0.009761 | 0.031616 | -0.102412 | 0.002086 | -0.006757 | 0.021886 | -0.070895 |
| 3 | 1 | 1 | -0.375000 | 0.140625 | -0.188321 | -0.052734 | 0.070620 | -0.094573 | 0.019775 | -0.026483 | 0.035465 | -0.047494 |
| 4 | 1 | 1 | -0.513250 | 0.263426 | -0.238990 | -0.135203 | 0.122661 | -0.111283 | 0.069393 | -0.062956 | 0.057116 | -0.051818 |
regularized cost(正则化代价函数)
J ( θ ) = 1 m ∑ i = 1 m [ − y ( i ) log ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{[-{ {y}^{(i)}}\log \left( { {h}_{\theta }}\left( { {x}^{(i)}} \right) \right)-\left( 1-{ {y}^{(i)}} \right)\log \left( 1-{ {h}_{\theta }}\left( { {x}^{(i)}} \right) \right)]}+\frac{\lambda }{2m}\sum\limits_{j=1}^{n}{\theta _{j}^{2}} J(θ)=m1i=1∑m[−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2
def costReg(theta, X, y, learningRate):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
reg = (learningRate / (2 * len(X))) * np.sum(np.power(theta[:,1:theta.shape[1]], 2))
return np.sum(first - second) / len(X) + reg
如果我们要使用梯度下降法令这个代价函数最小化,正则化不包含 θ 0 { {\theta }_{0}} θ0 ,所以梯度下降算法将分两种情形:
R e p e a t u n t i l c o n v e r g e n c e { θ 0 : = θ 0 − a 1 m ∑ i = 1 m [ h θ ( x ( i ) ) − y ( i ) ] x 0 ( i ) θ j : = θ j − a 1 m ∑ i = 1 m [ h θ ( x ( i ) ) − y ( i ) ] x j ( i ) + λ m θ j } R e p e a t \begin{align} & Repeat\text{ }until\text{ }convergence\text{ }\!\!\{\!\!\text{ } \\ & \text{ }{ {\theta }_{0}}:={ {\theta }_{0}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{[{ {h}_{\theta }}\left( { {x}^{(i)}} \right)-{ {y}^{(i)}}]x_{_{0}}^{(i)}} \\ & \text{ }{ {\theta }_{j}}:={ {\theta }_{j}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{[{ {h}_{\theta }}\left( { {x}^{(i)}} \right)-{ {y}^{(i)}}]x_{j}^{(i)}}+\frac{\lambda }{m}{ {\theta }_{j}} \\ & \text{ }\!\!\}\!\!\text{ } \\ & Repeat \\ \end{align} Repeat until convergence { θ0:=θ0−am1i=1∑m[hθ(x(i))−y(i)]x0(i) θj:=θj−am1i=1∑m[hθ(x(i))−y(i)]xj(i)+mλθj } Repeat
对上面的算法中 j=1,2,…,n 时的更新式子进行整理可得:
θ j : = θ j ( 1 − a λ m ) − a 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) { {\theta }_{j}}:={ {\theta }_{j}}(1-a\frac{\lambda }{m})-a\frac{1}{m}\sum\limits_{i=1}^{m}{({ {h}_{\theta }}\left( { {x}^{(i)}} \right)-{ {y}^{(i)}})x_{j}^{(i)}} θj:=θj(1−amλ)−am1i=1∑m(hθ(x(i))−y(i))xj(i)
def gradientReg(theta, X, y, learningRate):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
parameters = int(theta.ravel().shape[1])
grad = np.zeros(parameters)
error = sigmoid(X * theta.T) - y
for i in range(parameters):
term = np.multiply(error, X[:,i])
if (i == 0):
grad[i] = np.sum(term) / len(X)
else:
grad[i] = (np.sum(term) / len(X)) + ((learningRate / len(X)) * theta[:,i])
return grad
# 初始化
# set X and y (remember from above that we moved the label to column 0)
cols = data2.shape[1]
X2 = data2.iloc[:,1:cols]
y2 = data2.iloc[:,0:1]
# convert to numpy arrays and initalize the parameter array theta
X2 = np.array(X2.values)
y2 = np.array(y2.values)
theta2 = np.zeros(X2.shape[1])
# 初始化学习率
learningRate = 1
costReg(theta2, X2, y2, learningRate)
0.6931471805599454
gradientReg(theta2, X2, y2, learningRate)
array([0.00847458, 0.01878809, 0.05034464, 0.01150133, 0.01835599,
0.00732393, 0.00819244, 0.03934862, 0.00223924, 0.01286005,
0.00309594])
高级优化算法拟合参数θ
result2 = opt.fmin_tnc(func=costReg, x0=theta2, fprime=gradientReg, args=(X2, y2, learningRate))
result2
(array([ 0.53010248, 0.29075567, -1.60725764, -0.5821382 , 0.01781027,
-0.21329508, -0.40024142, -1.37144139, 0.02264303, -0.9503358 ,
0.0344085 ]),
22,
1)
# 可以使用高级Python库像scikit-learn来解决这个问题
from sklearn import linear_model#调用sklearn的线性回归包
model = linear_model.LogisticRegression(penalty='l2', C=1.0)
model.fit(X2, y2.ravel())
边栏推荐
- Mantium 如何在 Amazon SageMaker 上使用 DeepSpeed 实现低延迟 GPT-J 推理
- 荐书 |《学者的术与道》:写论文是门手艺
- Go plus security: an indispensable security ecological infrastructure for build Web3
- Where does international crude oil open an account, a formal, safe and secure platform
- 电商运营小白,如何快速入门学习数据分析?
- laravel8 实现接口鉴权封装使用JWT
- The PHP Eval () function can run a string as PHP code
- Matrix and Gauss elimination [matrix multiplication, Gauss elimination, solving linear equations, solving determinants] the most detailed in the whole network, with examples and sister chapters of 130
- 2.9.4 Ext JS的布尔对象类型处理及便捷方法
- Implementation of distributed lock
猜你喜欢

Overview of wavelet packet transform methods

【云原生】谈谈老牌消息中间件ActiveMQ的理解

PathMatchingResourcePatternResolver解析配置文件 资源文件
What are the duplicate check rules for English papers?

How to transfer English documents to Chinese?

软模拟光栅化渲染器
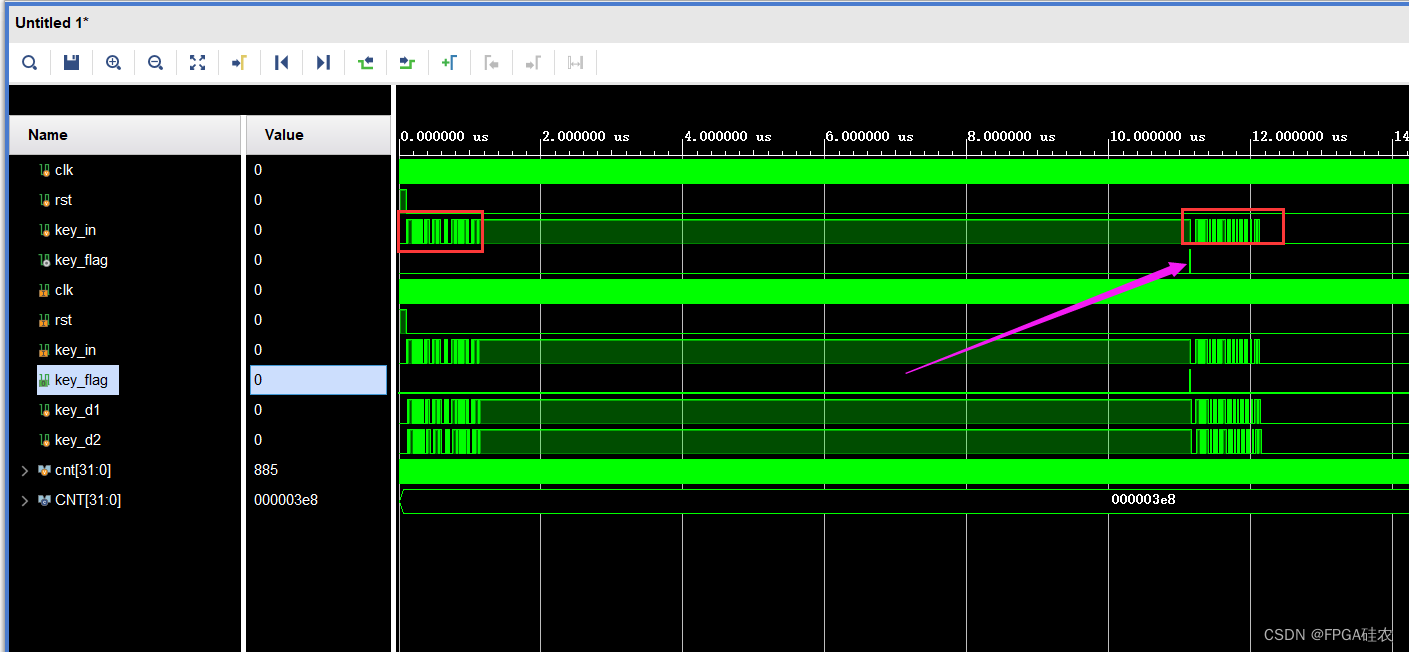
Verilog implementation of key dithering elimination

华为高层谈 35 岁危机,程序员如何破年龄之忧?
零售连锁门店收银系统源码管理商品分类的功能逻辑分享

redux
随机推荐
Sorting and searching
Go plus security: an indispensable security ecological infrastructure for build Web3
Dracoo Master天龙卡牌大师
按键消抖的Verilog实现
构建关系抽取的动词源
Pits encountered by sdl2 OpenGL
Functions of anonymous functions
Introduction to UFS CLK gate
Working ideas of stability and high availability guarantee
Implementation of distributed lock
【读书笔记->数据分析】BDA教材《数据分析》书籍介绍
This article takes you to graph transformers
How does redis implement persistence? Explain the AOF trigger mechanism and its advantages and disadvantages in detail, and take you to quickly master AOF
(translation) the button position convention can strengthen the user's usage habits
(translation) timing of website flow chart and user flow chart
APISIX 在 API 和微服务领域的探索
2022杭电多校 Bowcraft
荐书丨《教育心理学》:送给明日教师的一本书~
1311_硬件设计_ICT概念、应用以及优缺点学习小结
Apple removed the last Intel chip from its products