当前位置:网站首页>树和二叉树
树和二叉树
2022-08-04 05:31:00 【小羊的预备程序员】
目录
一、树的基本概念
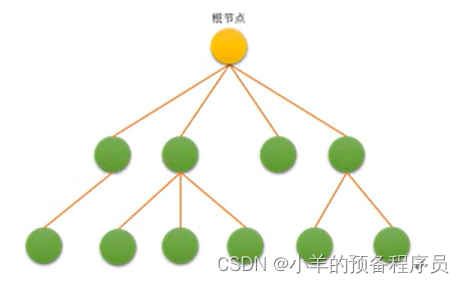
树的定义:
由一个或多个(n≥0)结点组成的有限集合T ,有且仅有一个结点称为根( root ) ,当n>1
时,其余的结点分为m(m≥0)个互不相交的有限集合T1,T2 ,... ,Tm。每个集合本身
又是棵树,被称作这个根的子树。
树的结构特点
■ 非线性结构,有一个直接前驱,但可能有多个直接后继( 1:n )
■ 树的定义具有递归性,树中还有树。
■ 树可以为空,即节点个数为0。
若干术语:
■ 根 → 即根节点(没有前驱)
■ 叶子 → 即终端节点(没有后继)
■ 森林 →指m棵不相交的树的集合(例如删除A后的字数个数)
■ 有序树 →结点各子树从左至右有序,不能互换(左为第一)
■ 无序树 →结点各子树可互换位置。
■ 双亲 →即上层的那个结点(直接前驱) parent
■ 孩子 →即下层结点的子树(直接后迷) child
■ 兄弟 →同一双亲下的同层结点(孩子之间互称兄弟) sibling-
■ 堂兄弟 →即双亲位于同一层的结点(但并非同一双亲) cousinv
■ 祖先 →即从根到该结点所经分支的所有结点
■ 子孙 →即该结点下层子树中的任一结点
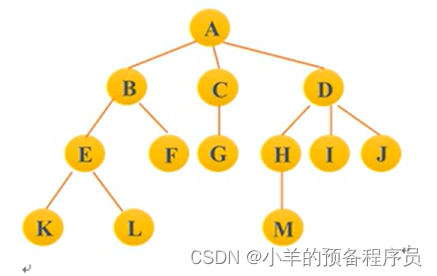
■ 结点 →即树的数据元素
■ 结点的度 →结点挂接的子树数(有几个直接后继就是几度)
■ 结点的层次 →从根到该结点的层数(根结点算第一层)
■ 终端结点 →即度为0的结点,即叶子
■ 分支结点 →除树根以外的结点(也称为内部结点)
■ 树的度 →所有结点度中的最大值(Max{各结点的度})
■ 树的深度(或高度) →指所有结点中最大的层数(Max{各结点的层次})
上图中的结点数=13,树的度= 3,树的深度=4
二、树的表示法
1、图形表示法
事物之间的逻辑关系可以通过树的形式很直观的表示出来,如下图:
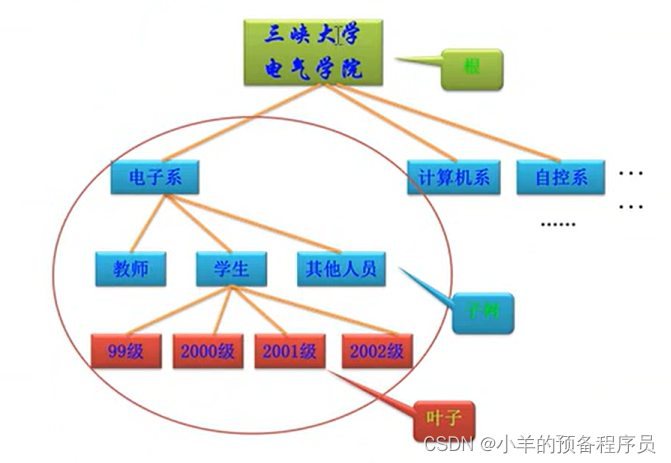
2、广义表表示法

用广义表表示法表示上图
中国(河北(保定,石家庄),广东(广州,东莞),山东(青岛,济南))
跟作为由子树森林组成的表的名字写在表的左边
3、左孩子右兄弟表示法
左孩子右兄弟表示法可以将一颗多叉树转化为一颗二叉树
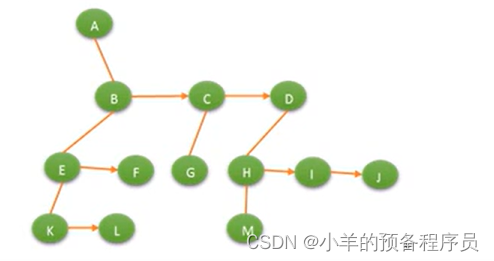
三、二叉树的概念
1、二叉树的基本概念
定义:
n ( n≥0)个结点的有限集合,由一个根结点以及两棵互不相交的、分别称为左子树和
右子树的二叉树组成。
逻辑结构:
一对二(1:2)
基本特征:
■ 每个节点最多只有两颗子树(不存在度大于2的结点)
■ 左子树和右子树次序不能颠倒(有序树)
基本形态:

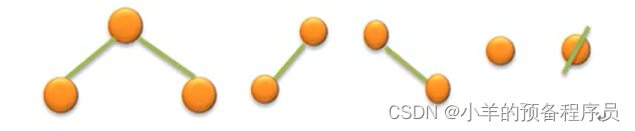
二叉树性质:
■ 性质1:在二叉树的第i层之多有2^(i - 1)个结点(i > 0)
■ 性质2:深度为k的二叉树至多有2^k - 1个结点(k > 0)(1+2+4+...+2^(k-1))
■ 性质3:对于任何一颗二叉树,若度为2的节点数有n2个,则叶子数(n0)必定为n2+1(即n0 = n2 + 1)
概念解释:
〇 满二叉树
一颗深度为k且有2^k - 1个结点的二叉树
特点:每层都“充满”了结点
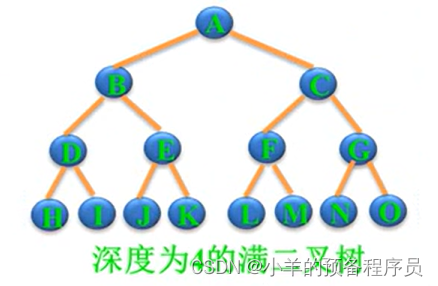
〇 完全二叉树
除最后一层外,每一层上的结点数均达到最大值;在最后一层上只缺少右边的若干结点。
■ 性质4:具有n个结点的完全二叉树的深度必为| |+1
|+1
( log2(15)点击15 log / 2 log =)
■ 性质5:对完全二叉树(前提),若从上至下、从左至右编号,则编号为i的结点,其左孩子
编号必为2i,其右孩子编号必为2i+1;其双亲的编号必为i/2 ( i=1时为根,除外)
2、二叉树的表示
二叉链表示法
一般从根结点开始存储。相应地,访问树中结点时也只能从根开始。
■ 存储结构
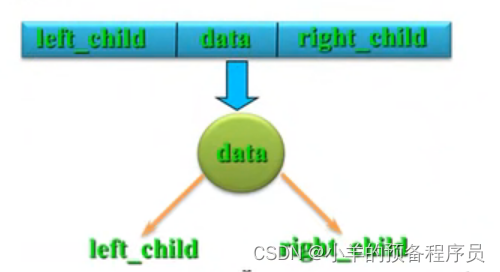
■ 结点数据类型定义
typedef struct BiTNode
{
int data;
struct BitNode * lchild, * rchild;
}BitNode, * BitTree三叉链表表示法
■ 存储结构

每个结点有三个指针域,其中两个分别指向子节点(左孩子,右孩子),还有一个指针指向该节点的父节点。
■ 结点的数据类型定义
//三叉链表
typedef struct TriNOde
{
int data;
//左右孩子指针
struct TriNode * lchild,* rchild
struct TriNode * parent
}TriNode, * TriTree3、二叉树的遍历
遍历定义:
指按某条搜索路线遍历每个结点且不重复(又称周游)。
遍历用途:
它是树插入、删除、修改、查找和排序运算的前提,是二叉树一切运算的基础和核心。
遍历方法:
牢记一种约定,对每个结点的查看都是“先左后右”。
限定先左后右,树的遍历有三种方案:

■ DLR —— 先序遍历,即先根再左再右
■ LDR —— 中序遍历,即先左再根再右
■ LRD —— 后序遍历,即先左再右再根
注:“先、中、后”的意思是指访问的结点D是先于子树出现还是后于子树出现。

4、二叉树的编程实践
二叉树的数据结构
struct BinaryNode
{
//数据
char ch;
//指针域
struct BinaryNode * lChild;
struct BinaryNode * rChild;
};(1)二叉树的递归遍历
//先序遍历
void recursion(struct BinaryNode * root)
{
if (root == NULL)
{
return;
}
printf("%c ", root->ch);
recursion(root->lChild);
recursion(root->rChild);
}//中序遍历
void recursion(struct BinaryNode * root)
{
if (root == NULL)
{
return;
}
recursion(root->lChild);
printf("%c ", root->ch);
recursion(root->rChild);
}
//后序遍历
void recursion(struct BinaryNode * root)
{
if (root == NULL)
{
return;
}
recursion(root->lChild);
recursion(root->rChild);
printf("%c ", root->ch);
}(2)求树的叶子数
//求树的叶子数 思路:当找到的结点没有后继结点的时候就是叶子,计数器+1
void Get_Tree_Leaf_Num(struct BinaryNode * root, int * num)
{
if (root == NULL)
{
return;
}
if (root->lChild == NULL && root->rChild == NULL)
{
(*num)++;
}
Get_Tree_Leaf_Num(root->lChild, num);
Get_Tree_Leaf_Num(root->rChild, num);
}(3)求树的高度
//求树的高度 思路:左子树的高度与右子树的高度相比,取最大值+1就是该树的高度
int Get_Tree_Height(struct BinaryNode * root)
{
if (root == NULL)
{
return 0;
}
int lheight = Get_Tree_Height(root->lChild);
int rheight = Get_Tree_Height(root->rChild);
int height = lheight > rheight ? lheight + 1 : rheight + 1;
return height;
}(4)拷贝二叉树
struct BinaryNode * copy_tree(struct BinaryNode * root)
{
if (root == NULL)
{
return NULL;
}
//拷贝左子树
struct BinaryNode * lChild = copy_tree(root->lChild);
//拷贝右子树
struct BinaryNode * rChild = copy_tree(root->rChild);
//让parent指向左右子树
struct BinaryNode * newroot = (struct BinaryNode *)malloc(sizeof(struct BinaryNode));
newroot->ch = root->ch;
newroot->lChild = lChild;
newroot->rChild = rChild;
return newroot;
}(5)释放二叉树
void free_tree(struct BinaryNode * root)
{
if (root == NULL)
{
return;
}
//先释放左子树
free_tree(root->lChild);
//再释放右子树
free_tree(root->rChild);
//然后释放根结点
//每次释放之前先打印要释放的根结点,验证结果
printf("%c ", root->ch);
free(root);
}(6)二叉树的非递归遍历
二叉树的非递归遍历方法与递归遍历设计数据结构不同,需要用到一个flag标志,并且需要用到栈来作为临时容器
struct BinaryNode
{
//数据
char ch;
//指针域
struct BinaryNode * lChild;
struct BinaryNode * rChild;
//标志
bool flag;
};后续实现只给核心代码,并说明自己遇到的问题
非递归函数实现
void nonrecursion(struct BinaryNode * root)
{
ST ps;
StackInit(&ps);
//1.根结点入栈
StackPush(&ps, root);
//2.只要栈中的元素个数大于0执行循环
while (StackSize(&ps) > 0)
{
//3.获取栈顶元素
struct BinaryNode * top = StackTop(&ps);
//防止子树为空,仍被视作一个结点进行下面的操作
if (top == NULL)
{
StackPop(&ps);
continue;
}
//4.出栈
StackPop(&ps);
//5.如果标志位真 直接输出 并且执行下一次循环 如果为假,将标志改为真
if (top->flag)
{
printf("%c ", top->ch);
continue;
}
else
{
top->flag = true;
}
//将右子树 左子树 根入栈
StackPush(&ps, top->rChild);
StackPush(&ps, top->lChild);
StackPush(&ps, top);
//然后执行下一次循环
}
}遇到的问题
在第一次实现完成后发现老是报终端错误,一开始误以为越界访问,但是仔细思索后我自己实现的栈容器有自动扩容的功能,错误原因并不是越界访问,而是我采用的二叉树的结构并不是满二叉树,会存在空的子树也会被top存储,后续判断top的flag标志位的时候top->flag存在空指针指向flag的问题报错,所以设置了一个检测过程解决问题
//防止子树为空,仍被视作一个结点进行下面的操作
if (top == NULL)
{
StackPop(&ps);
continue;
}运行结果
这里实现的是非递归先序排序,与我所用的树的输出结果吻合,实现完成
![]()

边栏推荐
- 深度学习理论——过拟合、欠拟合、正则化、优化器
- [开发杂项][调试]debug into kernel
- LeetCode_Dec_2nd_Week
- IEEE802.X协议族
- Golang environment variable settings (2)--GOMODULE & GOPROXY
- [English learning][sentence] good sentence
- Rules.make-适合在编辑模式下看
- LeetCode_Nov_4th_Week
- Copy Siege Lion 5-minute online experience MindIR format model generation
- LeetCode_22_Apr_4th_Week
猜你喜欢

Shell脚本执行的三种方式

The second official example analysis of the MOOSE platform - about creating a Kernel and solving the convection-diffusion equation
枚举和联合(自定义类型)-C语言
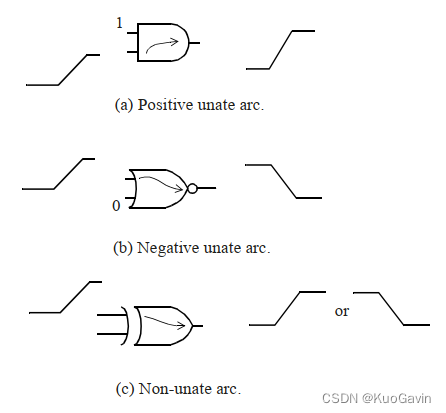
第二章 STA相关概念
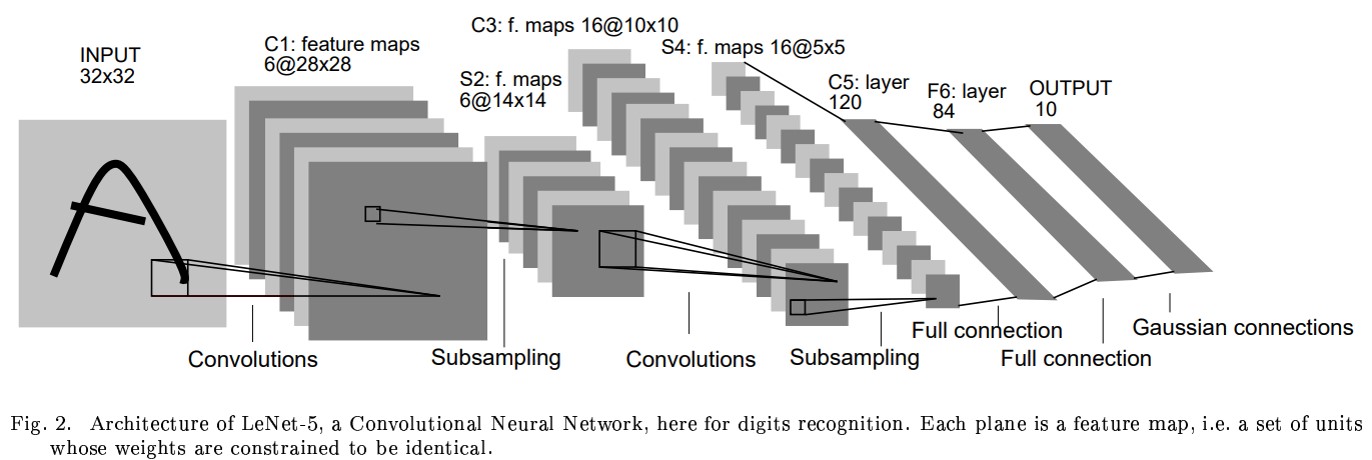
MNIST Handwritten Digit Recognition - Lenet-5's First Commercial Grade Convolutional Neural Network
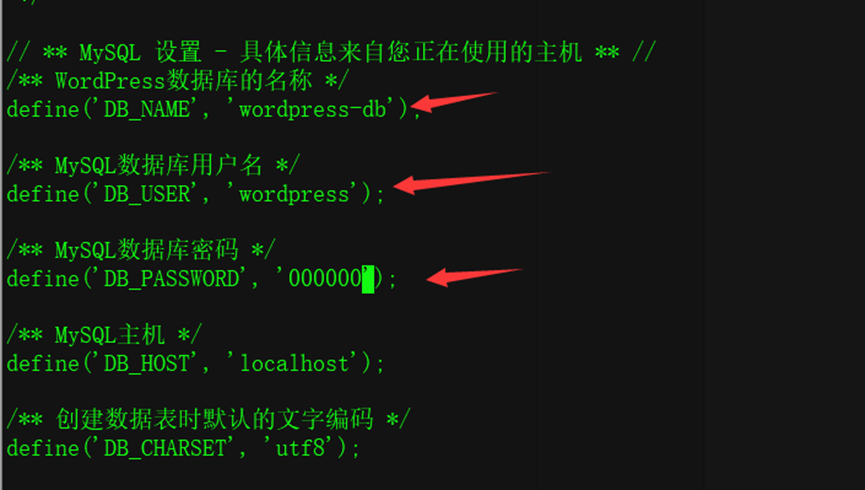
【五一专属】阿里云ECS大测评#五一专属|向所有热爱分享的“技术劳动者”致敬#

Pipe redirection

How to get started with MOOSE platform - an example of how to run the official tutorial
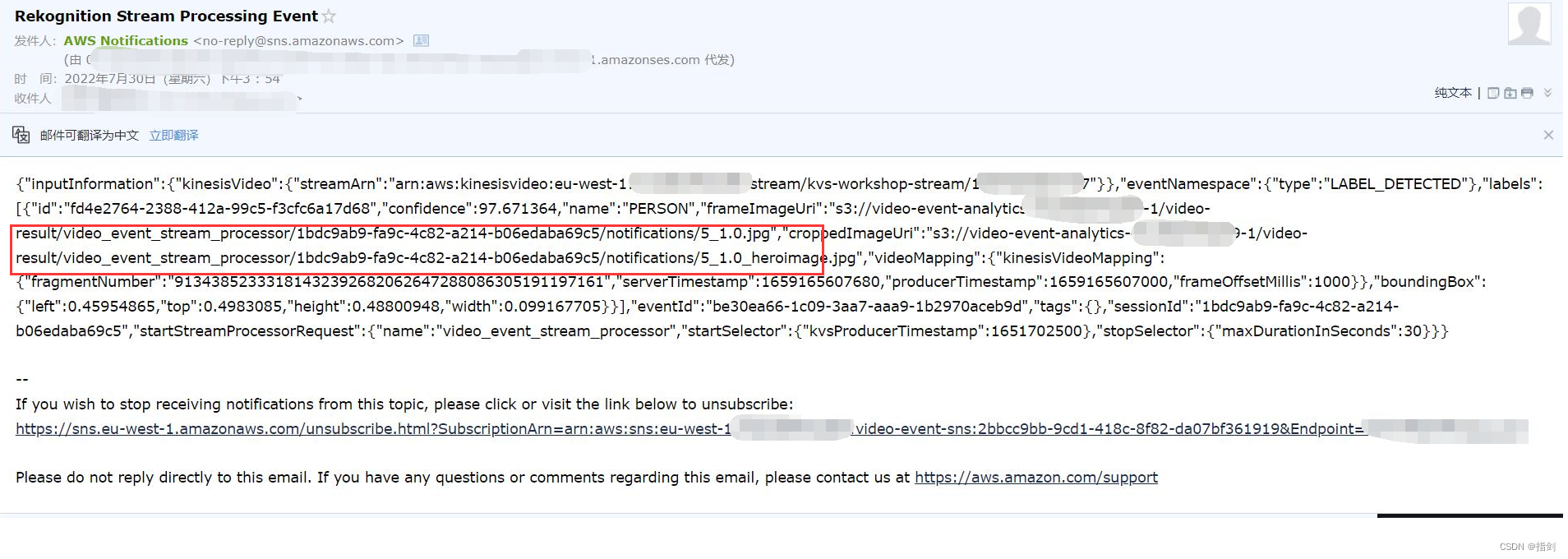
Amazon Cloud Technology Build On 2022 - AIot Season 2 IoT Special Experiment Experience

Tencent and NetEase have taken action one after another. What is the metaverse that is so popular that it is out of the circle?
随机推荐
安装MySQL的详细步骤
结构体内存对齐-C语言
抽象类、内部类和接口
LeetCode_22_Apr_4th_Week
Question 1000: Input two integers a and b, calculate the sum of a+b, this question is multiple sets of test data
MNIST Handwritten Digit Recognition - From Perceptrons to Convolutional Neural Networks
Implementation of CAS lock-free queue
在AWS-EC2中安装Minikube集群
AWS使用EC2降低DeepRacer的训练成本:DeepRacer-for-cloud的实践操作
LeetCode_Nov_1st_Week
Fabric v1.1 环境搭建
MNIST Handwritten Digit Recognition - Image Analysis Method for Binary Classification
Rules.make - suitable for viewing in edit mode
MNIST手写数字识别 —— 从感知机到卷积神经网络
MNIST手写数字识别 —— Lenet-5首个商用级别卷积神经网络
C语言数组的深度分析
MNIST handwritten digit recognition, sorted by from two to ten
tmux concept and usage
Code to celebrate the Dragon Boat Festival - Zongzi, your heart
多线程顺序输出
