当前位置:网站首页>UR3机器人运动学分析之正运动学分析
UR3机器人运动学分析之正运动学分析
2022-07-31 05:17:00 【G_Summer_Song】
前往我的博客阅读体验更佳:本文链接
UR3工业机器人是一个6自由度的连杆机器人,其结构图如下图所示:
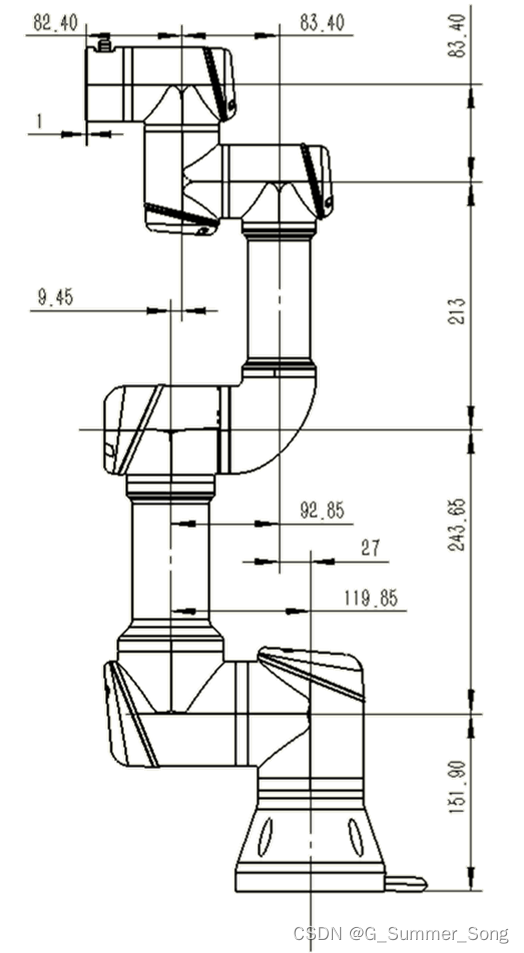
1 正运动学分析
1.1 建立机器人连杆坐标系
UR3机器人属于连杆机器人,对于一个连杆机器人来说,可以用四个参数:连杆长度 a i a_i ai,连杆扭角 α i \alpha_i αi,连杆距离 d i d_i di,关节转角 θ i \theta_i θi来描述。这四个参数即为连杆机器人的DH参数,在不同类型的连杆坐标系下,DH参数的含义有所不同。
连杆坐标系的建立有标准型DH法(SDH)建模和改进型DH法(MDH)建模两种方法,下面分别使用两种方法建立UR3机器人的连杆坐标系。
1.1.1 标准型DH法(SDH)建模
标准型DH法建模规则如下:
找出各关节轴,并画出这些轴线的延长线;
找 Z Z Z轴:与轴线重合, Z i − 1 Z_{i-1} Zi−1轴为关节 i i i的运动轴;
找 X X X轴:关节轴线相离时,在公垂线分析上定义 X X X轴,如果 a i a_i ai表示 Z i − 1 Z_{i-1} Zi−1与 Z Z Z之间的公垂线,则 X i X_i Xi的方向沿 a i a_i ai;关节轴线平行时,选取前一关节的公垂线共线的一条公垂线作为 X X X轴;关节轴线相交时, X X X的方向与两周的叉积方向相同。
根据此建模规则,有SDH建模示意图如图1.1所示:

在该坐标系下,各DH参数的含义为:
- a i a_i ai:关节轴线 i − 1 i-1 i−1和关节轴线 i i i的公垂线长度;
- α i \alpha_i αi:关节轴线 i − 1 i-1 i−1和关节轴线 i i i的夹角,指向为从轴线 i − 1 i-1 i−1到轴线 i i i;
- d i d_i di:关节 i i i上的两条公垂线 a i a_i ai与 a i − 1 a_{i-1} ai−1之间的距离,沿关节轴 i i i测量;
- θ i \theta_i θi:连杆 i i i相对于连杆 i − 1 i-1 i−1绕轴线 i i i的旋转角度,绕关节轴线 i − 1 i-1 i−1测量。
根据UR3机器人参数得到其DH参数如表1.1所示:
| 连杆序号 i i i | 连杆长度 a i / m m a_i/mm ai/mm | 连杆扭角 α i / r a d \alpha_i/rad αi/rad | 连杆距离 d i / m m d_i/mm di/mm | 关节转角 θ i / r a d \theta_i/rad θi/rad |
|---|---|---|---|---|
| 1 | 0 0 0 | π / 2 \pi/2 π/2 | 0 0 0 | θ 1 \theta_1 θ1 |
| 2 | 243.65 243.65 243.65 | 0 0 0 | 119.85 119.85 119.85 | θ 2 \theta_2 θ2 |
| 3 | 213 213 213 | 0 0 0 | − 92.85 -92.85 −92.85 | θ 3 \theta_3 θ3 |
| 4 | 0 0 0 | π / 2 \pi/2 π/2 | 83.4 83.4 83.4 | θ 4 \theta_4 θ4 |
| 5 | 0 0 0 | π / 2 \pi/2 π/2 | 83.4 83.4 83.4 | θ 5 \theta_5 θ5 |
| 6 | 0 0 0 | 0 0 0 | 82.4 82.4 82.4 | θ 6 \theta_6 θ6 |
1.1.2 改进型DH法(MDH)建模
改进型DH法建模规则如下:
找原点:找出关节轴 i i i和 i + 1 i+1 i+1之间的公垂线或关节轴 i i i和 i + 1 i+1 i+1的交点,以关节轴 i i i和 i + 1 i+1 i+1的交点或公垂线与关节轴 i i i的交点作为连杆坐标系 i i i的原点;
找 Z Z Z轴: Z i Z_i Zi轴沿关节轴 i i i的指向;
找 X X X轴: X i X_i Xi轴沿公垂线的指向,若关节轴 i i i和 i + 1 i+1 i+1相交,则规定 X i X_i Xi垂直于关节轴 i i i和 i + 1 i+1 i+1所在平面;
确定 Y Y Y轴:按照右手定则确定 Y i Y_i Yi轴。
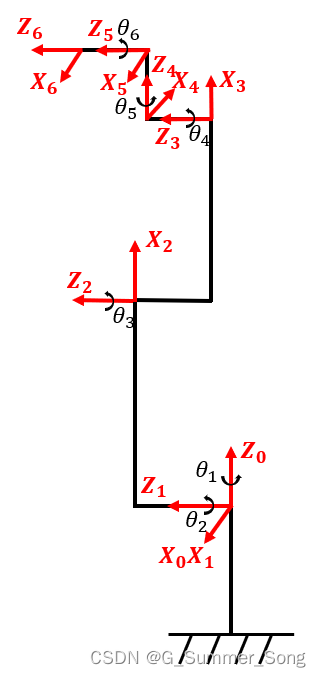
根据此建模规则,有MDH建模示意图如图1.3所示:

使用MDH法建立UR3机器人的连杆坐标系如图1.4所示:

其中各参数的含义如下:
a i − 1 a_{i-1} ai−1:沿 X i − 1 X_{i-1} Xi−1轴,从 Z i − 1 Z_{i-1} Zi−1移动到 Z i Z_i Zi的距离;
α i − 1 \alpha_{i-1} αi−1:沿 X i − 1 X_{i-1} Xi−1轴,从 Z i − 1 Z_{i-1} Zi−1旋转到 Z i Z_i Zi的角度;
d i d_i di:沿 Z i Z_i Zi轴,从 X i − 1 X_{i-1} Xi−1 移动到$ X_i$的距离;
θ i \theta_i θi:沿 Z i Z_i Zi轴,从 X i − 1 X_{i-1} Xi−1旋转到$ X_i$的角度;
根据UR3机器人参数得到其DH参数如表1.2所示:
| 连杆序号 i i i | 连杆长度 a i − 1 / m m a_{i-1}/mm ai−1/mm | 连杆扭角 α i − 1 / r a d \alpha_{i-1}/rad αi−1/rad | 连杆距离 d i / m m d_i/mm di/mm | 关节转角 θ i / r a d \theta_i/rad θi/rad |
|---|---|---|---|---|
| 1 | 0 0 0 | 0 0 0 | 151.9 151.9 151.9 | θ 1 \theta_1 θ1 |
| 2 | 0 0 0 | π / 2 \pi/2 π/2 | 119.85 119.85 119.85 | θ 2 \theta_2 θ2 |
| 3 | − 243.65 -243.65 −243.65 | 0 0 0 | 0 0 0 | θ 3 \theta_3 θ3 |
| 4 | − 213 -213 −213 | 0 0 0 | − 9.45 -9.45 −9.45 | θ 4 \theta_4 θ4 |
| 5 | 0 0 0 | π / 2 \pi/2 π/2 | 83.4 83.4 83.4 | θ 5 \theta_5 θ5 |
| 6 | 0 0 0 | − π / 2 -\pi/2 −π/2 | 82.4 82.4 82.4 | θ 6 \theta_6 θ6 |
1.2 UR3机器人正运动学
根据所建立的坐标系,分别在SDH坐标系以及MDH坐标系下进行正运动学的建模。
1.2.1 SDH坐标系下的正运动学建模
根据SDH坐标系下的连杆关系,有:
T i i − 1 = R o t ( z , θ i ) T r a n s ( z , d i ) T r a n s ( x , a i ) R o t ( x , α i ) \begin{equation} T_{i}^{i-1}=Rot(z,\theta_i)Trans(z,d_i)Trans(x,a_i)Rot(x,\alpha_i) \end{equation} Tii−1=Rot(z,θi)Trans(z,di)Trans(x,ai)Rot(x,αi)
将式(1)右边的四个变换展开可得:
T i i − 1 = [ c θ i − s θ i c α i s θ i s α i a i c θ i s θ i c θ i c α i − c θ i s α i a i s θ i 0 s α i c α i d i 0 0 0 1 ] \begin{align} T_i^{i-1}=\left[ \begin{array}{cccc} c\theta_i & -s\theta_ic\alpha_i & s\theta_is\alpha_i & a_ic\theta_i\\ s\theta_i & c\theta_ic\alpha_i & -c\theta_is\alpha_i & a_is\theta_i\\ 0 & s\alpha_i & c\alpha_i & d_i\\ 0 & 0 & 0 & 1 \end{array} \right] \end{align} Tii−1=⎣⎡cθisθi00−sθicαicθicαisαi0sθisαi−cθisαicαi0aicθiaisθidi1⎦⎤
式中 i = 1 , 2 , 3 , . . . , 6 i=1,2,3,...,6 i=1,2,3,...,6。
为方便表示,定义如下简写:
- c i = c o s θ i c_i=cos\theta_i ci=cosθi
- s i = s i n θ i s_i=sin\theta_i si=sinθi
- c i j = c o s ( θ i + θ j ) c_{ij}=cos(\theta_i+\theta_j) cij=cos(θi+θj)
- s i j = s i n ( θ i + θ j ) s_{ij}=sin(\theta_i+\theta_j) sij=sin(θi+θj)
- c i j k = c o s ( θ i + θ j + θ k ) c_{ijk}=cos(\theta_i+\theta_j+\theta_k) cijk=cos(θi+θj+θk)
- s i j k = s i n ( θ i + θ j + θ k ) s_{ijk}=sin(\theta_i+\theta_j+\theta_k) sijk=sin(θi+θj+θk)
根据表1.1中的DH参数以及式(2)可得各连杆得变换矩阵 T i i − 1 T_i^{i-1} Tii−1,将各连杆的变换矩阵相乘可得机械臂的变矩阵 T 6 0 T^0_6 T60。
{ T 1 0 = [ c 1 0 s 1 0 s 1 0 − c 1 0 0 1 0 d 1 0 0 0 1 ] T 2 1 = [ c 2 − s 2 0 a 2 c 2 s 2 c 2 0 a 2 s 2 0 0 1 d 2 0 0 0 1 ] T 3 2 = [ c 3 − s 3 0 a 3 c 3 s 3 c 3 0 a 3 s 3 0 0 1 d 3 0 0 0 1 ] T 4 3 = [ c 4 0 s 4 0 s 4 0 − c 4 0 0 1 0 d 4 0 0 0 1 ] T 5 4 = [ c 5 0 s 5 0 s 5 0 − c 5 0 0 1 0 d 5 0 0 0 1 ] T 6 5 = [ c 6 − s 6 0 0 s 6 c 6 0 0 0 0 1 d 6 0 0 0 1 ] \begin{cases} T_1^0= \left[\begin{array}{cccc} c_1 & 0 & s_1 & 0\\ s_1 & 0 & -c_1 & 0\\ 0 & 1 & 0 & d_1\\ 0 & 0 & 0 & 1 \end{array}\right]\\ T_2^1= \left[\begin{array}{cccc} c_2 & -s_2 & 0 & a_2c_2\\ s_2 & c_2 & 0 & a_2s_2\\ 0 & 0 & 1 & d_2\\ 0 & 0 & 0 & 1 \end{array}\right]\\ T_3^2= \left[\begin{array}{cccc} c_3 & -s_3 & 0 & a_3c_3\\ s_3 & c_3 & 0 & a_3s_3\\ 0 & 0 & 1 & d_3\\ 0 & 0 & 0 & 1 \end{array}\right]\\ T_4^3= \left[\begin{array}{cccc} c_4 & 0 & s_4 & 0\\ s_4 & 0 & -c_4 & 0\\ 0 & 1 & 0 & d_4\\ 0 & 0 & 0 & 1 \end{array}\right]\\ T_5^4= \left[\begin{array}{cccc} c_5 & 0 & s_5 & 0\\ s_5 & 0 & -c_5 & 0\\ 0 & 1 & 0 & d_5\\ 0 & 0 & 0 & 1 \end{array}\right]\\ T_6^5= \left[\begin{array}{cccc} c_6 & -s_6 & 0 & 0\\ s_6 & c_6 & 0 & 0\\ 0 & 0 & 1 & d_6\\ 0 & 0 & 0 & 1 \end{array}\right]\\ \end{cases} ⎩⎨⎧T10=⎣⎡c1s1000010s1−c10000d11⎦⎤T21=⎣⎡c2s200−s2c2000010a2c2a2s2d21⎦⎤T32=⎣⎡c3s300−s3c3000010a3c3a3s3d31⎦⎤T43=⎣⎡c4s4000010s4−c40000d41⎦⎤T54=⎣⎡c5s5000010s5−c50000d51⎦⎤T65=⎣⎡c6s600−s6c600001000d61⎦⎤
T 6 0 = T 1 0 T 2 1 T 3 2 T 4 3 T 5 4 T 6 5 = [ n x o x a x p x n y o y a y p y n z o z a z p z 0 0 0 1 ] \begin{equation} T_6^0=T_1^0T_2^1T_3^2T_4^3T_5^4T_6^5= \left[ \begin{array}{cccc} n_x & o_x & a_x & p_x\\ n_y & o_y & a_y & p_y\\ n_z & o_z & a_z & p_z\\ 0 & 0 & 0 & 1\\ \end{array} \right] \end{equation} T60=T10T21T32T43T54T65=⎣⎡nxnynz0oxoyoz0axayaz0pxpypz1⎦⎤
式(3)中各简式为:
{ n x = c 6 ( s 1 s 5 + c 1 c 234 c 5 ) + c 1 s 234 s 6 n y = s 1 s 234 s 6 − c 6 ( c 1 s 5 − s 1 c 234 c 5 ) n z = s 234 c 5 c 6 − c 234 s 6 o x = c 1 s 234 c 6 − s 6 ( s 1 s 5 + c 1 c 234 c 5 ) o y = s 6 ( c 1 s 5 − s 1 c 234 c 5 ) + s 1 s 234 c 6 o z = − c 234 c 6 − s 234 c 5 s 6 a x = c 1 c 234 s 5 − s 1 c 5 a y = s 1 c 234 s 5 + c 1 c 5 a z = s 345 s 5 p x = ( c 1 c 234 s 5 − s 1 c 5 ) d 6 + c 1 s 234 d 5 + s 1 d 4 + c 1 c 23 a 3 + s 1 d 3 + c 1 c 2 a 2 + s 1 d 2 p y = ( s 1 c 234 s 5 + c 1 c 5 ) d 6 + s 1 s 234 d 5 − c 1 d 4 + s 1 c 23 a 3 − s 1 d 3 + s 1 c 2 a 2 − c 1 d 2 p z = s 234 s 5 d 6 − c 234 d 5 + s 23 a 3 + s 2 a 2 \begin{cases} n_x = c_6(s_1s_5+c_1c_{234}c_5)+c_1s_{234}s_6\\ n_y = s_1s_{234}s_6-c_6(c_1s_5-s_1c_{234}c_5)\\ n_z = s_{234}c_5c_6-c_{234}s_6\\ o_x = c_1s_{234}c_6-s_6(s_1s_5+c_1c_{234}c_5)\\ o_y = s_6(c_1s_5-s_1c_{234}c_5)+s_1s_{234}c_6\\ o_z = -c_{234}c_6-s_{234}c_5s_6\\ a_x = c_1c_{234}s_5-s_1c_5\\ a_y = s_1c_{234}s_5+c_1c_5\\ a_z = s_{345}s_5\\ p_x = (c_1c_{234}s_5-s_1c_5)d_6+c_1s_{234}d_5+s_1d_4+c_1c_{23}a_3+s_1d_3+c_1c_2a_2+s_1d_2\\ p_y = (s_1c_{234}s_5+c_1c_5)d_6+s_1s_{234}d_5-c_1d_4+s_1c_{23}a_3-s_1d_3+s_1c_2a_2-c_1d_2\\ p_z = s_{234}s_5d_6-c_{234}d_5+s_{23}a_3+s_2a_2 \end{cases} ⎩⎨⎧nx=c6(s1s5+c1c234c5)+c1s234s6ny=s1s234s6−c6(c1s5−s1c234c5)nz=s234c5c6−c234s6ox=c1s234c6−s6(s1s5+c1c234c5)oy=s6(c1s5−s1c234c5)+s1s234c6oz=−c234c6−s234c5s6ax=c1c234s5−s1c5ay=s1c234s5+c1c5az=s345s5px=(c1c234s5−s1c5)d6+c1s234d5+s1d4+c1c23a3+s1d3+c1c2a2+s1d2py=(s1c234s5+c1c5)d6+s1s234d5−c1d4+s1c23a3−s1d3+s1c2a2−c1d2pz=s234s5d6−c234d5+s23a3+s2a2
为了验证模型的正确性,可将其中一个状态代入模型进行检验。对于图1.2中UR3机器人的形态,其对应的关节变量为 Θ = [ 0 π 2 0 π 2 π 0 ] T \Theta=[0\ \frac{\pi}{2}\ 0\ \frac{\pi}{2}\ \pi\ 0]^T Θ=[0 2π 0 2π π 0]T,将其带入式(3)中,得到如下的转换矩阵:
T 6 0 = [ 1 0 0 0 0 0 − 1 − ( d 2 + d 3 + d 4 + d 6 ) 0 1 0 d 4 + a 2 + a 3 0 0 0 1 ] = [ 1 0 0 0 0 0 − 1 − 192.8 0 1 0 540.05 0 0 0 1 ] T_6^0=\left[ \begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & 0 & -1 & -(d_2+d_3+d_4+d_6)\\ 0 & 1 & 0 & d_4+a_2+a_3\\ 0 & 0 & 0 & 1 \end{array} \right]=\left[ \begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & 0 & -1 & -192.8\\ 0 & 1 & 0 & 540.05\\ 0 & 0 & 0 & 1 \end{array} \right] T60=⎣⎡100000100−1000−(d2+d3+d4+d6)d4+a2+a31⎦⎤=⎣⎡100000100−1000−192.8540.051⎦⎤
其中
[ 1 0 0 0 0 − 1 0 1 0 ] \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \\ \end{array} \right] ⎣⎡1000010−10⎦⎤
正好对应{0}系到{6}系的旋转矩阵,并且 [ 0 − 192.8 540.05 ] T \left[0\ -192.8\ 540.05 \right]^T [0 −192.8 540.05]T正好对应{0}系到{6}系平移向量,因此可以初步验证所建立的正运动学模型是正确的。
1.2.2 MDH坐标系下的正运动学建模
根据MDH坐标系下的连杆关系,有:
T i i − 1 = T r a n s ( x , a i − 1 ) R o t ( x , α i − 1 ) T r a n s ( z , d i ) R o t ( z , θ i ) \begin{equation} T_i^{i-1}=Trans(x,a_{i-1})Rot(x,\alpha_{i-1})Trans(z,d_i)Rot(z,\theta_i) \end{equation} Tii−1=Trans(x,ai−1)Rot(x,αi−1)Trans(z,di)Rot(z,θi)
将式(4)右边的四个变换展开可得:
T i i − 1 = [ c θ i − s θ i 0 a i − 1 s θ i c α i − 1 c θ i c α i − 1 − s α i − 1 − d i s α i − 1 s θ i s α i − 1 c θ i s α i − 1 c α i − 1 d i c α i − 1 0 0 0 1 ] \begin{align} T_i^{i-1}=\left[ \begin{array}{cccc} c\theta_i & -s\theta_i & 0 & a_{i-1}\\ s\theta_ic\alpha_{i-1} & c\theta_ic\alpha_{i-1} & -s\alpha_{i-1} & -d_is\alpha_{i-1}\\ s\theta_is\alpha_{i-1} & c\theta_is\alpha_{i-1} & c\alpha_{i-1} & d_ic\alpha_{i-1}\\ 0 & 0 & 0 & 1 \end{array} \right] \end{align} Tii−1=⎣⎡cθisθicαi−1sθisαi−10−sθicθicαi−1cθisαi−100−sαi−1cαi−10ai−1−disαi−1dicαi−11⎦⎤
式中 i = 1 , 2 , 3 , . . . , 6 i=1,2,3,...,6 i=1,2,3,...,6
根据表1.2中的DH参数以及式(5)可得各连杆得变换矩阵 T i i − 1 T_i^{i-1} Tii−1,将各连杆的变换矩阵相乘可得机械臂的变矩阵 T 6 0 T^0_6 T60。
{ T 1 0 = [ c 1 − s 1 0 0 s 1 c 1 0 0 0 0 1 d 1 0 0 0 1 ] T 2 1 = [ c 2 − s 2 0 0 0 0 − 1 − d 2 s 2 c 2 0 0 0 0 0 1 ] T 3 2 = [ c 3 − s 3 0 a 2 s 3 c 3 0 0 0 0 1 0 0 0 0 1 ] T 4 3 = [ c 4 − s 4 0 a 3 s 4 c 4 0 0 0 0 1 d 4 0 0 0 1 ] T 5 4 = [ c 5 − s 5 0 0 0 0 − 1 − d 5 s 5 c 5 0 0 0 0 0 1 ] T 6 5 = [ c 6 − s 6 0 0 0 0 1 d 6 − s 6 − c 6 0 0 0 0 0 1 ] \begin{cases} T_1^0= \left[\begin{array}{cccc} c_1 & -s_1 & 0 & 0\\ s_1 & c_1 & 0 & 0\\ 0 & 0 & 1 & d_1\\ 0 & 0 & 0 & 1 \end{array}\right]\\ T_2^1= \left[\begin{array}{cccc} c_2 & -s_2 & 0 & 0\\ 0 & 0 & -1 & -d_2\\ s_2 & c_2 & 0 & 0\\ 0 & 0 & 0 & 1 \end{array}\right]\\ T_3^2= \left[\begin{array}{cccc} c_3 & -s_3 & 0 & a_2\\ s_3 & c_3 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{array}\right]\\ T_4^3= \left[\begin{array}{cccc} c_4 & -s_4 & 0 & a_3\\ s_4 & c_4 & 0 & 0\\ 0 & 0 & 1 & d_4\\ 0 & 0 & 0 & 1 \end{array}\right]\\ T_5^4= \left[\begin{array}{cccc} c_5 & -s_5 & 0 & 0\\ 0 & 0 & -1 & -d_5\\ s_5 & c_5 & 0 & 0\\ 0 & 0 & 0 & 1 \end{array}\right]\\ T_6^5= \left[\begin{array}{cccc} c_6 & -s_6 & 0 & 0\\ 0 & 0 & 1 & d_6\\ -s_6 & -c_6 & 0 & 0\\ 0 & 0 & 0 & 1 \end{array}\right] \end{cases} ⎩⎨⎧T10=⎣⎡c1s100−s1c100001000d11⎦⎤T21=⎣⎡c20s20−s20c200−1000−d201⎦⎤T32=⎣⎡c3s300−s3c3000010a2001⎦⎤T43=⎣⎡c4s400−s4c4000010a30d41⎦⎤T54=⎣⎡c50s50−s50c500−1000−d501⎦⎤T65=⎣⎡c60−s60−s60−c6001000d601⎦⎤
T 6 0 = T 1 0 T 2 1 T 3 2 T 4 3 T 5 4 T 6 5 = [ n x o x a x p x n y o y a y p y n z o z a z p z 0 0 0 1 ] \begin{equation} T_6^0=T_1^0T_2^1T_3^2T_4^3T_5^4T_6^5= \left[ \begin{array}{cccc} n_x & o_x & a_x & p_x\\ n_y & o_y & a_y & p_y\\ n_z & o_z & a_z & p_z\\ 0 & 0 & 0 & 1\\ \end{array} \right] \end{equation} T60=T10T21T32T43T54T65=⎣⎡nxnynz0oxoyoz0axayaz0pxpypz1⎦⎤
式(6)中各简式如下:
{ n x = c 6 ( s 1 s 5 + c 1 c 234 c 5 ) − c 1 s 234 s 6 n y = − c 6 ( c 1 s 5 − s 1 c 234 c 5 ) − s 1 s 234 s 6 n z = c 234 s 6 + s 234 c 5 c 6 o x = − s 6 ( s 1 s 5 + c 1 c 234 c 5 ) − c 1 s 234 c 6 o y = s 6 ( c 1 s 5 − s 1 c 234 c 5 ) − s 1 s 234 c 6 o z = c 234 c 6 − s 234 c 5 s 6 a x = s 1 c 5 − c 1 c 234 s 5 a y = − c 1 c 5 − s 1 c 234 s 5 a z = − s 234 s 5 p x = ( s 1 c 5 − c 1 c 234 s 5 ) d 6 + c 1 s 234 d 5 + c 1 c 23 a 3 + s 1 d 4 + c 1 c 2 a 2 + s 1 d 2 p y = − ( c 1 c 5 + s 1 c 234 s 5 ) d 6 + s 1 s 234 d 5 + s 1 c 23 a 3 − c 1 d 4 + s 1 c 2 a 2 − c 1 d 2 p z = − s 234 s 5 d 6 − c 234 d 5 + s 23 a 3 + s 2 a 2 + d 1 \begin{cases} n_x = c_6(s_1s_5+c_1c_{234}c_5)-c_1s_{234}s_6\\ n_y = -c_6(c_1s_5-s_1c_{234}c_5)-s_1s_{234}s_6\\ n_z = c_{234}s_6+s_{234}c_5c_6\\ o_x = -s_6(s_1s_5+c_1c_{234}c_5)-c_1s_{234}c_6\\ o_y = s_6(c_1s_5-s_1c_{234}c_5)-s_1s_{234}c_6\\ o_z = c_{234}c_6-s_{234}c_5s_6\\ a_x = s_1c_5-c_1c_{234}s_5\\ a_y = -c_1c_5-s_1c_{234}s_5\\ a_z = -s_{234}s_5\\ p_x = (s_1c_5-c_1c_{234}s_5)d_6+c_1s_{234}d_5+c_1c_{23}a_3+s_1d_4+c_1c_2a_2+s_1d_2\\ p_y = -(c_1c_5+s_1c_{234}s_5)d_6+s_1s_{234}d_5+s_1c_{23}a_3-c_1d_4+s_1c_2a_2-c_1d_2\\ p_z = -s_{234}s_5d_6-c_{234}d_5+s_{23}a_3+s_2a_2+d_1 \end{cases} ⎩⎨⎧nx=c6(s1s5+c1c234c5)−c1s234s6ny=−c6(c1s5−s1c234c5)−s1s234s6nz=c234s6+s234c5c6ox=−s6(s1s5+c1c234c5)−c1s234c6oy=s6(c1s5−s1c234c5)−s1s234c6oz=c234c6−s234c5s6ax=s1c5−c1c234s5ay=−c1c5−s1c234s5az=−s234s5px=(s1c5−c1c234s5)d6+c1s234d5+c1c23a3+s1d4+c1c2a2+s1d2py=−(c1c5+s1c234s5)d6+s1s234d5+s1c23a3−c1d4+s1c2a2−c1d2pz=−s234s5d6−c234d5+s23a3+s2a2+d1
为了验证模型的正确性,可将其中一个状态代入模型进行检验。对于图1.4中UR3机器人的形态,其对应的关节变量为 Θ = [ 0 − π 2 0 − π 2 0 0 ] T \Theta=[0\ -\frac{\pi}{2}\ 0\ -\frac{\pi}{2}\ 0\ 0]^T Θ=[0 −2π 0 −2π 0 0]T,将其带入式(6)中,得到如下的转换矩阵:
T 6 0 = [ − 1 0 0 0 0 0 − 1 − ( d 6 + d 4 + d 2 ) 0 − 1 0 d 1 + d 5 − a 2 − a 3 0 0 0 1 ] = [ − 1 0 0 0 0 0 − 1 − 192.8 0 − 1 0 691.95 0 0 0 1 ] T_6^0=\left[ \begin{array}{cccc} -1 & 0 & 0 & 0\\ 0 & 0 & -1 & -(d_6+d_4+d_2)\\ 0 & -1 & 0 & d_1+d_5-a_2-a_3\\ 0 & 0 & 0 & 1 \end{array} \right]=\left[ \begin{array}{cccc} -1 & 0 & 0 & 0\\ 0 & 0 & -1 & -192.8\\ 0 & -1 & 0 & 691.95\\ 0 & 0 & 0 & 1 \end{array} \right] T60=⎣⎡−100000−100−1000−(d6+d4+d2)d1+d5−a2−a31⎦⎤=⎣⎡−100000−100−1000−192.8691.951⎦⎤
其中
[ − 1 0 0 0 0 − 1 0 − 1 0 ] \left[ \begin{array}{ccc} -1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & -1 & 0 \\ \end{array} \right] ⎣⎡−10000−10−10⎦⎤
正好对应{0}系到{6}系的旋转矩阵,并且 [ 0 − 192.8 691.95 ] T \left[0\ -192.8\ 691.95 \right]^T [0 −192.8 691.95]T正好对应{0}系到{6}系平移向量,因此可以初步验证所建立的正运动学模型是正确的。后文中将通过仿真来进一步验证模型的正确性。
由于在不同的坐标系下DH参数的含义有所不同,推导出来的正运动学模型也会有所差别。在后文的分析中,若无特别说明,将使用MDH坐标系下推导出来的正运动学模型。
边栏推荐
- JS写一段代码,判断一个字符串中出现次数最多的字符串,并统计出现的次数JS
- Cholesterol-PEG-Amine CLS-PEG-NH2 Cholesterol-Polyethylene Glycol-Amino Research Use
- 活体检测PatchNet学习笔记
- Numpy常用函数
- DSPE-PEG-COOH CAS: 1403744-37-5 Phospholipid-polyethylene glycol-carboxy lipid PEG conjugate
- MySQL 主从切换步骤
- mPEG-DMPE Methoxy-polyethylene glycol-bismyristyl phosphatidylethanolamine for stealth liposome formation
- The content of the wangeditor editor is transferred to the background server for storage
- TransactionTemplate transaction programmatic way
- Cholesterol-PEG-Acid CLS-PEG-COOH Cholesterol-Polyethylene Glycol-Carboxyl Modified Peptides
猜你喜欢
Pytorch常用函数

The solution to the IDEA console not being able to enter information
Multi-Modal Face Anti-Spoofing Based on Central Difference Networks学习笔记

Attention based ASR(LAS)
2022年SQL大厂高频实战面试题(详细解析)

softmax函数详解

二进制转换成十六进制、位运算、结构体

Cholesterol-PEG-NHS NHS-PEG-CLS cholesterol-polyethylene glycol-active ester can modify small molecular materials
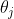
人脸识别AdaFace学习笔记
活体检测CDCN学习笔记
随机推荐
Remote file xxx is mapped to the local path xxx and can‘t be found. You can continue debugging....
Pytorch常用函数
ImportError: cannot import name ‘Xxxx‘ from partially initialized module ‘xx.xx.xx‘
Data Preprocessing, Feature Engineering, and Feature Learning - Excerpt
超参数优化-摘抄
mPEG-DSPE 178744-28-0 甲氧基-聚乙二醇-磷脂酰乙醇胺线性PEG磷脂
Picture-in-Picture API in the browser
Cholesterol-PEG-DBCO 胆固醇-聚乙二醇-二苯基环辛炔化学试剂
数据预处理、特征工程和特征学习-摘抄
Podspec verification dependency error problem pod lib lint , need to specify the source
Jupyter内核正忙、内核挂掉
Tensorflow边用边踩坑
自己设置的私密文件,在哪找
The solution to the IDEA console not being able to enter information
使用 OpenCV 提取图像的 HOG、SURF 及 LBP 特征 (含代码)
Evaluating Machine Learning Models - Excerpt
OpenCV中的图像数据格式CV_8U定义
【Rhapsody学习笔记】3:Dishwasher
Wangeditor rich text editor to upload pictures and solve cross-domain problems
Pytorch实现ResNet