当前位置:网站首页>poj 2762 Going from u to v or from v to u? (推断它是否是一个薄弱环节图)
poj 2762 Going from u to v or from v to u? (推断它是否是一个薄弱环节图)
2022-07-05 23:01:00 【全栈程序员站长】
大家好,又见面了,我是全栈君
意甲冠军:给定一个有向图有m单向边缘。免费推断是否两点起来(a可以b要么b可以a或最多彼此),该请求
弱联通重量。
算法:
缩点求强连通分量。然后又一次建图。推断新图是否是一条单链,即不能分叉,假设分叉了就会存在不可达的情况。
怎么推断是否是单链呢?
就是每次入度为0的点都仅仅有一个,即每次队列里仅仅有一个点。
( o(╯□╰)o。。。。
。好像已经是第二次用pair记录原图的点对,然后存pair的vector忘记清空导致wa来wa去!
)
#include<cstdio>
#include<iostream>
#include<cstring>
#include<queue>
#include<vector>
#define maxn 1010
#define maxm 20010
using namespace std;
struct node
{
int to,next;
}edge[maxm],edge2[maxm];
int head[maxn],cnt,n;
int clk,top,s[maxn],scc,dfn[maxn],low[maxn],belong[maxn];
bool instack[maxn],vis[maxn];
int head2[maxn],cnt2,in[maxn];
typedef pair<int,int> PII;
vector<PII> xx;
queue<int> q;
void add(int x,int y)
{
edge[cnt].to = y;
edge[cnt].next = head[x];
head[x] = cnt++;
}
void add2(int x,int y)
{
edge2[cnt2].to = y;
edge2[cnt2].next = head2[x];
head2[x] = cnt2++;
}
void dfs(int x)
{
dfn[x] = low[x] = clk++;
s[top++] = x;
instack[x] = true;
for(int i=head[x];i!=-1;i = edge[i].next)
{
int u = edge[i].to;
if(dfn[u]==-1)
{
dfs(u);
low[x] = min(low[u],low[x]);
}
else if(instack[u])
{
low[x] = min(low[x],dfn[u]);
}
}
if(low[x]==dfn[x])
{
int u;
scc++;
do
{
u = s[--top];
instack[u]=false;
belong[u] = scc;
}while(u!=x);
}
}
void tarjan()
{
memset(dfn,-1,sizeof(dfn));
memset(instack,0,sizeof(instack));
memset(belong,0,sizeof(belong));
clk = top = scc = 0;
for(int i=1;i<=n;i++)
{
if(dfn[i]==-1)
dfs(i);
}
}
bool topo()
{
memset(vis,0,sizeof(vis));
int c = 0;
while(!q.empty())
q.pop();
for(int i=1;i<=scc;i++)
{
if(!in[i])
{
c++;
q.push(i);
}
}
if(c>1) return false;
while(!q.empty())
{
int u = q.front();
q.pop();
if(vis[u]) continue;
vis[u] = true;
c = 0;
for(int i=head2[u];i!=-1;i=edge2[i].next)
{
int v = edge2[i].to;
in[v]--;
if(!in[v])
{
q.push(v);
c++;
}
}
if(c>1)
return false;
}
return true;
}
int main()
{
int m,a,b,T;
scanf("%d",&T);
while(T--)
{
scanf("%d%d",&n,&m);
memset(head,-1,sizeof(head));
memset(in,0,sizeof(in));
xx.clear();
cnt = 0;
for(int i=1;i<=m;i++)
{
scanf("%d%d",&a,&b);
add(a,b);
xx.push_back(make_pair(a,b));
}
tarjan();
memset(head2,-1,sizeof(head2));
cnt2 = 0;
for(int i=0;i<xx.size();i++)
{
int u = xx[i].first,v = xx[i].second;
if(belong[u]!=belong[v])
{
add2(belong[u],belong[v]);
in[belong[v]]++;
}
}
if(topo()) printf("Yes\n");
else printf("No\n");
}
return 0;
}版权声明:本文博客原创文章,博客,未经同意,不得转载。
发布者:全栈程序员栈长,转载请注明出处:https://javaforall.cn/117526.html原文链接:https://javaforall.cn
边栏推荐
- 判斷二叉樹是否為完全二叉樹
- February 13, 2022 -5- maximum depth of binary tree
- Global and Chinese market of networked refrigerators 2022-2028: Research Report on technology, participants, trends, market size and share
- Roman numeral to integer
- Douban scoring applet Part-2
- 秒杀系统的设计与实现思路
- Multi sensor fusion of imu/ electronic compass / wheel encoder (Kalman filter)
- 数学公式截图识别神器Mathpix无限使用教程
- 一文搞定class的微觀結構和指令
- Leetcode daily question 1189 The maximum number of "balloons" simple simulation questions~
猜你喜欢
Week 17 homework

How to quickly understand complex businesses and systematically think about problems?
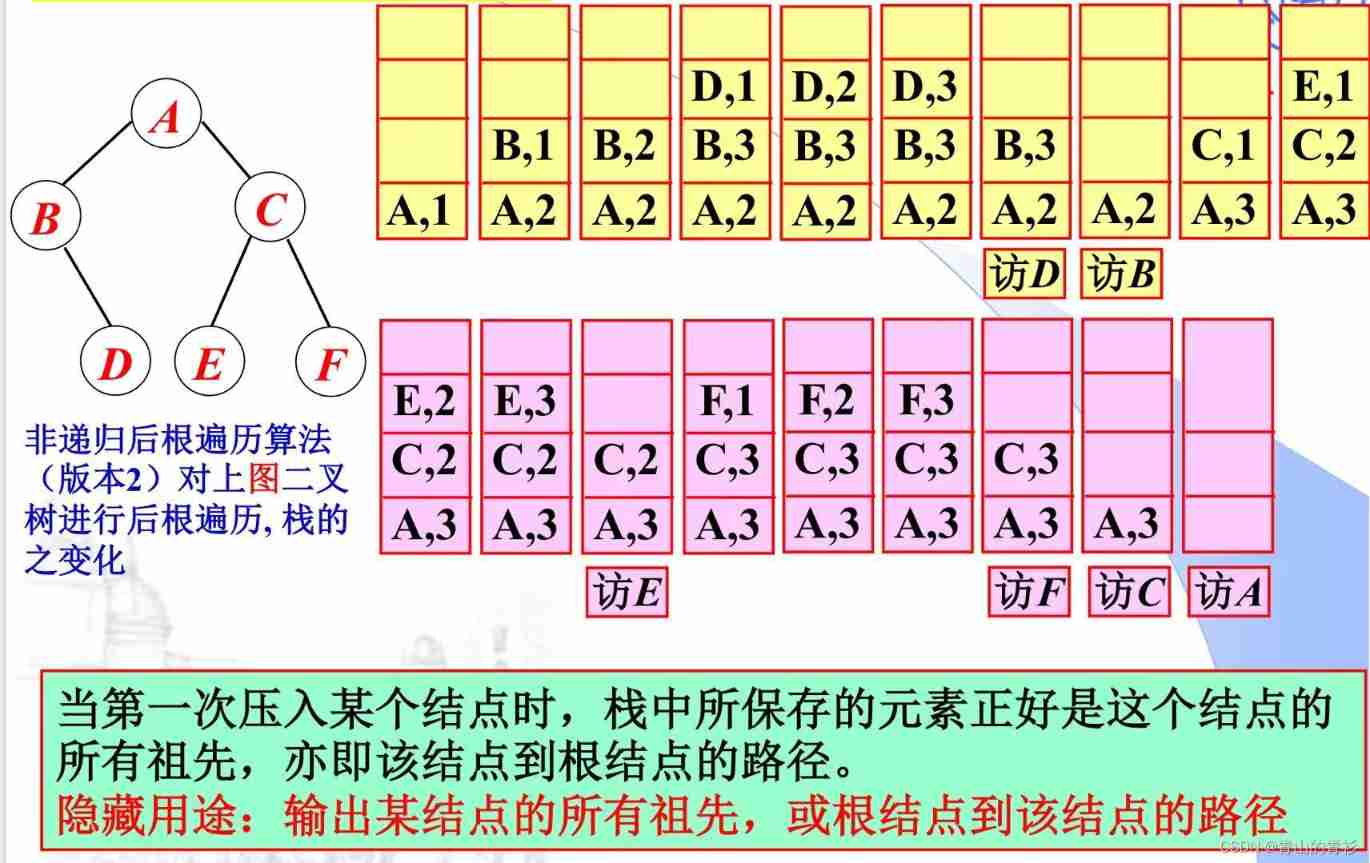
LeetCode145. Post order traversal of binary tree (three methods of recursion and iteration)
d3dx9_ How to repair 31.dll_ d3dx9_ 31. Solution to missing DLL
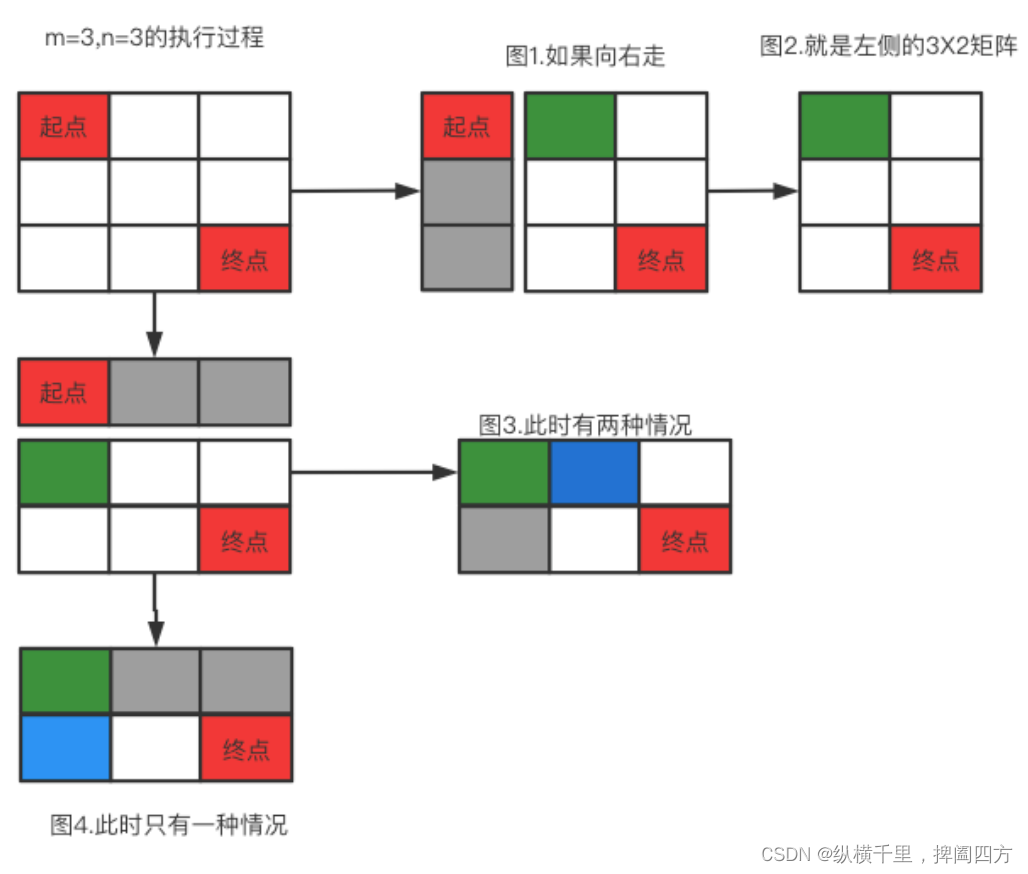
Finally understand what dynamic planning is
查看网页最后修改时间方法以及原理简介
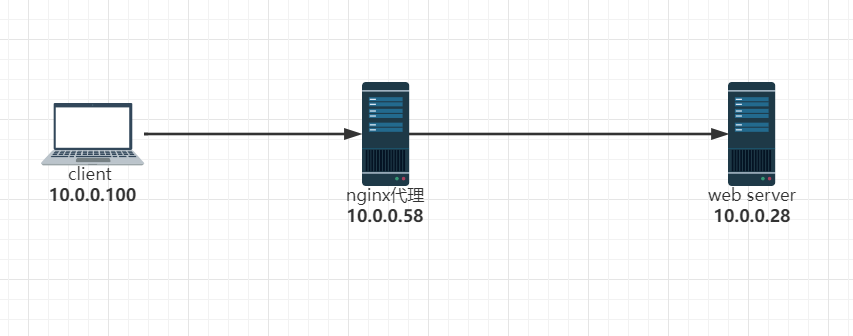
实现反向代理客户端IP透传

Hainan Nuanshen tea recruits warmhearted people: recruitment of the product experience recommender of Nuanshen multi bubble honey orchid single cluster

【Note17】PECI(Platform Environment Control Interface)
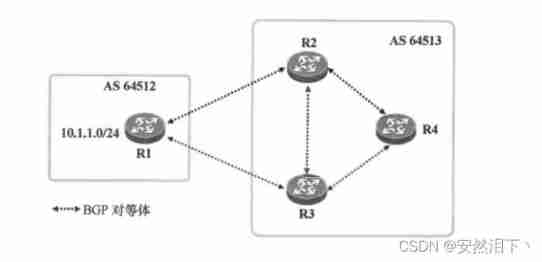
Hcip day 12 (BGP black hole, anti ring, configuration)
随机推荐
Nacos installation and service registration
Element positioning of Web Automation
d3dx9_ How to repair 31.dll_ d3dx9_ 31. Solution to missing DLL
C Primer Plus Chapter 9 question 10 binary conversion
并查集实践
Global and Chinese market of networked refrigerators 2022-2028: Research Report on technology, participants, trends, market size and share
Negative sampling
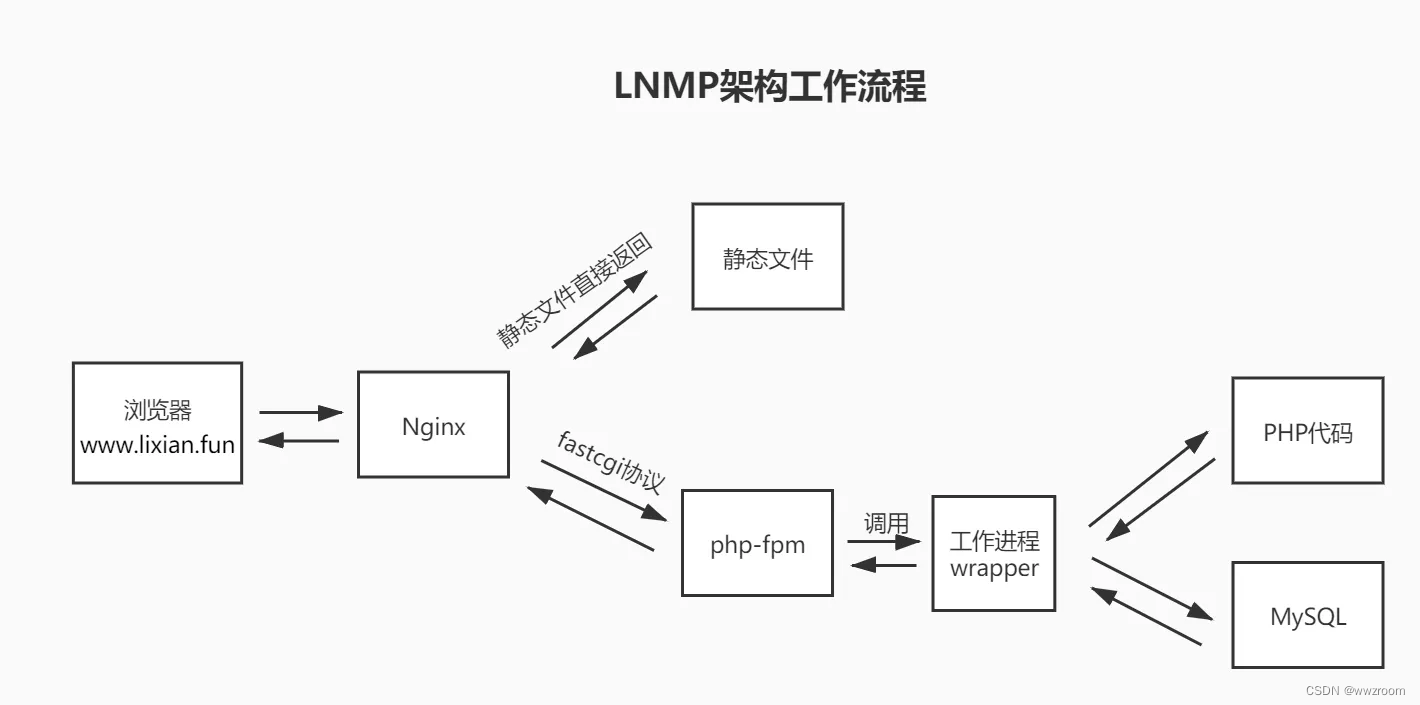
利用LNMP实现wordpress站点搭建
Using LNMP to build WordPress sites
Use of grpc interceptor
【原创】程序员团队管理的核心是什么?
【Note17】PECI(Platform Environment Control Interface)
视频标准二三事
fibonacci search
Calculating the number of daffodils in C language
Activate function and its gradient
Summary of binary tree recursive routines
(4)UART應用設計及仿真驗證2 —— TX模塊設計(無狀態機)
2.13 summary
3 find the greatest common divisor and the least common multiple