当前位置:网站首页>【第29天】给定一个整数,请你求出它的因子数
【第29天】给定一个整数,请你求出它的因子数
2022-07-03 00:51:00 【执 梗】
序、专栏前言
本专栏开启,目的在于帮助大家更好的掌握学习Java,特别是一些Java学习者难以在网上找到系统地算法学习资料帮助自身入门算法,同时对于专栏内的内容有任何疑问都可在文章末尾添加我的微信给你进行一对一的讲解。
但最最主要的还是需要独立思考,对于本专栏的所有内容,能够进行完全掌握,自己完完全全将代码写过一遍,对于算法入门肯定是没有问题的。
算法的学习肯定不能缺少总结,这里我推荐大家可以到高校算法社区将学过的知识进行打卡,以此来进行巩固以及复习。
学好算法的唯一途径那一定是题海战略,大量练习的堆积才能练就一身本领。专栏的任何题目我将会从【题目描述】【解题思路】【模板代码】【代码解析】等四板块进行讲解。
一、【例题1】
1、题目描述
给定一个整数 n ( 1 ≤ n ≤ 100000 ) n(1\le n \le100000) n(1≤n≤100000),请你求出它的因子数量。
2、解题思路
- ( 1 ) (1) (1)我们可以联想到之前判断质数的文章,因为质数的判定也是看一个数的因子数,那时就已经写出了 O ( n ) O(n) O(n)和一个 O ( n ) O(\sqrt n) O(n)的做法。
3、模板代码
1.O(n)做法
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int ans=0;
for (int i = 1; i <=n; i++) {
if (n%i==0) ans++;
}
System.out.println(ans);
}
}
2.根号n做法
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int ans=0;
for (int i = 1; i <=n/i; i++) {
if (n%i==0){
if (i!=n/i) ans+=2;
else ans++;
}
}
System.out.println(ans);
}
}
3.约数个数定理
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
System.out.println(getsum(n));
}
static int getsum(int n){
int ans=1;
for (int i = 2; i <=n/i; i++) {
if (n%i==0){
int a=0;
while (n%i==0){
a++;
n/=i;
}
ans*=(a+1);
}
}
if (n>1) ans*=2;
return ans;
}
}
4、代码解析
- ( 1 ) (1) (1)前两种方法在这不讲,在第 5 5 5天的质数判定中讲解过,重点讲一下约数个数定理。
- ( 2 ) (2) (2)对于一个大于 1 1 1的整数 n n n,可以分解质因数
n = ∏ i = 1 k p i a i = p 1 a 1 × p 2 a 2 × p 3 a 3 . . . . . . p k a k n=\prod_{i=1}^{k} p_i^{a^i}=p_1^{a^1}\times p_2^{a^2}\times p_3^{a^3}......p_k^{a^k} n=i=1∏kpiai=p1a1×p2a2×p3a3......pkak
则 n n n的正约数个数为 f ( n ) = ∏ i = 1 k ( a i + 1 ) = ( a 1 + 1 ) ( a 2 + 1 ) . . . ( a k + 1 ) 。 f(n)=\prod_{i=1}^{k}(a_i+1)=(a_1+1)(a_2+1)...(a_k+1)。 f(n)=∏i=1k(ai+1)=(a1+1)(a2+1)...(ak+1)。
其中 a 1 、 a 2 、 a 3 . . . a k a_1、a_2、a_3...a_k a1、a2、a3...ak是 p 1 、 p 2 、 p 3 、 . . . p k p_1、p_2、p_3、...p_k p1、p2、p3、...pk的指数。 - ( 3 ) (3) (3)定理证明:对于 n n n,我们有: n = p 1 a 1 × p 2 a 2 × p 3 a 3 . . . . . . p k a k n=p_1^{a^1}\times p_2^{a^2}\times p_3^{a^3}......p_k^{a^k} n=p1a1×p2a2×p3a3......pkak
对于 n n n的任意一个约数 d d d,则有 d = p 1 β 1 × p 2 β 2 × p 3 β 3 . . . . . . p k β k d=p_1^{^\beta1}\times p_2^{\beta ^2}\times p_3^{\beta ^3}......p_k^{\beta^k} d=p1β1×p2β2×p3β3......pkβk,其中 ( 0 ≤ β i ≤ a i ) (0 \le \beta_i \leq a_i) (0≤βi≤ai),每一个 β i \beta_i βi的取值总共有 ( a i + 1 ) 个 (a_i+1)个 (ai+1)个。每一项的 β i \beta _i βi不同,则约数就不相同。 β 1 \beta _1 β1的范围是 [ 0 , a 1 ] [0,a_1] [0,a1], β 2 \beta _2 β2的范围是 [ 0 , a i ] [0,a_i] [0,ai], β k \beta _k βk的去取值范围是 [ 0 , a k ] [0,a_k] [0,ak]。 - ( 4 ) (4) (4)根据乘法原理, n n n的约数个数 f ( n ) = ( a 1 + 1 ) ( a 2 + 1 ) . . . ( a k + 1 ) f(n)=(a_1+1)(a_2+1)...(a_k+1) f(n)=(a1+1)(a2+1)...(ak+1)

三、推荐专栏
四、课后习题
| 序号 | 题目链接 | 难度评级 |
|---|---|---|
| 1 | 丑数 | 2 |
边栏推荐
猜你喜欢
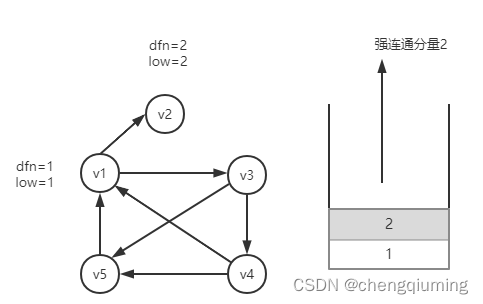
有向图的强连通分量
![[AUTOSAR I overview]](/img/e4/b97c6beebf6f431d2d7cf209c6683e.png)
[AUTOSAR I overview]

数据分析思维分析犯法和业务知识——分析方法(一)
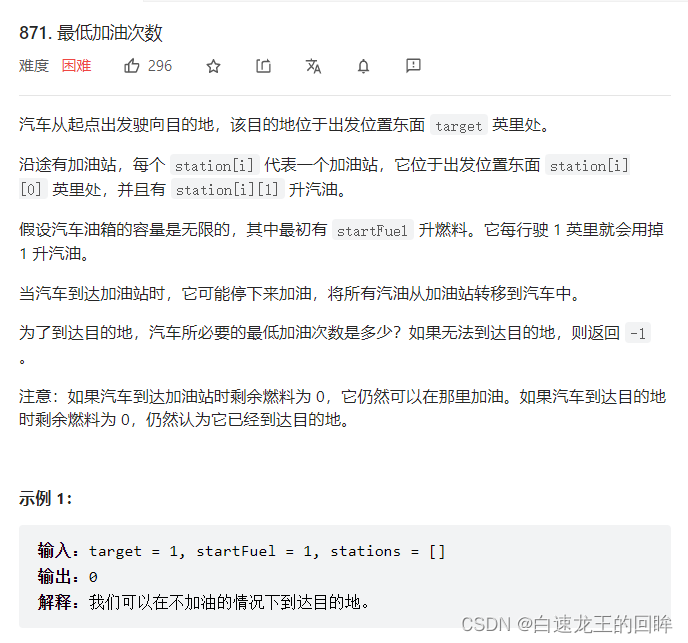
leetcode:871. 最低加油次数【以前pat做过 + 最大堆 +贪心】
Asynchronous, email and scheduled tasks

攻克哈希的基本概念与实现
![[AUTOSAR VI description document]](/img/3d/1382acbc4054ab218485a12b7b4e6b.png)
[AUTOSAR VI description document]

飞凌搭载TI AM62x的ARM核心板/开发板首发上市,亮相Embedded World 2022
Win10 can't be installed in many ways Problems with NET3.5

Machine learning terminology
随机推荐
链表中的节点每k个一组翻转
matlab查找某一行或者某一列在矩阵中的位置
1038 Recover the Smallest Number
Key detection and sinusoidal signal output developed by Arduino
Basic concept and implementation of overcoming hash
Asynchronous, email and scheduled tasks
1696C. Fishingprince Plays With Array【思维题 + 中间状态 + 优化存储】
R language generalized linear model function GLM, (model fit and expression diagnostics), model adequacy evaluation method, use plot function and car package function
Daily topic: movement of haystack
R language ggplot2 visual faceting, visual facet_wrap bar plot, using strip Text function customize the size of the strip of each facet title in the facet graph (cutimi
安全运营四要素之资产、脆弱性、威胁和事件
合并K个已排序的链表
Kivy教程大全之如何在 Kivy 中创建下拉列表
[case sharing] let the development of education in the new era advance with "number"
Delete duplicate elements in the ordered linked list -ii
Understanding and distinguishing of some noun concepts in adjustment / filtering
MySQL
每日一题之干草堆的移动
Solve the cache problem of reactnative using WebView
Find a benchmark comrade in arms | a million level real-time data platform, which can be used for free for life