当前位置：网站首页>二叉树常见的问题和解决思路
二叉树常见的问题和解决思路
2022-08-03 05:23:00 【圆月弯刀鞘】
文章目录
〇、整体思路
树的结构决定了关于树的操作大多可以使用递归的思想进行实现，很多问题的解决都融合了前序、中序和后序遍历。
常见的递归出口有：判断节点是否为空
一、判断是否为AVL
判断二叉树是否为平衡树可以借助递归思想，在递的过程中计算节点的深度，在归的时候返回节点的平衡因子，以此来判断树是否平衡。
代码示例如下：
//重载的递归函数
int is_AVL(const Node *root, int level, bool &flag) {
if (root == nullptr || !flag) {
return level + 1;
}
int level_of_left = is_AVL(root->_left, level + 1, flag);
int level_of_right = is_AVL(root->_right, level + 1, flag);
if (abs(level_of_left - level_of_right) > 1) {
flag = false;
}
return max(level_of_right, level_of_left);
}
//主函数
bool is_AVL(const Node *root) {
bool flag = true;
is_AVL(root, 0, flag);
return flag;
}
二、判断是否对称
借助递归的思想，从根节点开始，将指针分成两路，一路向左走，一路向右走。递归的出口是遇到了空节点或者两个指针指向的节点元素不相同。
//重载的递归函数
bool is_symmetric(Node *cur1, Node *cur2) {
if (cur1 == nullptr && cur2 == nullptr) {
return true;
}
if (cur1 == nullptr || cur2 == nullptr) {
return false;
}
if (cur1->_val != cur2->_val) {
return false;
}
return is_symmetric(cur1->_left, cur2->_right) && is_symmetric(cur1->_right, cur2->_left);
}
//主函数
bool is_symmetric(Node* root) {
if (root == nullptr) {
return true;
}
return is_symmetric(_root->_left, _root->_right);
}
三、判断是否为BST
借助中序遍历是有序的思想，遍历二叉树，判断前一个访问的节点和当前节点的大小关系，判断二叉树是否为BST
//重载的递归函数
bool judge_BST(Node *root, Node *&pre) {
if (root == nullptr) {
return true;
}
if (!is_BST(root->_left, pre)) {
return false;
}
if (pre != nullptr) {
if (root->_val < pre->_val) {
return false;
}
}
pre = root;
is_BST(root->_right, pre);
}
//主函数
bool is_BST(Node* root) {
Node *pre = nullptr;
return is_BST(root, pre);
}
四、各种遍历
利用递归的思想可以很方便的进行遍历。
//前序遍历
void pre_order(Node *root) {
if (root == nullptr) {
return;
}
cout << root->_val << " ";
pre_order(root->_left);
pre_order(root->_right);
}
//中序遍历
void in_order(Node *root) {
if (root == nullptr) {
return;
}
in_order(root->_left);
cout << root->_val << " ";
in_order(root->_right);
}
//后序遍历
void post_order(Node *root) {
Node *cur = root;
if (cur == nullptr) {
return;
}
post_order(cur->_left);
post_order(cur->_right);
cout << cur->_val << endl;
}
非递归的前中后遍历可以借助stack进行实现，层次遍历借助queue实现
//前序遍历
void pre_order(Node* root) {
if (root == nullptr) {
return;
}
stack<Node *> s;
s.push(root);
Node *right;
Node *left;
while (!s.empty()) {
cout << s.top()->_val << endl;
right = s.top()->_right;
left = s.top()->_left;
s.pop();
if (right != nullptr) {
s.push(right);
}
if (left != nullptr) {
s.push(left);
}
}
}
//中序遍历，先从根节点一路向左将节点入栈，然后开始访问栈顶并出栈，
//出栈的元素如果有右节点，将其入栈，然后再一路向左，知道栈空
void in_order(Node* root) {
if (root == nullptr) {
return;
}
Node *cur = root;
stack<Node *> s;
s.push(cur);
while (cur->_left != nullptr) {
cur = cur->_left;
s.push(cur);
}
while (!s.empty()) {
cout << s.top()->_val << endl;
cur = s.top();
s.pop();
if (cur->_right != nullptr) {
cur = cur->_right;
s.push(cur);
}
while (cur->_left != nullptr) {
cur = cur->_left;
s.push(cur);
}
}
}
//后序遍历，相对复杂，借助两个栈实现，先用一个栈实现VRL遍历，
//然后用另外一个栈进行逆序
void post_order(Node* root) {
if (root == nullptr) {
return;
}
stack<Node *> s1;
stack<Node *> s2;
Node *cur = root;
s1.push(cur);
while (!s1.empty()) {
cur = s1.top();
s2.push(cur);
s1.pop();
if (cur->_left != nullptr) {
s1.push(cur->_left);
}
if (cur->_right != nullptr) {
s1.push(cur->_right);
}
}
while (!s2.empty()) {
cout << s2.top()->_val << endl;
s2.pop();
}
}
五、将二叉树进行中心对称反转
中心对称反转，从根节点开始，使用递归的思想，反转左孩子和右孩子，遇到空节点的时候返回。
//主函数
void mirror_transfer() {
mirror_transfer(root);
}
//重载递归函数
void mirror_transfer(Node *root) {
if (root == nullptr) {
return;
}
Node *tmp = root->_left;
root->_left = root->_right;
root->_right = tmp;
mirror_transfer(root->_left);
mirror_transfer(root->_right);
}
六、求某种遍历顺序中的倒数第k个节点
可以使用遍历的思想将某种遍历次序进行反转，求其正数第k个节点。
七、求二叉树的节点个数
使用递归的思想，逐层计算，递归出口为空节点
//主函数
int get_node_numbers() {
return get_node_numbers(_root);
}
//重载的递归函数
int get_node_numbers(Node *root) {
if (root == nullptr) {
return 0;
}
return get_node_numbers(root->_left) + get_node_numbers(root->_right) + 1;
}
八、求二叉树的层数
利用递归的思想分别求左子树和右子树的层数。
//主函数
int get_level_numbers() {
return get_level_numbers(_root);
}
//重载的递归函数
int get_level_numbers(Node *root) {
if (root == nullptr) {
return 0;
}
return max(get_level_numbers(root->_left), get_level_numbers(root->_right)) + 1;
}
九、搜索BST中指定区间的元素
利用BST的根节点大于所有左子树节点，并小于所有右子树节点的性质进行节点遍历和判断。
//主函数
void search_between(int val1, int val2) {
search_between(_root, val1, val2);
}
//重载的递归函数
void search_between(Node *root, int val1, int val2) {
if (root == nullptr) {
return;
}
if (root->_val >= val1 && root->_val <= val2) {
cout << root->_val << endl;
search_between(root->_left, val1, val2);
search_between(root->_right, val1, val2);
} else if (val1 > root->_val) {
search_between(root->_right, val1, val2);
} else {
search_between(root->_left, val1, val2);
}
}
十、求两个节点的最近公共祖先节点(LCA)
利用递归的思想，从根节点开始，如果当前的节点比两个节点都大，就在左子树中寻找LCA，如果当前节点比两个节点都小，就在右子树中寻找LCA，否则当前节点就是LCA。
//主函数
Node *find_LCA(int val1, int val2) {
return find_LCA(_root, val1, val2);
}
//重载的递归函数
Node *find_LCA(Node *root, int val1, int val2) {
//利用后序遍历找到第一个介于val1和val2之间的值
if (root == nullptr) {
return nullptr;
}
if (root->_val < val1 && root->_val < val2) {
return find_LCA(root->_right, val1, val2);
} else if (root->_val > val1 && root->_val > val2) {
return find_LCA(root->_left, val1, val2);
} else {
return root;
}
}
十一、判断一棵树是否为另一棵树的子树
首先在大树中寻找小树的根节点，如果没有找到，说明并非是子树，如果找到了，从该节点开始，分别向左右子树进行遍历。
//主函数
bool is_child_tree(Node *tree) {
return is_child_tree(_root, tree);
}
//重载递归函数
bool is_child_tree(Node *root, Node *tree) {
//当前树和tree都是空返回true
if (root == nullptr && tree == nullptr) {
return true;
}
//只有当前树是空，返回false
if (root == nullptr) {
return false;
}
//只有tree是空，返回true
if (tree == nullptr) {
return true;
}
//在当前树中找到根节点
Node *cur = root;
while (cur != nullptr) {
if (cur->_val < tree->_val) {
cur = cur->_right;
} else if (cur->_val > tree->_val) {
cur = cur->_left;
} else {
break;
}
}
//如果没有在当前树中找到节点，返回false
if (cur == nullptr) {
return false;
}
return is_child_tree(cur->_left, tree->_left) && is_child_tree(cur->_right, tree->_right);
}
十二、根据前序和中序构建一棵二叉树
前序的第一个元素是根节点，在中序中，根节点左边为左子树中所有的节点，右边为右子树中所有的节点，根据此思想，在序列中标记范围进行递归构建，直到范围不合法。
//重载的递归函数
Node *construct_tree(vector<int> &vec1, int begin1, int end1, vector<int> &vec2, int begin2, int end2) {
if (end1 == begin1 && end2 == begin2) {
if (vec1[begin1] == vec2[begin2]) {
return new Node(vec1[begin1]);
}
}
if (end1 < begin1 || end2 < begin2) {
return nullptr;
}
Node *root = new Node(vec1[begin1]);
int mid;
for (mid = begin2; mid <= end2; mid++) {
if (vec2[mid] == vec1[begin1]) {
break;
}
}
root->_left = construct_tree(vec1, begin1 + 1, begin1 + mid - begin2, vec2, begin2, mid - 1);
root->_right = construct_tree(vec1, begin1 + mid - begin2 + 1, end1, vec2, mid + 1, end2);
return root;
}
//主函数
Node *construct_tree(vector<int> &pre_order, vector<int> &in_order) {
return construct_tree(pre_order, 0, pre_order.size() - 1, in_order, 0, in_order.size() - 1);
}
十三、二叉树的构造和析构
二叉树的构造，直接将root初始化为nullptr，
二叉树的析构，使用层次遍历依次的将节点进行回收。
十四、BST的插入，删除，查找操作
插入和查找操作都可以使用递归或者迭代，按照BST的排序性质进行实现，比较简单。
删除操作需要考虑到被删除的元素如果是：
叶子节点，可以直接删除；
如果有一个孩子节点，将其孩子节点赋值为其父节点的孩子；
如果有两个孩子节点，需要使用被删除节点的前驱节点或者后继节点将待删除节点的值覆盖，然后删除前驱或者后继节点。在BST中，一个节点的前驱节点为其左子树中最右的节点，后继节点为其右子树中最左的节点。
十五、AVL树的插入和删除操作
AVL本身也是一个BST，只不过每一个节点都是平衡的，节点平衡即该节点的左右子树高度差不大于1，我们在对AVL进行改变的时候需要随时调整保持平衡的性质。
节点失衡的四种情况（本质是左右子树高度相差大于1）：
左子树比右子树高出1层以上
1.1 左孩子的左子树比右子树高
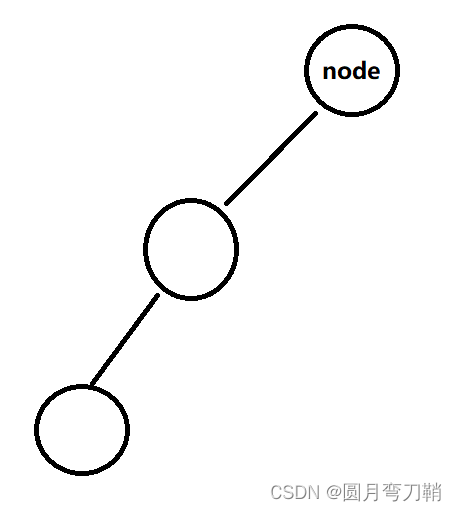
解决办法：右旋转，将node的左孩子调整为根节点，node调整到根节点右侧。
1.2 左孩子的右子树比左子树高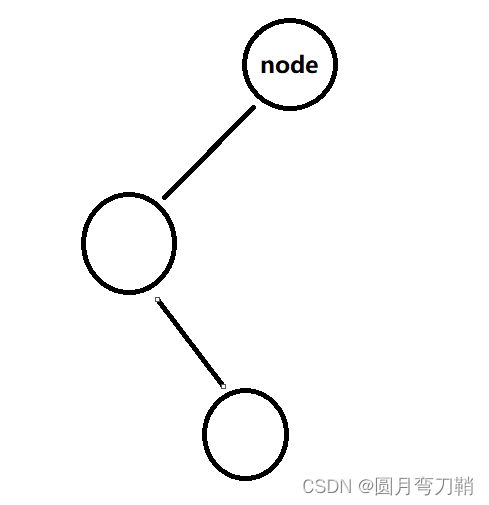
解决办法：先以node的左孩子为根节点进行左旋操作，然后在以node为根节点进行右旋操作。
右子树比左子树高高出1层以上
2.1 右孩子的右子树比左子树高
解决办法：左旋操作，将node的右孩子调整为根节点，将node调整为根节点的左孩子。
2.2 右孩子的左子树比右子树高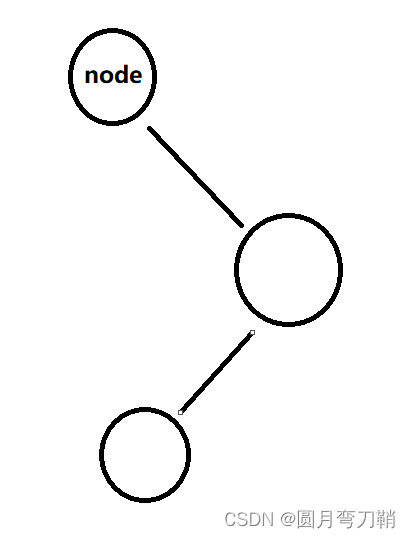
解决办法：先以node的右孩子为根节点进行右旋操作，然后在以node为根节点进行左旋操作。
代码示例：
struct Node {
int height_;
int val_;
Node *left_;
Node *right_;
int height(Node *node) {
//计算节点的高度
if (node == nullptr) {
return 0;
}
return max(height(node->left_), height(node->right_)) + 1;
}
Node(int val = 0) : left_(nullptr), right_(nullptr), val_(val), height_(0) {
}
};
class AVLTree {
public:
AVLTree(Node *root = nullptr) : root_(root) {
}
~AVLTree() {
}
int height(Node *node) {
//计算节点的高度
if (node == nullptr) {
return 0;
}
return max(height(node->left_), height(node->right_)) + 1;
}
Node *leftRotate(Node *node) {
//左旋转操作
Node *child = node->right_;
node->right_ = child->left_;
child->left_ = node;
node->height_ = height(node);
child->height_ = height(node);
return child;
}
Node *rightRotate(Node *node) {
//右旋转操作
Node *child = node->left_;
node->left_ = child->right_;
child->right_ = node;
node->height_ = height(node);
child->height_ = height(node);
return child;
}
Node *rightBalance(Node *node) {
//右平衡操作，先对node的右孩子进行右旋，然后再对node进行左旋
node->right_ = rightRotate(node->right_);
return leftRotate(node);
}
Node *leftBalance(Node *node) {
//左平衡操作，先对node的左孩子进行左旋，然后再对node进行右旋
node->left_ = leftRotate(node->left_);
return rightRotate(node);
}
void insert(int val) {
root_ = insert(root_, val);
}
Node *insert(Node *node, int val) {
if (node == nullptr) {
return new Node(val);
}
if (node->val_ < val) {
//向右子树进行插入，有可能使当前节点失衡
node->right_ = insert(node->right_, val);
if (height(node->right_) - height(node->left_) > 1) {
//向右子树插入使节点node失衡，判断需要左左旋转还是右平衡
if (height(node->right_->right_) >= height(node->right_->left_)) {
node = leftRotate(node);
} else {
node = rightBalance(node);
}
}
} else if (node->val_ > val) {
//向左子树进行插入，有可能使当前节点失衡
node->left_ = insert(node->left_, val);
if (height(node->left_) - height(node->right_) > 1) {
//向左子树插入使节点node失衡，判断需要右旋转还是左平衡
if (height(node->left_->left_) >= height(node->left_->right_)) {
node = rightRotate(node);
} else {
node = leftBalance(node);
}
}
}
//更新节点的高度
node->height_ = height(node);
return node;
}
void remove(int val) {
root_ = remove(root_, val);
}
Node *remove(Node *node, int val) {
if (node == nullptr) {
return nullptr;
}
if (node->val_ < val) {
node->right_ = remove(node->right_, val);
//从右子树删除可能造成左子树太高从而失衡，需要判断进行调整
if (height(node->left_) - height(node->right_) > 1) {
//左子树太高而失衡
if (height(node->left_->left_) >= height(node->left_->right_)) {
node = rightRotate(node);
} else {
node = leftBalance(node);
}
}
} else if (node->val_ > val) {
node->left_ = remove(node->left_, val);
//删除左子树节点可能导致右子树太高，需要判断是否失衡
if (height(node->right_) - height(node->left_) > 1) {
//右子树太高而失衡
if (height(node->right_->right_) >= height(node->right_->left_)) {
node = leftRotate(node);
} else {
node = rightBalance(node);
}
}
} else {
//找到了要移除的节点
if (node->right_ != nullptr && node->left_ != nullptr) {
//要移除的节点有两个孩子，判断左子树和右子树哪个更高，找到前驱或者后继节点进行替换并删除
if (height(node->left_) >= height(node->right_)) {
//左子树比右子树高，找前驱节点进行替换并删除
Node *pre = node->left_;
while (pre->right_ != nullptr) {
pre = pre->right_;
}
node->val_ = pre->val_;
node->left_ = remove(node->left_, pre->val_);
} else {
//右子树比左子树高，找后继节点进行替换并删除
Node *post = node->right_;
while (post->left_ != nullptr) {
post = post->left_;
}
node->val_ = post->val_;
node->right_ = remove(node->right_, post->val_);
}
} else {
//节点最多有一个孩子节点
Node *child = node->left_;
if (node->right_ != nullptr) {
child = node->right_;
}
delete node;
node = nullptr;
return child;
}
}
node->height_ = height(node);
return node;
}
private:
Node *root_;
};
十六、红黑树插入和删除操作
红黑树也是一颗BST
红黑树的5条性质：
- 每个节点都有颜色，不是红色就是黑色；
- nullptr是黑色；
- 根节点是黑色；
- 父节点和子节点不能出现连续两个红色（可以出现连续两个黑色）；
- 从根节点到叶子节点的每一条路径上，黑色节点的数目是相等的。
二叉树的非递归旋转操作
递归旋转操作有返回值，节点与父节点的关系连接是使用递归返回值进行自动操作的，非递归旋转的时候就需要考虑对节点的父节点进行赋值。
如此下图所示对node节点进行左旋操作，需要操作如果所示6个地方的指针。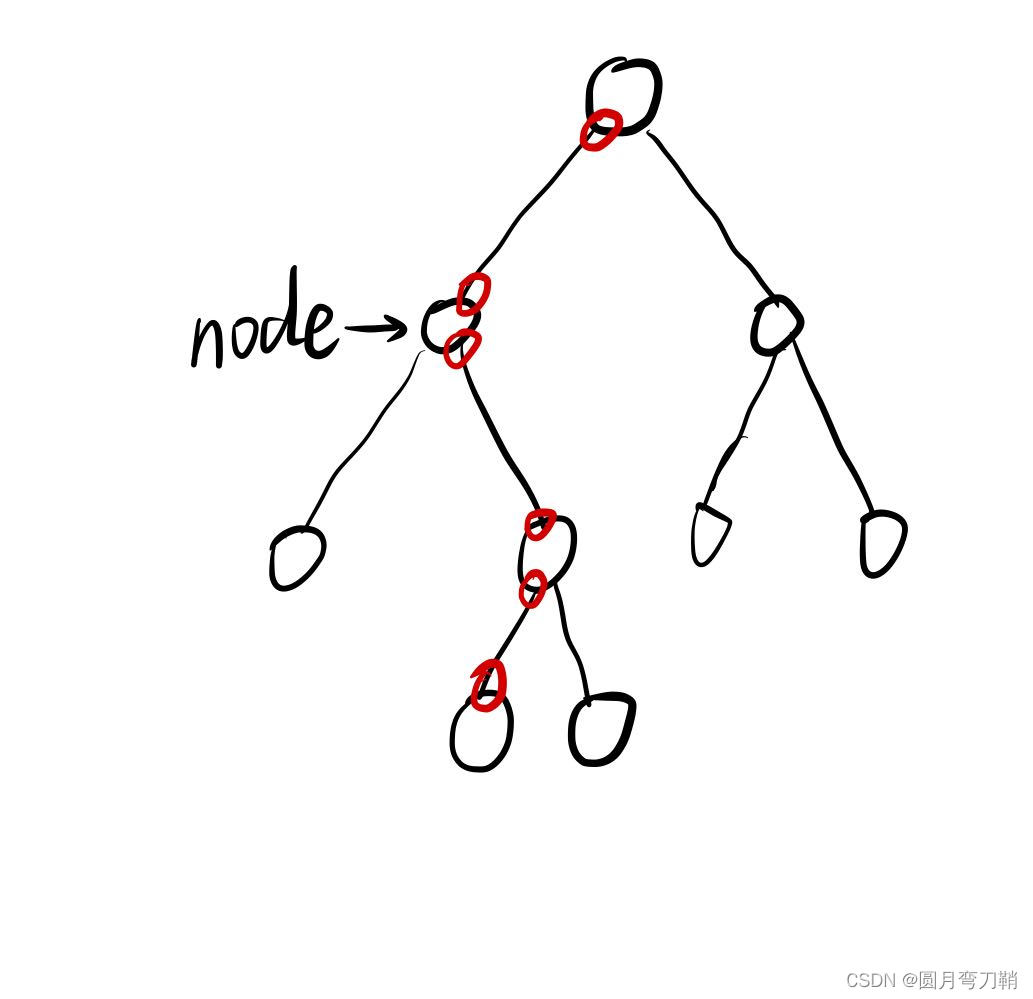
红黑树的插入操作
红黑树的基本插入和BST的插入同理，只不过在插入之后要对树进行调整以保持红黑树的性质。
为了尽量保持红黑树的性质，新插入的节点都是红色的，在红黑树插入的最后，要强制将根节点颜色调整成黑色以保持红黑树的性质。
红黑树的插入调整分为以下3种情况：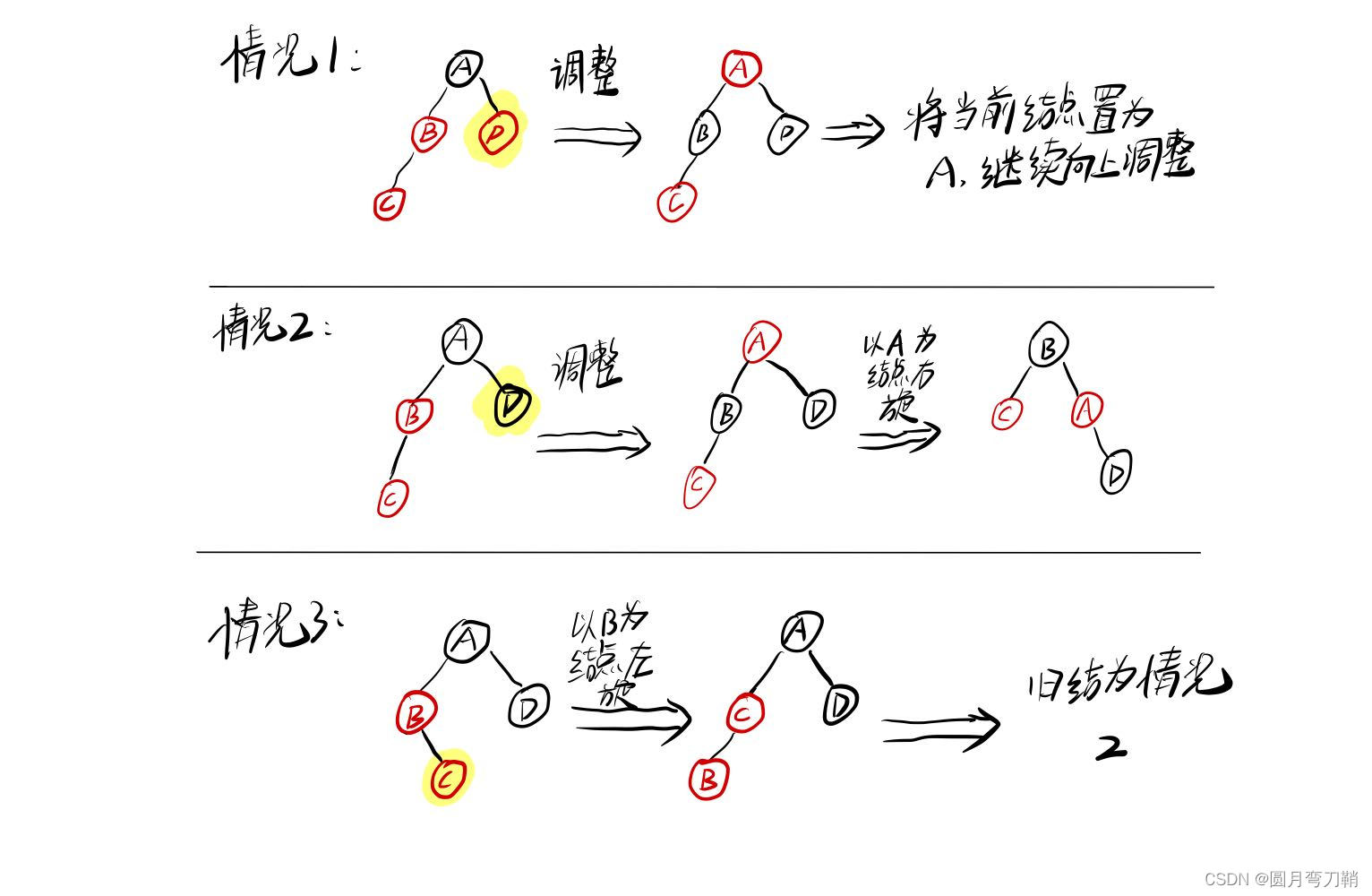
红黑树的节点删除操作
红黑树的删除遵循以下判断步骤
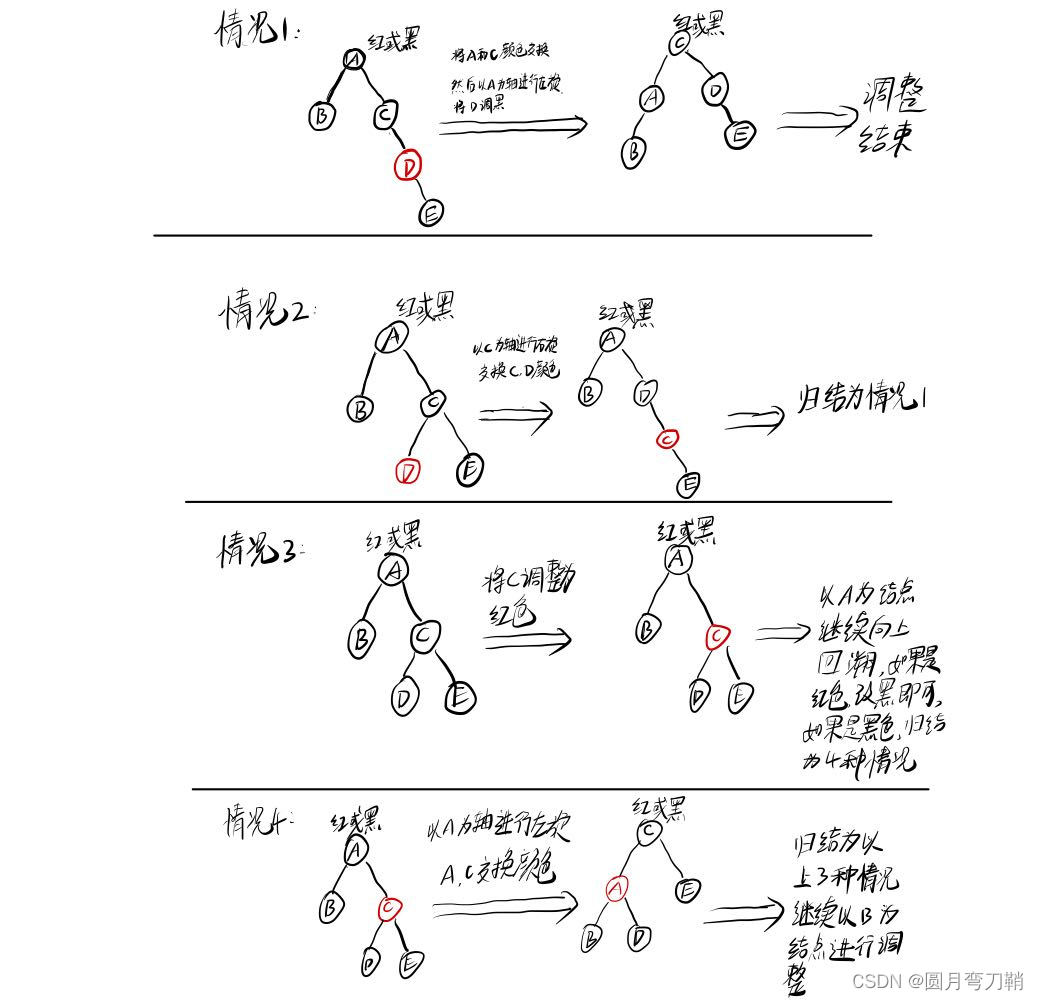
红黑树操作相关代码
#include "iostream"
#include "queue"
using namespace std;
enum Color {
RED,
BLACK
};
struct Node {
int val_;
Node *left_;
Node *right_;
Color color_;
Node *parent_;
explicit Node(int val = 0) : val_(val), left_(nullptr), right_(nullptr), color_(RED), parent_(nullptr) {
}
};
class RBTree {
public:
explicit RBTree(Node *root = nullptr) : root_(root) {
}
~ RBTree() {
if (root_ == nullptr) {
return;
}
queue<Node *> q;
q.push(root_);
while (!q.empty()) {
Node *cur = q.front();
if (cur->left_ != nullptr) {
q.push(cur->left_);
}
if (cur->right_ != nullptr) {
q.push(cur->right_);
}
q.pop();
delete cur;
cur = nullptr;
}
};
Color getColor(Node *node) {
if (node == nullptr) {
return BLACK;
} else {
return node->color_;
}
}
void leftRotate(Node *node) {
Node *child = node->right_;
child->parent_ = node->parent_;
if (node->parent_ == nullptr) {
root_ = child;
} else {
if (node->parent_->left_ == node->parent_) {
node->parent_->left_ = child;
} else {
node->parent_->right_ = child;
}
}
node->right_ = child->left_;
if (child->left_ != nullptr) {
child->left_->parent_ = node;
}
child->left_ = node;
node->parent_ = child;
}
void rightRotate(Node *node) {
Node *child = node->left_;
child->parent_ = node->parent_;
if (node->parent_ == nullptr) {
root_ = child;
} else {
if (node->parent_->left_ == node) {
node->parent_->left_ = child;
} else {
node->parent_->right_ = child;
}
}
node->left_ = child->right_;
if (child->right_ != nullptr) {
child->right_->parent_ = node;
}
child->right_ = node;
node->parent_ = child;
}
void insert(int val) {
if (root_ == nullptr) {
root_ = new Node(val);
root_->color_ = BLACK;
return;
}
Node *parent = nullptr;
Node *cur = root_;
while (cur != nullptr) {
if (cur->val_ < val) {
parent = cur;
cur = cur->right_;
} else if (cur->val_ > val) {
parent = cur;
cur = cur->left_;
} else {
//发现重复的节点，停止插入
return;
}
}
//找到了要插入的位置
cur = new Node(val);
cur->parent_ = parent;
if (val > parent->val_) {
parent->right_ = cur;
} else {
parent->left_ = cur;
}
//开始判断是否需要进行红黑树调整
if (getColor(parent) == BLACK) {
//如果父节点是黑色，则红黑树性质未被破坏，插入完成
return;
}
adjustAfterInsert(cur);
}
void adjustAfterInsert(Node *node) {
while (getColor(node->parent_) == RED) {
if (node->parent_->parent_->left_ == node->parent_) {
//插入的节点在祖父节点的左子树
Node *uncle = node->parent_->parent_->right_;
if (getColor(uncle) == RED) {
//情况1
uncle->color_ = BLACK;
node->parent_->color_ = BLACK;
node->parent_->parent_->color_ = RED;
node = node->parent_->parent_;
} else {
//情况2和情况3
//情况3可以归结为情况2，所以先处理情况3
if (node->parent_->right_ == node) {
//情况3
node = node->parent_;
leftRotate(node);
}
//情况2
node->parent_->color_ = BLACK;
node->parent_->parent_->color_ = RED;
rightRotate(node->parent_->parent_);
break;
}
} else {
//插入的节点在祖父节点右子树
Node *uncle = node->parent_->parent_->left_;
if (getColor(uncle) == RED) {
//情况1
uncle->color_ = BLACK;
node->parent_->color_ = BLACK;
node->parent_->parent_->color_ = RED;
node = node->parent_->parent_;
} else {
//情况2和情况3
//情况3可以归结为情况2，所以先处理情况3
if (node->parent_->left_ == node) {
//情况3
node = node->parent_;
rightRotate(node);
}
//情况2
node->parent_->color_ = BLACK;
node->parent_->parent_->color_ = RED;
leftRotate(node->parent_->parent_);
break;
}
}
}
//最后都要将根节点颜色置为黑色
root_->color_ = BLACK;
}
void remove(int val) {
if (root_ == nullptr) {
return;
}
//寻找需要删除的节点
Node *cur = root_;
while (cur != nullptr) {
if (val < cur->val_) {
cur = cur->left_;
} else if (val > cur->val_) {
cur = cur->right_;
} else {
break;
}
}
if (cur == nullptr) {
//没有找到要删除的节点
return;
}
//找到了要删除的节点
if (cur->left_ != nullptr && cur->right_ != nullptr) {
//如果要删除的节点有两个孩子
Node *pre = cur->left_;
while (pre->right_ != nullptr) {
pre = pre->right_;
}
cur->val_ = pre->val_;
cur = pre;
}
//寻找被删除节点的子节点
Node *child = cur->left_;
if (cur->right_ != nullptr) {
child = cur->right_;
}
if (child != nullptr) {
child->parent_ = cur->parent_;
if (cur->parent_ == nullptr) {
root_ = child;
} else {
if (cur->val_ < cur->parent_->val_) {
cur->parent_->left_ = child;
} else {
cur->parent_->right_ = child;
}
}
if (getColor(cur) == BLACK) {
if (getColor(child) == RED) {
child->color_ = BLACK;
} else {
adjustAfterRemove(child);
}
}
delete cur;
cur = nullptr;
} else {
if (cur->parent_ == nullptr) {
root_ = nullptr;
} else {
if (getColor(cur) == BLACK) {
adjustAfterRemove(cur);
}
if (cur->val_ < cur->parent_->val_) {
cur->parent_->left_ = nullptr;
} else {
cur->parent_->right_ = nullptr;
}
}
delete cur;
cur = nullptr;
}
}
void adjustAfterRemove(Node *node) {
while (getColor(node) == BLACK) {
if (node->parent_ == nullptr) {
//node是根节点
break;
}
if (node == node->parent_->left_) {
//补位节点在父节点的左侧
Node *sibling = node->parent_->right_;
if (getColor(sibling) == RED) {
//情况4
sibling->color_ = BLACK;
node->parent_->color_ = RED;
leftRotate(node->parent_);
sibling = node->parent_->right_;
}
if (getColor(sibling->left_) == BLACK && getColor(sibling->right_) == BLACK) {
//情况3
sibling->color_ = RED;
node = node->parent_;
continue;
}
if (getColor(sibling->right_) == BLACK) {
//情况2
sibling->color_ = RED;
sibling->left_->color_ = BLACK;
rightRotate(sibling);
sibling = node->parent_->right_;
}
//情况1
sibling->color_ = node->parent_->color_;
node->parent_->color_ = BLACK;
leftRotate(node->parent_);
sibling->right_->color_ = BLACK;
break;
} else {
// 补位节点在父节点的右侧
Node *sibling = node->parent_->left_;
if (getColor(sibling) == RED) {
//情况4
sibling->color_ = BLACK;
node->parent_->color_ = RED;
rightRotate(node->parent_);
sibling = node->parent_->left_;
}
if (getColor(sibling->left_) == BLACK && getColor(sibling->right_) == BLACK) {
//情况3
sibling->color_ = RED;
node = node->parent_;
continue;
}
if (getColor(sibling->left_) == BLACK) {
//情况2
sibling->color_ = RED;
sibling->right_->color_ = BLACK;
leftRotate(sibling);
sibling = node->parent_->left_;
}
//情况1
sibling->color_ = node->parent_->color_;
node->parent_->color_ = BLACK;
rightRotate(node->parent_);
sibling->left_->color_ = BLACK;
break;
}
}
node->color_ = BLACK;
}
private:
Node *root_;
};
int main() {
int a[] = {
1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
RBTree tree;
for (auto i: a) {
tree.insert(i);
}
tree.remove(9);
tree.remove(10);
tree.remove(5);
tree.remove(3);
system("pause");
return 0;
}
边栏推荐
猜你喜欢
随机推荐
【命令执行与中间件漏洞】
动态调整web系统主题? 看这一篇就够了
极光推送 能否缓存 消息
【反弹shell与提权】
The ` monorepo ` ` hoist ` mechanism lead to the change of the loading configuration file path
当奈飞的NFT忘记了web2的业务安全
Apache2-XXE漏洞渗透
东南亚跨境电商
IO 复用
MySQL 排序
令人愉快的 Nuxt3 教程 (一): 应用的创建与配置
block底层探索
用iPhone前摄3D人像建模，Meta：我看行
Leetcode刷题——128. 最长连续序列
Greetings（状压DP，枚举子集转移）
The result of request.getParameter is on
Invalid signature file digest for Manifest main attributes解决方法
速来围观，17个运维实用技巧
EIP-5058 能否防止NFT项目方提桶跑路？
Mysql 预准备语句详解（prepare、execute、deallocate）