当前位置:网站首页>Matlab学习12-图像处理之图像增强
Matlab学习12-图像处理之图像增强
2022-08-03 11:30:00 【CHengYuP】
前言
图像增强基本思路是:
允许一定频率通过(保留某些频率分量),限制或消减另外一些频率(消除某些频率分量)。
转移函数的优劣是滤波器优劣的关键。
频域增强方法根据滤波特点,特别是消除或保留的频率分量可以分为:
- 低通滤波
基本原理:
保留图像中的低频分量而除去高频分量。
作用:
除去或消弱噪声影响并模糊边缘轮廓,属于图像平滑处理技术。因为:图像中的边缘和噪声对应图像傅里叶频谱中的高频部分。
包括:
·理想低通滤波器(ILPF)
·巴特沃斯低通滤波器(BLPF)
·指数低通滤波器(ELPF)
·梯形低通滤波器(TLPF)
·高斯低通滤波器(GLPF)
- 高通滤波
基本原理:
保留图像中的高频分量而除去低频分量。
作用:
突出物体边缘轮廓,属于图像锐化处理技术。
因为:图像中的边缘对应图像傅里叶频谱中的高频部分。
效果:
锐化物体边缘,但光滑区域灰度减弱、变暗甚至接近黑色。
因为:图像中大部分能量集中在低频分量里,高通滤波将会滤除大部分低频分量。
包括:
·理想高通滤波器(IHPF)
·巴特沃斯高通滤波器(BHPF)
·指数高通滤波器(EHPF)
·梯形高通滤波器(THPF)
·高斯高通滤波器(GHPF)
·高频增强滤波器
·高频提升滤波器
- 带通&带阻滤波
- 同态滤波
一、理想低通滤波
效果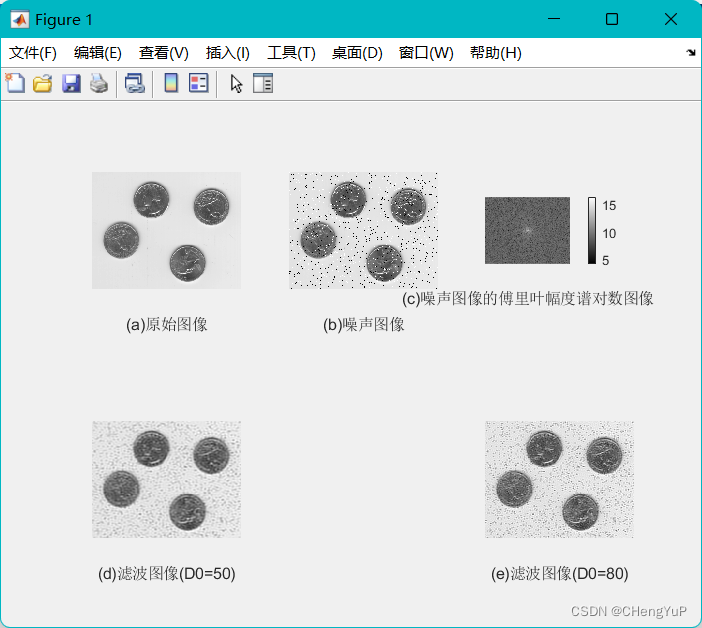
代码
%理想低通滤波
f1xy=imread("img/eight.tif");
subplot(2,3,1),imshow(f1xy),xlabel("(a)原始图像");
f2xy=imnoise(f1xy,'salt & pepper',0.05);
subplot(2,3,2),imshow(f2xy),xlabel("(b)噪声图像");
fxy=double(f2xy);
Fuv=fft2(fxy);
FftShift=fftshift(Fuv);
AbsFftShift=abs(FftShift);
LogAbsFftShift=log(AbsFftShift);
subplot(2,3,3),imshow(LogAbsFftShift,[]),xlabel("(c)噪声图像的傅里叶幅度谱对数图像"),colormap(gray),colorbar;
%图的尺寸
[N1,N2]=size(FftShift);
% 截至频率D0=50时的滤波效果
D0=50;
%中心点
n1=fix(N1/2);
n2=fix(N2/2);
for i=1:N1
for j=1:N2
d=sqrt((i-n1)^2+(j-n2)^2);
if(d<D0)
G(i,j)=FftShift(i,j);
else
G(i,j)=0;
end
end
end
% 反变换
G=ifftshift(G);
g=ifft2(G);
g=uint8(real(g));
subplot(2,3,4),imshow(g),xlabel("(d)滤波图像(D0=50)");
D0=80;
for i=1:N1
for j=1:N2
d=sqrt((i-n1)^2+(j-n2)^2);
if(d<D0)
G(i,j)=FftShift(i,j);
else
G(i,j)=0;
end
end
end
% 反变换
G=ifftshift(G);
g=ifft2(G);
g=uint8(real(g));
subplot(2,3,6),imshow(g),xlabel("(e)滤波图像(D0=80)");
二、巴特沃斯低通滤波
效果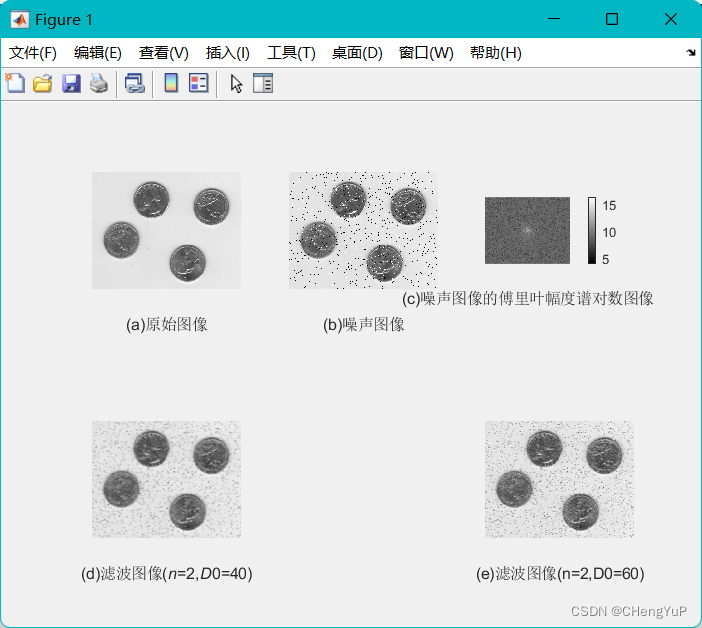
代码
% 巴特沃斯低通滤波
f1xy=imread("img/eight.tif");
subplot(2,3,1),imshow(f1xy),xlabel("(a)原始图像");
f2xy=imnoise(f1xy,'salt & pepper',0.05);
subplot(2,3,2),imshow(f2xy),xlabel("(b)噪声图像");
% 傅里叶变换
fxy=double(f2xy);
Fuv=fft2(fxy);
FftShift=fftshift(Fuv);
AbsFftShift=abs(FftShift);
LogAbsFftShift=log(AbsFftShift);
subplot(2,3,3),imshow(LogAbsFftShift,[]),xlabel("(c)噪声图像的傅里叶幅度谱对数图像"),colormap(gray),colorbar;
[N1,N2]=size(FftShift);
% 阶数n=2,截至频率D0=40时的滤波效果
n=2;
D0=40;
%中心点
n1=fix(N1/2);
n2=fix(N2/2);
for i=1:N1
for j=1:N2
d=sqrt((i-n1)^2+(j-n2)^2);
H=1/(1+(sqrt(2)-1)*(d/D0)^(2*n));
G(i,j)=H*FftShift(i,j);
end
end
% 反变换
G=ifftshift(G);
g=ifft2(G);
g=uint8(real(g));
subplot(2,3,4),imshow(g),xlabel("(d)滤波图像({\itn}=2,{\itD}0=40)");
% 阶数n=2,截至频率D0=60时的滤波效果
n=2;
D0=60;
%中心点
n1=fix(N1/2);
n2=fix(N2/2);
for i=1:N1
for j=1:N2
d=sqrt((i-n1)^2+(j-n2)^2);
H=1/(1+(sqrt(2)-1)*(d/D0)^(2*n));
G(i,j)=H*FftShift(i,j);
end
end
% 反变换
G=ifftshift(G);
g=ifft2(G);
g=uint8(real(g));
subplot(2,3,6),imshow(g),xlabel("(e)滤波图像(n=2,D0=60)");
三、高斯高通滤波
效果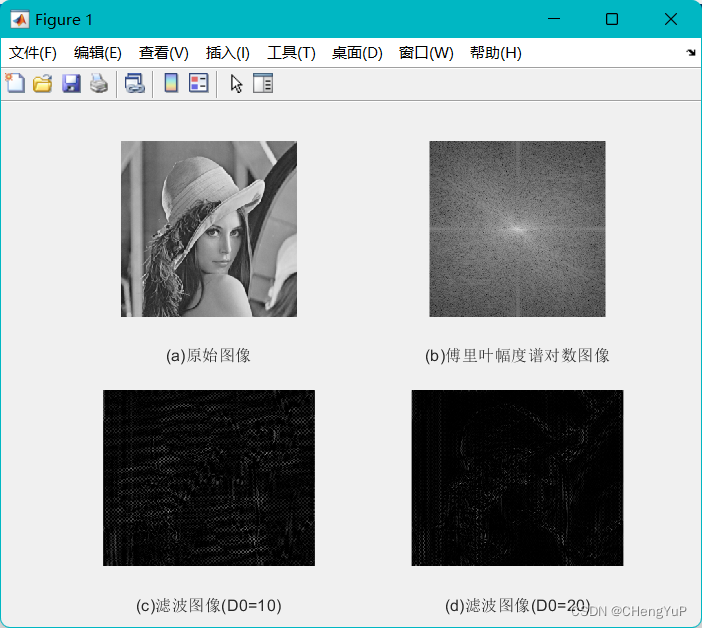
代码
% 高斯高通滤波
fxy=imread("img/lena.bmp");
subplot(2,2,1),imshow(fxy),xlabel("(a)原始图像");
% 傅里叶幅度谱的对数图像显示
fxy=double(fxy);
Fuv=fft2(fxy);%二维傅里叶变换
ShiftFuv=fftshift(Fuv);
AbsShiftFuv=abs(ShiftFuv);%傅里叶幅度谱
LogAbsShiftFuv=log(AbsShiftFuv);%傅里叶幅度谱可视化
subplot(2,2,2),imshow(LogAbsShiftFuv,[]),xlabel("(b)傅里叶幅度谱对数图像");
% 截至频率D0=10时的滤波效果
[N1,N2]=size(ShiftFuv);
D0=10;
%中心点
n1=fix(N1/2);
n2=fix(N2/2);
for i=1:N1
for j=1:N2
d=sqrt((i-n1)^2+(j-n2)^2);
Huv=1-exp(-d^2/(2*D0^2));% 高斯高通公式
G(i,j)=Huv*ShiftFuv(i,j);
end
end
% 反变换
G=ifftshift(G);
g=ifft2(G);
g=uint8(real(g));
subplot(2,2,3),imshow(g),xlabel("(c)滤波图像(D0=10)");
% 截至频率D0=20时的滤波效果
[N1,N2]=size(ShiftFuv);
D0=20;
%中心点
n1=fix(N1/2);
n2=fix(N2/2);
for i=1:N1
for j=1:N2
d=sqrt((i-n1)^2+(j-n2)^2);
Huv=1-exp(-d^2/(2*D0^2));
G(i,j)=Huv*ShiftFuv(i,j);
end
end
% 反变换
G=ifftshift(G);
g=ifft2(G);
g=uint8(real(g));
subplot(2,2,4),imshow(g),xlabel("(d)滤波图像(D0=20)");
总结
频域增强与空域增强的关系
空域滤波增强分为平滑滤波和锐化滤波。
·从空域的角度看,平滑滤波能够减少局部灰度起伏和噪声干扰;
·从频域的角度看,灰度起伏和噪声干扰具有较高的频率,滤除它可以采用具有低通能力的频域滤波器。
空域滤波增强的基本原理是利用图像与模板的卷积来进行。
·根据卷积定理,空域中图像与模板的卷积等于图像的傅里叶变换和模板的傅里叶变换在频域的乘积。
·根据图像频域增强的基本原理,频域图像增强是频域原始图像与频域传递函数的乘积,即图像的傅里叶变换与频域传递函数的乘积。
点击获取源码
边栏推荐
- ThreadLocal源码解析及使用场景
- 当前页面的脚本发生错误如何解决_电脑出现当前页面脚本错误怎么办
- CDH6.3.2开启kerberos认证
- Fastjson反序列化
- Skills required to be a good architect: How to draw a system architecture that everyone will love?What's the secret?Come and open this article to see it!...
- "Global Digital Economy Conference" landed in N World, Rongyun provides communication cloud service support
- 【TypeScript】为什么要选择 TypeScript?
- Activiti产生的背景和作用
- complete knapsack problem
- This article takes you to understand the principle of CDN technology
猜你喜欢
Why is the new earth blurred, in-depth analysis of white balls, viewing pictures, and downloading problems
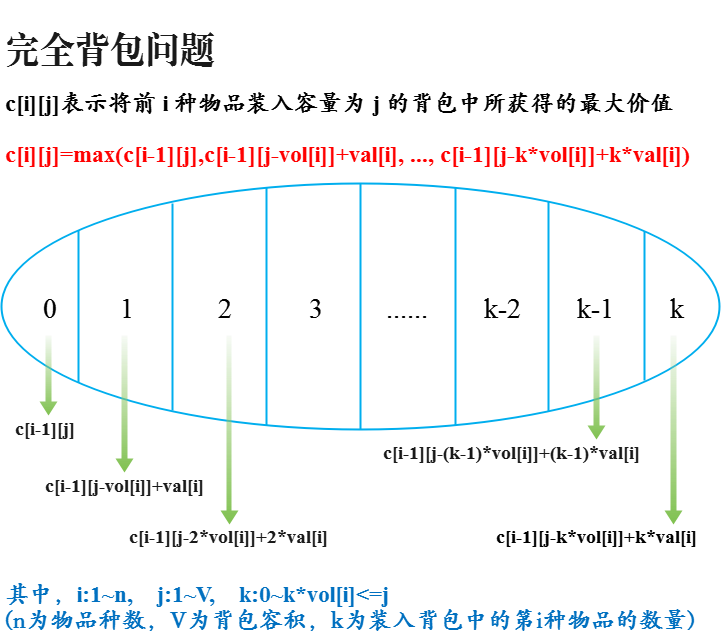
完全背包问题
![LeetCode 899 Ordered queue [lexicographical order] HERODING's LeetCode road](/img/95/1b63cfb25b9e0802666114f089fcb8.png)
LeetCode 899 Ordered queue [lexicographical order] HERODING's LeetCode road
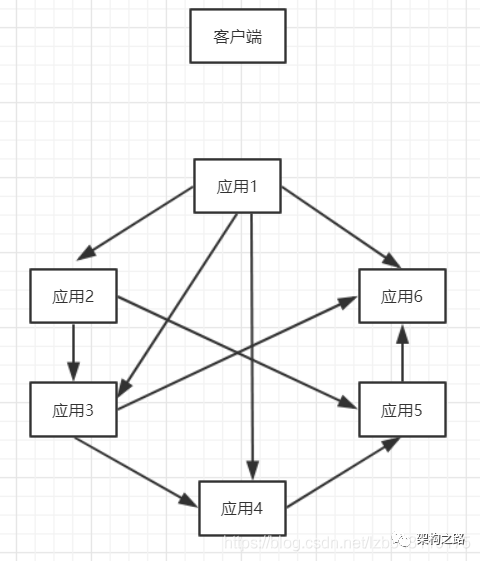
面试官:SOA 和微服务的区别?这回终于搞清楚了!
请问应该用什么关键字将内容主题设置为 dark 呢
基于SSM和Web实现的农作物生长监控系统

技术总监需要会些什么?也太难了!

优维低代码:Provider 构件
一个扛住 100 亿次请求的红包系统,写得太好了!!
![[Bubble sort and odd-even sorting]](/img/89/d63afe1900a05b2a5615fcc3c09ccb.png)
[Bubble sort and odd-even sorting]
随机推荐
【二分查找详解外加递归写法】附有全部代码
Activiti产生的背景和作用
html网页如何获取后台数据库的数据(html + ajax + php + mysql)
CADEditorX ActiveX 14.1.X
笔试题:金额拆分
代码分析Objective-C中的深拷贝与浅拷贝
【一起学Rust 基础篇】Rust基础——变量和数据类型
Realize 2d characters move left and right while jumping
XDR平台架构与关键技术解析
实现2d人物在跳跃的同时左右移动
【文件IO的简单实现】
嵌入式软件组件经典架构与存储器分类
使用.NET简单实现一个Redis的高性能克隆版(一)
RTP协议分析
Programmers architecture practice way: software architecture basic concepts and thinking
实至名归!九章云极DataCanvas公司荣获智能制造领域多项殊荣
数据库一席谈:打造开源的数据生态,支撑产业数字化浪潮
机器比人更需要通证
完全背包问题的思路解析
MapReduce中ETL数据清洗案例