当前位置:网站首页>[错题]电路维修
[错题]电路维修
2022-08-03 10:59:00 【wingaso】
WA代码
#include<bits/stdc++.h>
#define xx first
#define yy second
using namespace std;
typedef pair<int,int> pii;
const int N = 510;
string G[N];
int r,c;
int D[N][N];
const int d1[] = {
-1,-1,1, 1}; // 点
const int d2[] = {
-1, 1,1,-1};
const int k1[] = {
-1,-1,0, 0}; // 边
const int k2[] = {
-1, 0,0,-1};
const char kk[] = "\\/\\/";
int bfs(){
deque<pii> q;
memset(D,-1,sizeof D);
q.push_back({
0,0});
D[0][0] = 0;
while(!q.empty()){
int x = q.front().xx,y = q.front().yy;
q.pop_front();
if(x == r and y == c) break;
for(int i = 0;i < 4;i++){
int dx = x + d1[i],dy = y + d2[i];
int kx = x + k1[i],ky = y + k2[i];
if(dx < 0 or dy < 0 or dx > r or dy > c) continue;
if(~D[dx][dy]) continue;
if(G[kx][ky] == kk[i]){
D[dx][dy] = D[x][y];
q.push_front({
dx,dy});
}
else{
D[dx][dy] = D[x][y] + 1;
q.push_back({
dx,dy});
}
}
}
return D[r][c];
}
int main(){
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(false);
int t; cin >> t;
while(t--){
cin >> r >> c;
for(int i = 0;i < r;i++) cin >> G[i];
cout << bfs() << endl;
}
return 0;
}
AC代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<string>
#include<deque>
#define xx first
#define yy second
using namespace std;
typedef pair<int,int> pii;
const int N = 510;
string G[N];
int r,c;
int D[N][N];
const int d1[] = {
-1,-1,1, 1}; // 点
const int d2[] = {
-1, 1,1,-1};
const int k1[] = {
-1,-1,0, 0}; // 边
const int k2[] = {
-1, 0,0,-1};
const char kk[] = "\\/\\/";
bool st[N][N];
int bfs(){
if((r + c) % 2) return -1;
deque<pii> q;
memset(D,0x3f,sizeof D);
memset(st,false,sizeof st);
q.push_back({
0,0});
D[0][0] = 0;
st[0][0] = true;
while(!q.empty()){
int x = q.front().xx,y = q.front().yy;
q.pop_front();
st[x][y] = true;
if(x == r and y == c) break;
for(int i = 0;i < 4;i++){
int dx = x + d1[i],dy = y + d2[i];
int kx = x + k1[i],ky = y + k2[i];
if(dx < 0 or dy < 0 or dx > r or dy > c) continue;
if(st[dx][dy]) continue;
if(G[kx][ky] == kk[i] and D[dx][dy] > D[x][y]){
D[dx][dy] = D[x][y];
q.push_front({
dx,dy});
}
else if(G[kx][ky] != kk[i] and D[dx][dy] > D[x][y] + 1){
D[dx][dy] = D[x][y] + 1;
q.push_back({
dx,dy});
}
}
}
return D[r][c];
}
int main(){
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(false);
int t; cin >> t;
while(t--){
cin >> r >> c;
for(int i = 0;i < r;i++) cin >> G[i];
int res = bfs();
if(~res) cout << res << endl;
else cout << "NO SOLUTION" << endl;
}
return 0;
}
错误原因
错误原因是,误认为一个点第一次更新时的距离一定为最短距离。
这是一个假命题。
因为在每一次从队列中取出一个点 ( x , y ) (x,y) (x,y)时,会更新其相邻的四个点的"距离"。
当 D [ d x ] [ d y ] = D [ x ] [ y ] + 1 D[dx][dy] =D[x][y] + 1 D[dx][dy]=D[x][y]+1时,仍然不能排除能够从另外一个距离为 D [ t x ] [ t y ] = D [ x ] [ y ] D[tx][ty] = D[x][y] D[tx][ty]=D[x][y]的点 ( t x , t y ) (tx,ty) (tx,ty),以 0 0 0的代价从 ( t x , t y ) (tx,ty) (tx,ty)走到 ( d x , d y ) (dx,dy) (dx,dy)。
双端队列广搜,实际可以理解为dijkstra的简化版本。
我们每一次更新距离,即是一次松弛操作。
所以,我们可以仿照着,将初始距离设置为(理论上的)无穷大,然后在更新中使得最终取得的距离为最小距离。
因此,这里不能使用D数组作为是否需要更新该节点距离的判断依据,我们需要增加一个新的状态数组 s t st st。
边栏推荐
- mysql数据库定时备份占用大量线程,导致全局锁表,有啥好的解决方法么
- 【冒泡排序以及奇数偶数排列】
- [LeetCode—Question 2 Sum of Two Numbers Detailed Code Explanation ] The source code is attached, which can be copied directly
- 完全背包问题
- 请问应该用什么关键字将内容主题设置为 dark 呢
- 成为优秀架构师必备技能:怎样才能画出让所有人赞不绝口的系统架构图?秘诀是什么?快来打开这篇文章看看吧!...
- build --repot
- 浪潮—英伟达打造元宇宙新方案,虚拟人的故事将再破你的认知
- 微信多开批处理(自动获取安装路径)
- ARIMA实现(亲测可用)
猜你喜欢
深度学习100例——卷积神经网络(CNN)实现服装图像分类

For invoice processing DocuWare, cast off the yoke of the paper and data input, automatic processing all the invoice received
2022年五面蚂蚁、三面拼多多、字节跳动最终拿offer入职拼多多
MySQL数据库基本使用
MapReduce中ETL数据清洗案例
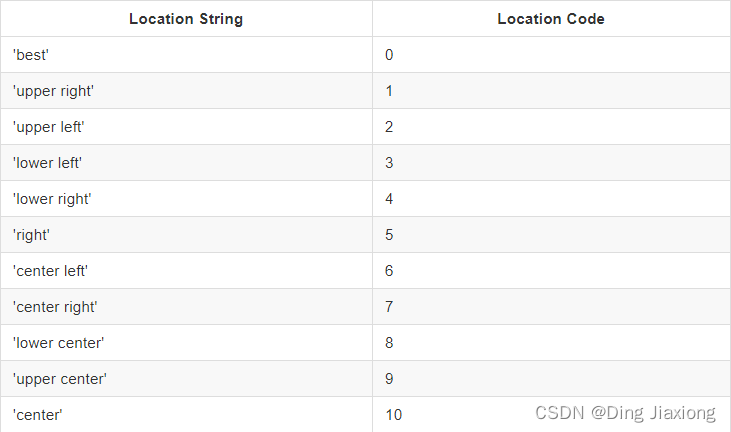
Matplotlib
![[Star Project] Little Hat Plane Battle (9)](/img/e3/c7d2728080bcdccc181a7e5c50ee6f.png)
[Star Project] Little Hat Plane Battle (9)

ETL data cleaning case in MapReduce

创建C UDR时,指定的HANDLESNULLS的作用是什么?

What is the relationship between The Matrix and 6G?
随机推荐
机器比人更需要通证
鸿蒙第三次
Advanced use of MySQL database
ETL data cleaning case in MapReduce
开源一夏 | 教你快速实现“基于Docker快速构建基于Prometheus的MySQL监控系统”
C#+WPF 单元测试项目类高级程序员必知必会
CADEditorX ActiveX 14.1.X
成为优秀架构师必备技能:怎样才能画出让所有人赞不绝口的系统架构图?秘诀是什么?快来打开这篇文章看看吧!...
【Star项目】小帽飞机大战(九)
从餐桌到太空,孙宇晨的“星辰大海”
Machine Learning Overview
面试一面
Web Server 设置缓存响应字段的一些推荐方案
Classical Architecture and Memory Classification of Embedded Software Components
使用.NET简单实现一个Redis的高性能克隆版(一)
MATLAB Programming and Applications 2.6 Strings
玉溪卷烟厂通过正确选择时序数据库 轻松应对超万亿行数据
Activiti产生的背景和作用
巴比特 | 元宇宙每日必读:玩家离场,平台关停,数字藏品市场正逐渐降温,行业的未来究竟在哪里?...
[Explanation of JDBC and inner classes]