当前位置:网站首页>[combinatorics] generating function (positive integer splitting | unordered | ordered | allowed repetition | not allowed repetition | unordered not repeated splitting | unordered repeated splitting)
[combinatorics] generating function (positive integer splitting | unordered | ordered | allowed repetition | not allowed repetition | unordered not repeated splitting | unordered repeated splitting)
2022-07-03 18:05:00 【Programmer community】
List of articles
- One 、 Positive integer split
- Two 、 Unordered split
- 1、 Unordered split No repetition
- 2、 Unordered split Allow repetition
Reference blog :
- 【 Combinatorial mathematics 】 Generating function Brief introduction ( Generating function definition | Newton's binomial coefficient | Common generating functions | Related to constants | Related to binomial coefficient | Related to polynomial coefficients )
- 【 Combinatorial mathematics 】 Generating function ( Linear properties | Product properties )
- 【 Combinatorial mathematics 】 Generating function ( Shift property )
- 【 Combinatorial mathematics 】 Generating function ( The nature of summation )
- 【 Combinatorial mathematics 】 Generating function ( Commutative properties | Derivative property | Integral properties )
- 【 Combinatorial mathematics 】 Generating function ( Summary of nature | Important generating functions ) *
- 【 Combinatorial mathematics 】 Generating function ( Generate function examples | Given the general term formula, find the generating function | Given the generating function, find the general term formula )
- 【 Combinatorial mathematics 】 Generating function ( Generate function application scenarios | Solving recursive equations using generating functions )
- 【 Combinatorial mathematics 】 Generating function ( Use the generating function to solve multiple sets r Combinatorial number )
- 【 Combinatorial mathematics 】 Generating function ( Use generating function to solve the number of solutions of indefinite equation )
- 【 Combinatorial mathematics 】 Generating function ( Examples of using generating functions to solve the number of solutions of indefinite equations )
- 【 Combinatorial mathematics 】 Generating function ( Examples of using generating functions to solve the number of solutions of indefinite equations 2 | Extended to integer solutions )
One 、 Positive integer split
Positive integer split Contents involved :
- Split definition and classification
- Unordered split
- Orderly splitting
A positive integer can Split into several positive integers And , Each different split method , Can As a plan ;
Sort according to the splitting order :
4
4
4 Split into
1
1
1 and
3
3
3 ,
4
4
4 Split into
3
3
3 and
1
1
1 ;
- Orderly splitting : Above
2
2
2 individual Positive integer split , yes Two different splitting methods ;
- Unordered split : Above
2
2
2 individual Positive integer split , yes The same split method ;
Classify according to whether it is repeated :
- Allow repetition : When splitting , It is allowed to split into several repeated positive integers , Such as
3
3
3 Split into
3
3
3 individual
1
1
1 ;
- No repetition : When splitting , Split positive integer No repetition , Such as
3
3
3 Split into
3
3
3 individual
1
1
1 It's wrong. , Can only be split into
1
,
2
1,2
1,2 ;
Positive integer splitting can be done by nature , It is divided into
4
4
4 class ;
- Orderly repetition
- Order does not repeat
- Disorderly repetition
- Disorder does not repeat
Two 、 Unordered split
Unordered split basic model :
take Positive integer
N
N
N Unordered split into positive integers ,
a
1
,
a
2
,
⋯
,
a
n
a_1, a_2, \cdots , a_n
a1,a2,⋯,an It is a split
n
n
n Number ,
The split is unordered , Split above
n
n
n The number of numbers may be different ,
hypothesis
a
1
a_1
a1 Yes
x
1
x_1
x1 individual ,
a
2
a_2
a2 Yes
x
2
x_2
x2 individual ,
⋯
\cdots
⋯ ,
a
n
a_n
an Yes
x
n
x_n
xn individual , Then there is the following equation :
a
1
x
1
+
a
2
x
2
+
⋯
+
a
n
x
n
=
N
a_1x_1 + a_2x_2 + \cdots + a_nx_n = N
a1x1+a2x2+⋯+anxn=N
This form can be used Number of nonnegative integer solutions of indefinite equation Generation function calculation of , yes With coefficients , With restrictions , Reference resources : Combinatorial mathematics 】 Generating function ( Use generating function to solve the number of solutions of indefinite equation )
In the case of unordered splitting , A positive integer after splitting , Allow repetition and No repetition , It is two kinds of combinatorial problems ;
If No repetition , So these
x
i
x_i
xi The value of , Can only Value
0
,
1
0, 1
0,1 ; amount to With restrictions , With coefficients Of Nonnegative integer solutions of indefinite equations The situation of ;
If Allow repetition , So these
x
i
x_i
xi The value of , Namely Natural number ; amount to With coefficients Of Nonnegative integer solutions of indefinite equations The situation of ;
1、 Unordered split No repetition
Discuss Unordered split , Repetition is not allowed , This way Equivalent to With restrictions , With coefficients Of Nonnegative integer solutions of indefinite equations The situation of ;
a
1
a_1
a1 Item corresponds to the generating function item ,
x
1
x_1
x1 Value
0
,
1
0,1
0,1 , Then the corresponding generating function item is
(
y
a
1
)
0
+
(
y
a
1
)
1
=
1
+
y
a
1
(y^{a_1})^{0} + (y^{a_1})^{1}= 1+ y^{a_1}
(ya1)0+(ya1)1=1+ya1
a
2
a_2
a2 Item corresponds to the generating function item ,
x
2
x_2
x2 Value
0
,
1
0,1
0,1 , Then the corresponding generating function item is
(
y
a
2
)
0
+
(
y
a
2
)
1
=
1
+
y
a
2
(y^{a_2})^{0} + (y^{a_2})^{1}= 1+ y^{a_2}
(ya2)0+(ya2)1=1+ya2
⋮
\vdots
⋮
a
n
a_n
an Item corresponds to the generating function item ,
x
n
x_n
xn Value
0
,
1
0,1
0,1 , Then the corresponding generating function item is
(
y
a
n
)
0
+
(
y
a
n
)
1
=
1
+
y
a
n
(y^{a_n})^{0} + (y^{a_n})^{1}= 1+ y^{a_n}
(yan)0+(yan)1=1+yan
Multiply the above generated function items , Then the complete generating function can be obtained :
G
(
x
)
=
(
1
+
y
a
1
)
(
1
+
y
a
2
)
⋯
(
1
+
y
a
n
)
G(x) = (1+ y^{a_1}) (1+ y^{a_2}) \cdots (1+ y^{a_n})
G(x)=(1+ya1)(1+ya2)⋯(1+yan)
After the above generation function is written , Calculation an ,
y
y
y Of
N
N
N Coefficient of power , Namely Positive integer
N
N
N The number of splitting schemes ;
2、 Unordered split Allow repetition
Discuss Unordered split , Repetition is allowed , This way Equivalent to Without restrictions , With coefficients Of Nonnegative integer solutions of indefinite equations The situation of ;
a
1
a_1
a1 Item corresponds to the generating function item ,
x
1
x_1
x1 Value
0
,
1
,
⋯
0,1, \cdots
0,1,⋯ , Then the corresponding generating function item is
(
y
a
1
)
0
+
(
y
a
1
)
1
+
(
y
a
1
)
2
=
1
+
y
a
1
+
y
2
a
1
⋯
(y^{a_1})^{0} + (y^{a_1})^{1} + (y^{a_1})^{2}= 1+ y^{a_1} + y^{2a_1}\cdots
(ya1)0+(ya1)1+(ya1)2=1+ya1+y2a1⋯
a
2
a_2
a2 Item corresponds to the generating function item ,
x
2
x_2
x2 Value
0
,
1
,
⋯
0,1, \cdots
0,1,⋯ , Then the corresponding generating function item is
(
y
a
2
)
0
+
(
y
a
2
)
1
+
(
y
a
2
)
2
=
1
+
y
a
2
+
y
2
a
2
⋯
(y^{a_2})^{0} + (y^{a_2})^{1} + (y^{a_2})^{2}= 1+ y^{a_2} + y^{2a_2}\cdots
(ya2)0+(ya2)1+(ya2)2=1+ya2+y2a2⋯
⋮
\vdots
⋮
a
n
a_n
an Item corresponds to the generating function item ,
x
n
x_n
xn Value
0
,
1
,
⋯
0,1, \cdots
0,1,⋯ , Then the corresponding generating function item is
(
y
a
n
)
0
+
(
y
a
n
)
1
+
(
y
a
n
)
2
=
1
+
y
a
n
+
y
2
a
n
⋯
(y^{a_n})^{0} + (y^{a_n})^{1} + (y^{a_n})^{2}= 1+ y^{a_n} + y^{2a_n}\cdots
(yan)0+(yan)1+(yan)2=1+yan+y2an⋯
Multiply the above generated function items , Then the complete generating function can be obtained :
G
(
x
)
=
(
1
+
y
a
1
+
y
2
a
1
⋯
)
(
1
+
y
a
2
+
y
2
a
2
⋯
)
⋯
(
1
+
y
a
n
+
y
2
a
n
⋯
)
G(x) = (1+ y^{a_1}+ y^{2a_1}\cdots) (1+ y^{a_2} + y^{2a_2}\cdots) \cdots (1+ y^{a_n}+ y^{2a_n}\cdots )
G(x)=(1+ya1+y2a1⋯)(1+ya2+y2a2⋯)⋯(1+yan+y2an⋯)
The above generating function can be generated according to Common values of the following generation functions :
{
a
n
}
\{a_n\}
{ an} ,
a
n
=
1
n
a_n = 1^n
an=1n ;
A
(
x
)
=
∑
n
=
0
∞
x
n
=
1
1
−
x
\begin{aligned} A(x) & = \sum_{n=0}^{\infty} x^n = \frac{1}{1-x} \end{aligned}
A(x)=n=0∑∞xn=1−x1
take
1
+
y
a
1
+
y
2
a
1
⋯
1+ y^{a_1}+ y^{2a_1}\cdots
1+ya1+y2a1⋯ Medium
y
a
1
y^{a_1}
ya1 Yuan Cheng
x
x
x , Then you can get
1
+
x
+
x
2
+
x
3
+
⋯
1 + x + x^2 + x^3 + \cdots
1+x+x2+x3+⋯
The corresponding sequence is
1
n
1^n
1n
As mentioned above
1
+
y
a
1
+
y
2
a
1
⋯
=
1
1
−
y
a
1
1+ y^{a_1}+ y^{2a_1}\cdots =\cfrac{1}{1-y^{a_1}}
1+ya1+y2a1⋯=1−ya11
The final simplification result :
G
(
x
)
=
(
1
+
y
a
1
+
y
2
a
1
⋯
)
(
1
+
y
a
2
+
y
2
a
2
⋯
)
⋯
(
1
+
y
a
n
+
y
2
a
n
⋯
)
G(x) = (1+ y^{a_1}+ y^{2a_1}\cdots) (1+ y^{a_2} + y^{2a_2}\cdots) \cdots (1+ y^{a_n}+ y^{2a_n}\cdots )
G(x)=(1+ya1+y2a1⋯)(1+ya2+y2a2⋯)⋯(1+yan+y2an⋯)
=
1
(
1
−
y
a
1
)
(
1
−
y
a
2
)
⋯
(
1
−
y
a
n
)
\ \ \ \ \ \ \ \ \ \ =\cfrac{1}{ (1-y^{a_1}) (1-y^{a_2}) \cdots (1-y^{a_n}) }
=(1−ya1)(1−ya2)⋯(1−yan)1
After the above generation function is written , Calculation an ,
y
y
y Of
N
N
N Coefficient of power , Namely Positive integer
N
N
N The number of splitting schemes ;
边栏推荐
- PHP MySQL order by keyword
- Talk about the design and implementation logic of payment process
- Line by line explanation of yolox source code of anchor free series network (6) -- mixup data enhancement
- Design limitations of structure type (struct)
- Investigation on the operation prospect of the global and Chinese Anti enkephalinase market and analysis report on the investment strategy of the 14th five year plan 2022-2028
- Leetcode540: a single element in an ordered array
- Lesson 13 of the Blue Bridge Cup -- tree array and line segment tree [exercise]
- 面试官:值为 nil 为什么不等于 nil ?
- Classroom attendance system based on face recognition tkinter+openpyxl+face_ recognition
- Basic grammar of interview (Part 2)
猜你喜欢

Classroom attendance system based on face recognition tkinter+openpyxl+face_ recognition

Bidding procurement scheme management of Oracle project management system
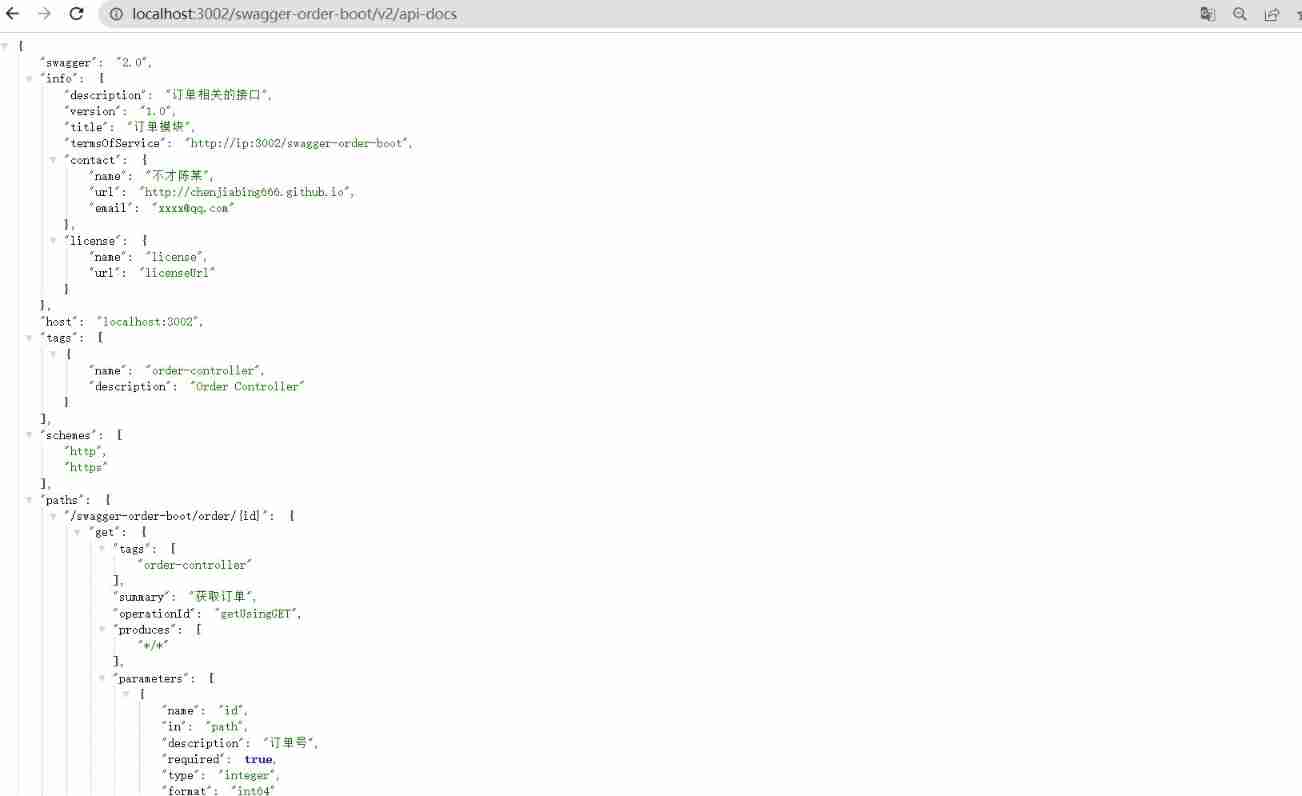
How do microservices aggregate API documents? This wave of operation is too good
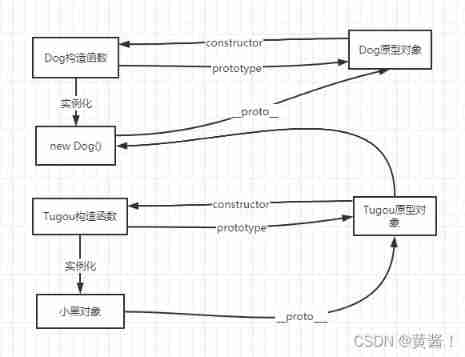
Prototype inheritance..
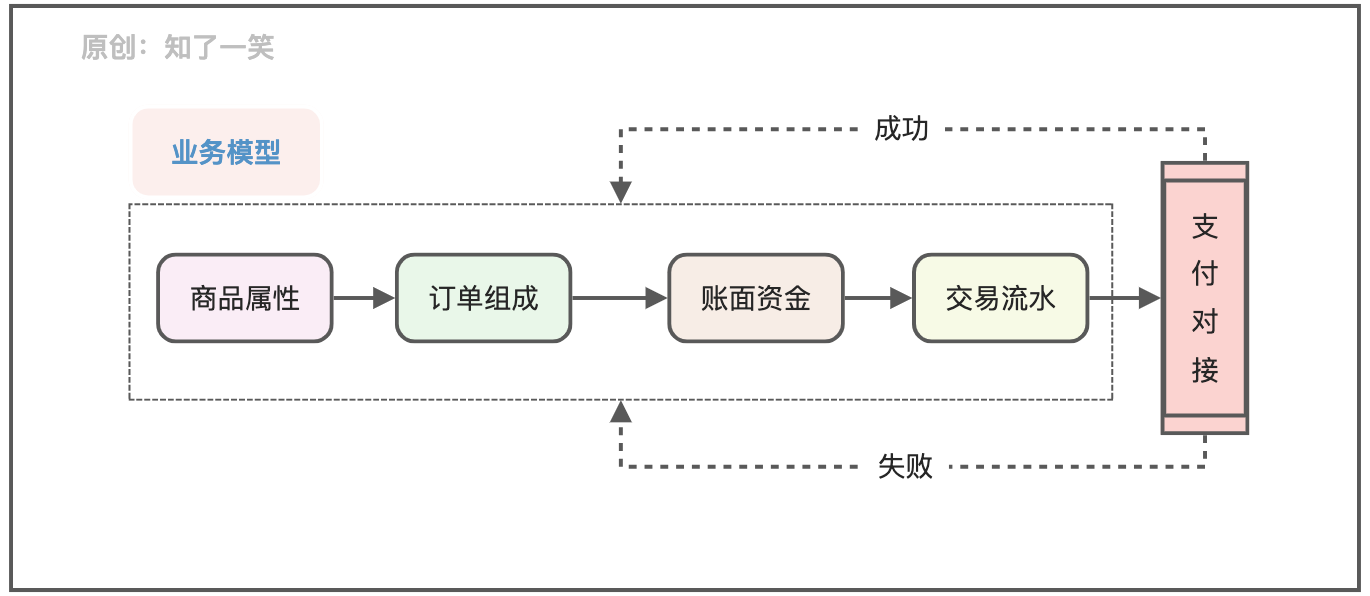
聊聊支付流程的设计与实现逻辑
![[combinatorics] generating function (generating function application scenario | using generating function to solve recursive equation)](/img/e6/9880e708aed42dc82c94aea002020c.jpg)
[combinatorics] generating function (generating function application scenario | using generating function to solve recursive equation)

Investigation on the operation prospect of the global and Chinese Anti enkephalinase market and analysis report on the investment strategy of the 14th five year plan 2022-2028

win32:堆破坏的dump文件分析
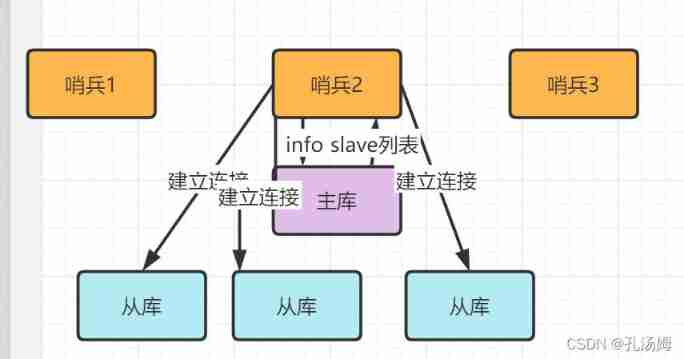
Redis core technology and practice - learning notes (VIII) sentinel cluster: sentinel hung up

Ml (machine learning) softmax function to realize the classification of simple movie categories
随机推荐
Mathematical formula (test)
Computer graduation design PHP makeup sales Beauty shopping mall
ES6类的继承
Research on Swift
ArrayList分析3 : 删除元素
AcWing 271. 杨老师的照相排列【多维DP】
Redis core technology and practice - learning notes (VII) sentinel mechanism
圖像24比特深度轉8比特深度
Talk about the design and implementation logic of payment process
[combinatorics] generating function (property summary | important generating function)*
Win32: analyse du fichier dump pour la défaillance du tas
Distributed task distribution framework gearman
[combinatorics] generating function (linear property | product property)
Leetcode 108 converts an ordered array into a binary search tree -- recursive method
聊聊支付流程的设计与实现逻辑
Redis core technology and practice - learning notes (IX): slicing cluster
Keepalived 设置不抢占资源
Redis on local access server
Computer graduation design PHP campus address book telephone number inquiry system
[combinatorics] generating function (use generating function to solve the number of solutions of indefinite equation example 2 | extended to integer solution)