当前位置:网站首页>On Lagrange interpolation and its application
On Lagrange interpolation and its application
2022-07-03 16:46:00 【Ouye xjx】
Preface
I've been doing for many years NOI The original title is , And then it did [NOI2019] robot , I was surprised to find that I didn't learn Lagrange interpolation !
There was an inserted question in the previous provincial topic ([ Provincial election joint examination 2022] Tree filling ), But in O n e I n D a r k \rm O\red{neInDark} OneInDark Sterling inversion is used under the recommendation of . Actually, pulling and inserting is very simple , And it is more suitable to do things like filling trees 、 Robots are like this DP Optimize the topic .
brief introduction
Stick to others
In numerical analysis , Lagrange interpolation is based on French 18 Century mathematician Joseph · A polynomial interpolation method named by Lagrange . If you observe a physical quantity in practice , The corresponding observations are obtained in several different places , Lagrange interpolation can find a polynomial , It just takes the observed value at each observation point . The above polynomial is called Lagrange ( interpolation ) polynomial .
Lagrange interpolation
as everyone knows , Give a n n n Polynomial of degree n + 1 n+1 n+1 A point value can uniquely find this polynomial , A simple solution is to list n + 1 n+1 n+1 Equation and then use Gauss elimination , Complexity O ( n 3 ) O(n^3) O(n3), It is often accompanied by the problem of accuracy .
Lagrange interpolation can be used in O ( n 2 ) O(n^2) O(n2) Find the polynomial with enough accuracy in time .
Directly up Lagrange interpolation formula :
f ( x ) = ∑ i = 0 n y i ∏ j ≠ i x − x j x i − x j f(x)=\sum_{i=0}^ny_i\prod_{j\neq i}\frac{x-x_j}{x_i-x_j} f(x)=i=0∑nyij=i∏xi−xjx−xj This formula is very clever , Because you can find that it can just get all the point values , And the maximum number is n n n.
Using this formula to directly find polynomials is also O ( n 3 ) O(n^3) O(n3)( It's slower than high consumption ), But it can be optimized !
We can find out g ( x ) = ∏ i = 0 n ( x − x i ) g(x)=\prod_{i=0}^n(x-x_i) g(x)=∏i=0n(x−xi), Then enumeration y i y_i yi First of all O ( n ) O(n) O(n) Calculate the following ∏ j ≠ i 1 x i − x j \prod_{j\neq i}\frac{1}{x_i-x_j} ∏j=ixi−xj1, And then because of g ( x ) g(x) g(x) It was not cut off when calculating , So single ( x − x i ) (x-x_i) (x−xi) Divisibility g ( x ) g(x) g(x), direct O ( n ) O(n) O(n) Recursively find ∏ j ≠ i ( x − x j ) \prod_{j\neq i}(x-x_j) ∏j=i(x−xj) that will do ( Pay attention to special judgment x i = 0 x_i=0 xi=0). In this way, the total complexity is reduced to O ( n 2 ) O(n^2) O(n2).
Find the value of a single point
Here, to find the value of a single point means to give k ∉ { x i ∣ 0 ≤ i ≤ n } k\notin \{x_i|0\le i\le n\} k∈/{ xi∣0≤i≤n}, We need to ask for f ( k ) f(k) f(k).
Obviously, we can directly find f ( x ) f(x) f(x) Then bring in the solution , But when our goal is only to find f ( k ) f(k) f(k) when , Doing so is cumbersome and inefficient .
We might as well bring Lagrange interpolation formula directly :
f ( k ) = ∑ i = 0 n y i ∏ j ≠ i k − x j x i − x j f(k)=\sum_{i=0}^ny_i\prod_{j\neq i}\frac{k-x_j}{x_i-x_j} f(k)=i=0∑nyij=i∏xi−xjk−xj Because it is no longer a polynomial , So we can O ( n ) O(n) O(n) Find all in time ∏ j ≠ i ( k − x j ) \prod_{j\neq i}(k-x_j) ∏j=i(k−xj), Then enumerate each time y i y_i yi Just ask ∏ j ≠ i 1 x i − x j \prod_{j\neq i}\frac{1}{x_i-x_j} ∏j=ixi−xj1 了 . Although still O ( n 2 ) O(n^2) O(n2), But it reduces the constant and is simpler .
O(n) Find the value of a single point
Or just ask f ( k ) f(k) f(k).
In most topics applied to pull and insert , this n + 1 n+1 n+1 A point value satisfies subscript continuity , Or equidistant , namely x 1 − x 0 = x 2 − x 1 = . . . = x n − x n − 1 x_1-x_0=x_2-x_1=...=x_n-x_{n-1} x1−x0=x2−x1=...=xn−xn−1.
At this time, we can do some pretreatment ( For example, when the spacing is equal to 1 When , You need to preprocess the inverse of factorial ), Then you can do it once O ( 1 ) O(1) O(1) Find out ∏ j ≠ i 1 x i − x j \prod_{j\neq i}\frac{1}{x_i-x_j} ∏j=ixi−xj1.( Special attention should be paid to symbols )
application
There's a classic question : Calculation ∑ i = 1 n i k \sum_{i=1}^ni^k ∑i=1nik. This problem can obviously be inversed by Stirling O ( k log k ∼ k 2 ) O(k\log k\sim k^2) O(klogk∼k2) solve .
As we all know, this thing is about n n n Of k + 1 k+1 k+1 Sub polynomial , So we can O ( k ) O(k) O(k)( Ignore fast exponents , You can also use a linear sieve ) Before finding out k + 2 k+2 k+2 A point value , Then use the above method O ( k ) O(k) O(k) Pull and insert n n n Answer at , In this way, the total complexity is only O ( k ) O(k) O(k).
More practical scenarios are in some DP In question , For example, you need to ask m m m individual DP Value to transfer , But you find this m m m A function with a point value is a function with a small number of times n n n Sub polynomial , Then you can just ask for the front n + 1 n+1 n+1 individual DP value , The rest can be pulled and inserted .
Generally, it needs inductive proof to see that this is a polynomial , But I will not
边栏推荐
- (补)双指针专题
- IDEA-配置插件
- Capacités nécessaires à l'analyse des données
- Pytorch 1.12 was released, officially supporting Apple M1 chip GPU acceleration and repairing many bugs
- 浅谈拉格朗日插值及其应用
- Thread pool executes scheduled tasks
- Mysql database -dql
- Explore Netease's large-scale automated testing solutions see here see here
- Aike AI frontier promotion (7.3)
- RF Analyze Demo搭建 Step by Step
猜你喜欢

Arduino esp32: overall framework of lvgl project (I)
TCP congestion control details | 3 design space
MySQL Basics

关于学习Qt编程的好书精品推荐

Idea configuration plug-in
Processing strategy of message queue message loss and repeated message sending
美团一面:为什么线程崩溃崩溃不会导致 JVM 崩溃
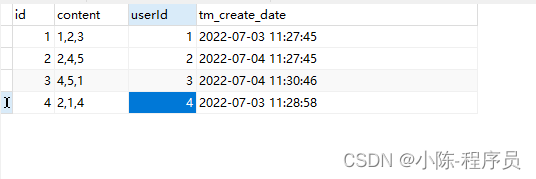
Mysql 将逗号隔开的属性字段数据由列转行
一台服务器最大并发 tcp 连接数多少?65535?

What is the pledge pool and how to pledge?
随机推荐
中南大学|通过探索理解: 发现具有深度强化学习的可解释特征
跟我学企业级flutter项目:简化框架demo参考
利用MySQL中的乐观锁和悲观锁实现分布式锁
Explore Cassandra's decentralized distributed architecture
Top k questions of interview
斑馬識別成狗,AI犯錯的原因被斯坦福找到了
Recommendation of good books on learning QT programming
Data driving of appium framework for mobile terminal automated testing
Summary of three methods of PHP looping through arrays list (), each (), and while
[combinatorics] non descending path problem (number of non descending paths with constraints)
NLP四范式:范式一:非神经网络时代的完全监督学习(特征工程);范式二:基于神经网络的完全监督学习(架构工程);范式三:预训练,精调范式(目标工程);范式四:预训练,提示,预测范式(Prompt工程)
Visual SLAM algorithms: a survey from 2010 to 2016
[combinatorics] recursive equation (outline of recursive equation content | definition of recursive equation | example description of recursive equation | Fibonacci Series)
Custom plug-in construction and use of QT plug-in
CC2530 common registers for port initialization
面试之 top k问题
14 topics for performance interviews between superiors and subordinates (4)
Alibaba P8 painstakingly sorted it out. Summary of APP UI automated testing ideas. Check it out
Basis of target detection (IOU)
Informatics Olympiad all in one YBT 1175: divide by 13 | openjudge noi 1.13 27: divide by 13