Kalman filter -- Derivation from Gaussian fusion

0. introduction

“ If the ancient Greeks knew the normal distribution , There must be a normal goddess in the temple of Olympus , She is in charge of the chaos of the world ！”

1. Bayes' rule

• Another way to deduce , Derivation from the angle of error ？ Refer to the previous derivation . The previous derivation is too cumbersome , It feels more like mathematical derivation , From the perspective of Bayesian rule and Gaussian fusion , The physical meaning is very clear , More easy to understand .
• In one sentence Bayes' rule + Gaussian fusion ： According to Bayes' law, there are , A posteriori estimate $\propto$ likelihood * transcendental , Reference link ; Then according to the assumption （ The error follows Gaussian distribution ）, Through the properties of Gaussian distribution , take Likelihood Gaussian distribution and A priori Gaussian distribution Multiply to get the distribution of a posteriori estimate .

It is enough for this article to read here .

---

The solution of state estimation problem ：

Suppose the system $k$ The observation quantity at the time is $z_k$ , The state quantity is $x_k$ , These two variables are random variables that conform to a certain distribution , And they are not independent of each other . We hope to find out :
$$P\left({\mathbf{x}}_k\mid {\mathbf{x}}_0,{\mathbf{z}}_{1:k}\right)$$
According to the Bayes rule ,( Reference to the probability formula in estimation ) The probability solution of the system state is split as follows :
$$P\left({\mathbf{x}}_k\mid {\mathbf{x}}_0,{\mathbf{z}}_{1:k}\right)\propto P\left({\mathbf{z}}_k\mid {\mathbf{x}}_k\right)P\left({\mathbf{x}}_k\mid {\mathbf{x}}_0,{\mathbf{z}}_{1:k-1}\right)$$

Suppose the system Satisfy Markov properties , namely $x_k$ Only with $x_{K-1}$ relevant , Not related to earlier states （ Here's the picture ）, It can be further simplified to ：

$$P\left({\mathbf{x}}_k\mid {\mathbf{x}}_0,{\mathbf{z}}_{1:k}\right)\propto P\left({\mathbf{z}}_k\mid {\mathbf{x}}_k\right)P\left({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1}\right)$$
among :

• $P\left({\mathbf{z}}_k\mid {\mathbf{x}}_k\right)$ Is the likelihood term , Can be given by the observation equation
• $P\left({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1}\right)$ Is a priori term , It can be derived from the state transition equation

This problem can be solved by filter correlation algorithm , Such as Kalman Filter or Extented Kalman Filter.

---

In state estimation ：

$$p(\mathbf{x}\mid \mathbf{y})=\frac{p(\mathbf{y}\mid \mathbf{x})p(\mathbf{x})}{p(\mathbf{y})}$$

Give the formula physical meaning ：

• $x$ ： state , It can be deduced from the state transition equation , Also known as a priori
• $y$ ： Sensor readings
• $p(y|x)$ : Sensor model , Can be given by the observation equation , Also known as likelihood
• $p(x|y)$ : State estimation , Also known as a posteriori

So Bayesian estimation ： A posteriori estimate $\propto$ likelihood * transcendental . Reference link .

---

2.kalman deduction

Start with an example , Definition $k$ The status of the system at the moment is $x_k$ , Suppose there are two parts: position and speed :

$$x_k=\left[\begin{array}{l}{p}_k\\ v_k\end{array}\right]$$

To further express $x_k$ The uncertainty of each member and the relationship between each dimension , Introduce covariance matrix :

$${\mathbf{P}}_k=\left[\begin{array}{cc}{\Sigma }_{pp}& {\Sigma }_{pv}\\ {\Sigma }_{vp}& {\Sigma }_{vv}\end{array}\right]$$

among :

• ${\Sigma }_{pp}$ and ${\Sigma }_{vv}$ Is the variance of the state component
• ${\Sigma }_{vp}$ and ${\Sigma }_{pv}$ describe $p$ and $v$ Covariance between

Pictured above ( Left ), The relationship between speed and position is independent , Because their variances are not affected by each other ; Diagram ( Right ) On the contrary .

further , It is known that $k-1$ The state of the moment $x_{k-1}$ , We can first predict its motion relationship $k$ The state of the moment $x_k$ .

situation 1: Suppose that the condition of uniform motion is satisfied in a short time :

$${\overline{\mathbf{x}}}_k=\left[\begin{array}{cc}1& \Delta t\\ 0& 1\end{array}\right]{\hat{\mathbf{x}}}_{k-1}={\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}$$

among :

• ${\overline{\mathbf{x}}}_k$ by $k$ A priori distribution of time
• ${\hat{\mathbf{x}}}_{k-1}$ by $k-1$ A posteriori distribution of time
• ${\mathbf{F}}_k$ Is the state transition matrix

situation 2: The above state transition process , It means that the system moves at a constant speed without any external intervention , But imagine what would happen if there were external influences during the exercise ? such as , An artificial push .

$${\overline{\mathbf{x}}}_k={\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}+{\mathbf{B}}_k{\mathbf{u}}_k$$

among :

• ${\mathbf{u}}_k$ Represents external input
• ${\mathbf{B}}_k$ The transformation relation matrix representing external input and system state change

situation 3: In the above system state modeling , Are idealized models , System noise is not considered . To better model the system state transition relationship , We introduce Gaussian noise term to simulate system noise . After considering the noise ${\overline{\mathbf{x}}}_k$ as follows :

$${\overline{\mathbf{x}}}_k={\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}+{\mathbf{B}}_k{\mathbf{u}}_k+{\mathbf{w}}_k\text{\hspace{1em}(1)}$$

among :

• ${\mathbf{w}}_k\sim N\left(0,{\mathbf{Q}}_k\right)$ Gaussian noise

$Cov(x)=\mathbf{\Sigma }$ , According to the properties of covariance matrix :

$$\mathrm{Cov}(\mathbf{A}\mathbf{x})=\mathbf{A}\mathbf{\Sigma }{\mathbf{A}}^T$$ Bayesian rule and Gaussian fusion

For the predicted state , Can be described as :

$$\begin{array}{c}\mathrm{Cov}\left({\hat{\mathbf{x}}}_{k-1}\right)={\hat{\mathbf{P}}}_{k-1}\\ {\overline{\mathbf{x}}}_k={\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}\end{array}\}\Rightarrow \mathrm{Cov}\left({\overline{\mathbf{x}}}_k\right)=\mathrm{Cov}\left({\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}\right)={\mathbf{F}}_k{\hat{\mathbf{P}}}_{k-1}{\mathbf{F}}_k^T$$

That is ：

$${\overline{\mathbf{P}}}_k={\mathbf{F}}_k{\hat{\mathbf{P}}}_{k-1}{\mathbf{F}}_k^T$$

Consider noise ${\overline{\mathbf{x}}}_k$, Its covariance can be recorded as ：

$${\overline{\mathbf{P}}}_k={\mathbf{F}}_k{\hat{\mathbf{P}}}_{k-1}{\mathbf{F}}_k^T+{\mathbf{Q}}_k\text{\hspace{1em}(2)}$$

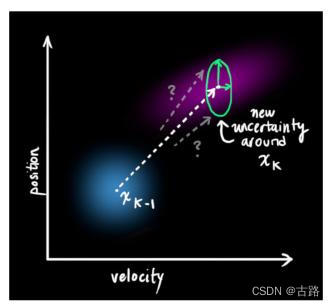
according to $k-1$ The posterior state of time ${\hat{\mathbf{x}}}_{k-1}$, We can predict $k$ A priori state of time ${\overline{\mathbf{x}}}_k$ And its covariance matrix ${\overline{\mathbf{p}}}_k$ :
$${\overline{\mathbf{x}}}_k={\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}+{\mathbf{B}}_k{\mathbf{u}}_k+{\mathbf{w}}_k\text{\hspace{1em}(1)}$$

${\overline{\mathbf{x}}}_k$ Satisfy the following distribution ：

$$N\left({\overline{\mathbf{x}}}_k,{\overline{\mathbf{P}}}_k\right)=N\left({\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}+{\mathbf{B}}_k{\mathbf{u}}_k,{\mathbf{F}}_k{\hat{\mathbf{P}}}_{k-1}{\mathbf{F}}_k^T+{\mathbf{Q}}_k\right)\text{\hspace{1em}(2)}$$

When you get $k$ Systematic measurement of time ${\mathbf{z}}_k$ when , You can try to pass ${\mathbf{z}}_k$ Revise $k$ The posterior state of time ${\hat{\mathbf{x}}}_k$ And its covariance matrix ${\hat{\mathbf{p}}}_k$.

Suppose it is measured by some sensors ${\mathbf{z}}_k=(position,velocity)$ , In this way, we can get the following results ：

$${\mathbf{z}}_k={\overline{\mathbf{x}}}_k$$

In order to further generalize the observation and measurement ${\mathbf{z}}_k$ And state quantity ${\overline{\mathbf{x}}}_k$ The relationship between , Define observation matrix ${\mathbf{H}}_k$:

$${\mathbf{z}}_k={\mathbf{H}}_k{\overline{\mathbf{x}}}_k\text{\hspace{1em}(3)}$$
According to the properties of covariance matrix , It can be deduced that the variance of the observation is :

$$\mathbf{\Sigma }={\mathbf{H}}_k{\overline{\mathbf{P}}}_k{\mathbf{H}}_k^T\text{\hspace{1em}(4)}$$

further , Considering the observed Gaussian noise ${\mathbf{v}}_k$ Satisfy $N(0,{\mathbf{R}}_k)$ Distribution , The following formula can be obtained ：

$${\mathbf{z}}_k={\mathbf{H}}_k{\overline{\mathbf{x}}}_k+{\mathbf{v}}_k\text{\hspace{1em}(5)}$$

${\mathbf{z}}_k$ Satisfy the following distribution ：

$$N\left({\mathbf{z}}_k,\mathbf{\Sigma }\right)=N\left({\mathbf{H}}_k{\overline{\mathbf{x}}}_{\mathbf{k}},{\mathbf{H}}_k{\overline{\mathbf{P}}}_k{\mathbf{H}}_k^T+{\mathbf{R}}_k\right)\text{\hspace{1em}(6)}$$

among , The formula (2) It describes ${\overline{\mathbf{x}}}_k$ The distribution of , The formula (6) It describes ${\mathbf{z}}_k$ The distribution of .

---

Review of Gaussian distribution knowledge ：

The product of two Gaussian distributions is still a Gaussian distribution , And in order to get the distribution function of the overlapping part of two Gaussian distributions , We usually multiply two Gaussian distributions .

$$N\left(x,{\mu }^{\prime },{\sigma }^{\prime }\right)=N\left(x,{\mu }_0,{\sigma }_0\right)\cdot N\left(x,{\mu }_1,{\sigma }_1\right)$$

from $N(x,\mu ,\sigma )=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$ It can be deduced that :

$$\begin{array}{rl}& {\mu }^{\prime }={\mu }_0+\frac{{\sigma }_0^2\left({\mu }_1-{\mu }_0\right)}{{\sigma }_0^2+{\sigma }_1^2}\\ & {\sigma }^{\prime 2}={\sigma }_0^2-\frac{{\sigma }_0^4}{{\sigma }_0^2+{\sigma }_1^2}\end{array}$$

hypothesis $k=\frac{{\sigma }_0^2}{{\sigma }_0^2+{\sigma }_1^2}$, The above formula can be reduced to ：

$$\begin{array}{rl}& {\mu }^{\prime }={\mu }_0+K\left({\mu }_1-{\mu }_0\right)\\ & {\sigma }^{\prime 2}={\sigma }_0^2-K{\sigma }_0^2\end{array}$$

Extend the above formula to multidimensional space :

$$\begin{array}{c}\mathbf{K}={\mathbf{\Sigma }}_0{\left({\mathbf{\Sigma }}_0+{\mathbf{\Sigma }}_1\right)}^{-1}\\ {\mathbf{\mu }}^{\prime }={\mathbf{\mu }}_0+\mathbf{K}\left({\mathbf{\mu }}_1-{\mathbf{\mu }}_0\right)\\ {\mathbf{\Sigma }}^{\prime }={\mathbf{\Sigma }}_0+\mathbf{K}{\mathbf{\Sigma }}_0\end{array}$$

---

go back to kalman deduction

${\bar{\mathbf{x}}}_k$ Satisfy the following distribution ：

$$N\left({\overline{\mathbf{x}}}_k,{\overline{\mathbf{P}}}_k\right)=N\left({\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}+{\mathbf{B}}_k{\mathbf{u}}_k,{\mathbf{F}}_k{\hat{\mathbf{P}}}_{k-1}{\mathbf{F}}_k^T+{\mathbf{Q}}_k\right)\text{\hspace{1em}(2)}$$
${\mathbf{z}}_k$ Satisfy the following distribution :
$$N\left({\mathbf{z}}_k,\Sigma \right)=N\left({\mathbf{H}}_{\mathbf{k}}{\overline{\mathbf{x}}}_{\mathbf{k}},{\mathbf{H}}_k{\overline{\mathbf{P}}}_k{\mathbf{H}}_k^T+{\mathbf{R}}_k\right)\text{\hspace{1em}(6)}$$
take ${\overline{\mathbf{x}}}_k$ and ${\mathbf{z}}_k$ The distribution of is substituted into the above formula （ Gaussian distribution knowledge review inside the multi-dimensional space Gaussian distribution fusion formula ）:
$$\begin{array}{c}{\hat{\mathbf{x}}}_k={\overline{\mathbf{x}}}_k+\mathbf{K}\left({\mathbf{z}}_k-{\overline{\mathbf{x}}}_k\right)\\ {\hat{\mathbf{P}}}_k={\overline{\mathbf{P}}}_k+\mathbf{K}{\overline{\mathbf{P}}}_k\end{array}$$
among , $\mathbf{K}={\overline{\mathbf{P}}}_k{\left({\overline{\mathbf{P}}}_k+\mathbf{\Sigma }\right)}^{-1}$ Is the Kalman gain .

The above is based on historical status and observation , The process of estimating the current position and speed state .

---

When the system is a linear Markov system , Can pass Kalman Filter To solve the fusion problem .
$$\{\begin{array}{c}{\overline{\mathbf{x}}}_{\mathbf{k}}={\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}+{\mathbf{B}}_k{\mathbf{u}}_k+{\mathbf{w}}_k\\ {\mathbf{z}}_k={\mathbf{H}}_k{\overline{\mathbf{x}}}_{\mathbf{k}}+{\mathbf{v}}_k\end{array}k=1,2,\cdots ,N\text{\hspace{1em}(7)}$$
From the state transition equation : $$P\left({\overline{\mathbf{x}}}_{\mathbf{k}}\mid {\mathbf{x}}_0,{\mathbf{u}}_{1:k},{\mathbf{z}}_{1:k-1}\right)=N\left({\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}+{\mathbf{B}}_k{\mathbf{u}}_k,{\mathbf{F}}_k{\hat{\mathbf{P}}}_{k-1}{\mathbf{F}}_k^T+{\mathbf{Q}}_k\right)$$

From the observation equation : $$P\left({\mathbf{z}}_k\mid {\overline{\mathbf{x}}}_{\mathbf{k}}\right)=N\left({\mathbf{H}}_k{\overline{\mathbf{x}}}_{\mathbf{k}},{\mathbf{H}}_k{\overline{\mathbf{P}}}_k{\mathbf{H}}_k^T+{\mathbf{R}}_k\right)$$
notes :

• ${\hat{\mathbf{x}}}_{k-1}$ Express $k-1$ A posteriori state of the system state at any time ;
• ${\hat{\mathbf{P}}}_{k-1}$ Represents the posterior variance of the corresponding state ;
• $\mathbf{Q}$ and $\mathbf{R}$ , respectively, Indicates state and observation noise .

According to the Bayes rule $$P\left({\mathbf{x}}_k\mid {\mathbf{x}}_0,{\mathbf{z}}_{1:k}\right)\propto P\left({\mathbf{z}}_k\mid {\mathbf{x}}_k\right)P\left({\mathbf{x}}_k\mid {\mathbf{x}}_0,{\mathbf{z}}_{1:k-1}\right)$$, take $$P\left({\overline{\mathbf{x}}}_{\mathbf{k}}\mid {\mathbf{x}}_0,{\mathbf{u}}_{1:k},{\mathbf{z}}_{1:k-1}\right)$$ and $$P\left({\mathbf{z}}_k\mid {\overline{\mathbf{x}}}_{\mathbf{k}}\right)$$ Multiply , have to ：
$$N\left({\hat{\mathbf{x}}}_k,{\hat{\mathbf{P}}}_k\right)=N\left({\mathbf{H}}_k{\overline{\mathbf{x}}}_{\mathbf{k}},{\mathbf{H}}_k{\overline{\mathbf{P}}}_k{\mathbf{H}}_k^T+{\mathbf{Q}}_k\right)N\left({\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}+{\mathbf{B}}_k{\mathbf{u}}_k,{\mathbf{F}}_k{\hat{\mathbf{P}}}_{k-1}{\mathbf{F}}_k^T+{\mathbf{R}}_k\right)$$
It can be obtained. , Posterior distribution $N\left({\hat{\mathbf{x}}}_k,{\hat{\mathbf{P}}}_k\right)$ Mean and covariance matrix of ：
$$\begin{array}{c}{\hat{\mathbf{x}}}_k={\overline{\mathbf{x}}}_k+\mathbf{K}\left({\mathbf{z}}_k-{\mathbf{H}}_k{\overline{\mathbf{x}}}_k\right)\\ {\hat{\mathbf{P}}}_k=\left(I-\mathbf{K}{\mathbf{H}}_k\right){\overline{\mathbf{P}}}_k\end{array}$$
among , $\mathbf{K}={\overline{\mathbf{P}}}_k{\mathbf{H}}_k^T{\left({\mathbf{H}}_k{\overline{\mathbf{P}}}_k{\mathbf{H}}_k^T+{\mathbf{Q}}_k\right)}^{-1}$ Is the Kalman gain .

3. summary

The state estimation problem is modeled as ：

$$P\left({\mathbf{x}}_k\mid {\mathbf{x}}_0,{\mathbf{z}}_{1:k}\right)\propto P\left({\mathbf{z}}_k\mid {\mathbf{x}}_k\right)P\left({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1}\right)$$
among :

• $P\left({\mathbf{z}}_k\mid {\mathbf{x}}_k\right)$ Is the likelihood term , Can be given by the observation equation
• $P\left({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1}\right)$ Is a priori term , It can be derived from the state transition equation

In one sentence Bayes' rule + Gaussian fusion ： According to Bayes' law, there are , A posteriori estimate $\propto$ likelihood * transcendental , Reference link ; Then according to the assumption （ The error follows Gaussian distribution ）, Through the properties of Gaussian distribution , take Likelihood Gaussian distribution and A priori Gaussian distribution Multiply to get the distribution of a posteriori estimate .