当前位置:网站首页>Uoj 554 [unr 4] challenges Hamilton [find Hamilton path (adjustment method)]
Uoj 554 [unr 4] challenges Hamilton [find Hamilton path (adjustment method)]
2022-06-11 07:30:00 【Master. Yi】
Title Description
Link
Submit answer questions
Give a digraph , Find the longest path without passing through repeated points and edges , Ensure no double edge self ring .
Topic analysis
Look directly at Official explanation Slightly
After doing a little three staining so that there is no problem with the same color edge , We learned the posture of submitting answer questions : Adjustment method , Find one that doesn't make the answer worse , And it can be adjusted all the time .( If you enter a dead end, start again )
On this question , Is to consider adding edges in random order , Then maintain a set of chains , Consider merging two chains at a time , Or replace an edge .
There are some problems in writing :
Violent judgment will form a ring version :
- It's very slow , Basically, I just finished one test . I found that I didn't judge whether the two points have penetration before walking / The degree of . It becomes very fast to go after judgment .
- run 8,9 It took a long time to reach the point , The first 10 Points stuck 99996 perhaps 99997 I can't move . The discovery is the problem of random numbers , Directly in windows Next use srand(rand()) and random_shuffle(), In this way, there are only 2 15 2^{15} 215 Sort by , It's strange to get out . The correct posture is to use c++11 Of mt19937 And the corresponding shuffle(…) The way , This loop section ( It is said that ) yes 2 19937 − 1 2^{19937}-1 219937−1 Of .
After the change, I still run slowly , So it's changed to LCT edition , But the speed difference is not too big , Running to 99996 After that, I still have to run for a long time (>10min) To get results . contrast The standard schedule of the author Later, I found that I used all the edges to judge every time , And the optimized scale is to compare those with those without entry / The relevant edges of the points of the degree are tested , In this way, when the chain length reaches 9999x Only constant edges need to be tested , Surprisingly fast .
So there are some conclusions : If you run very slowly or are inefficient when submitting answers , Then there must be something wrong / There are some obvious optimizations that don't add , You can't just wait , Think about if there is anything you can improve . The general scale can be solved in a very short time .
in addition , The file opening method in the standard program is also worth learning :
Finally, I put on the one that I didn't run fast Code:
#include<bits/stdc++.h>
#define maxn 100005
#define maxm 300005
using namespace std;
int n,m,id[maxm],X[maxm],Y[maxm],L[maxn],R[maxn];
bool use[maxm]; int cnt;
map<long long,int>edge;
namespace LCT{
int ch[maxn][2],fa[maxn],sum[maxn],v[maxn];
bool rev[maxn];
#define il inline
#define pa fa[x]
il bool isc(int x){
return ch[pa][1]==x;}
il bool isr(int x){
return ch[pa][0]!=x&&ch[pa][1]!=x;}
il void pd(int x){
if(rev[x]){
swap(ch[x][0],ch[x][1]),rev[x]=0;
if(ch[x][0]) rev[ch[x][0]]^=1;
if(ch[x][1]) rev[ch[x][1]]^=1;
}
}
il void pdpath(int x){
if(!isr(x)) pdpath(pa);pd(x);}
il void rot(int x){
int y=fa[x],z=fa[y],c=isc(x);
if(!isr(y)) ch[z][ch[z][1]==y]=x;
(ch[y][c]=ch[x][!c])&&(fa[ch[y][c]]=y);
fa[ch[x][!c]=y]=x,fa[x]=z;
}
il void splay(int x){
pdpath(x);
for(;!isr(x);rot(x))
if(!isr(pa)) rot(isc(pa)==isc(x)?pa:x);
}
il void access(int x){
for(int y=0;x;x=fa[y=x]) splay(x),ch[x][1]=y;
}
il void bert(int x){
access(x),splay(x),rev[x]^=1;
}
il int sert(int x){
access(x),splay(x);
for(;ch[x][0];x=ch[x][0]);
return x;
}
il void link(int x,int y){
bert(x);
fa[x]=y;
}
il void cut(int x,int y){
bert(x),access(y),splay(y);
fa[x]=ch[y][0]=0;
}
il bool check(int x,int y){
bert(x); return sert(y)==x;}
}
using namespace LCT;
mt19937 rnd;
int main()
{
freopen("hamil10.in","r",stdin);
freopen("hamil10.out","w",stdout);
srand(time(0));
scanf("%d%d",&n,&m);
for(int i=1;i<=10;i++) scanf("%*d");
for(int i=1;i<=m;i++) scanf("%d%d",&X[i],&Y[i]),id[i]=i,edge[1ll*X[i]*(n+1)+Y[i]]=i;
for(;cnt<n-1;){
cerr<<cnt<<endl;
//srand(rand());
shuffle(id+1,id+1+m,rnd);
for(int o=1,i;o<=m&&cnt<n-1;o++) if(!use[i=id[o]]){
int x=X[i],y=Y[i];
//cerr<<x<<' '<<y<<endl;
if(R[x]&&L[y]) continue;
if(check(x,y)) continue;
if(!R[x]&&!L[y]) use[i]=1,cnt++,R[x]=y,L[y]=x,link(x,y);
else if(rand()&1){
if(R[x]) L[R[x]]=0,cut(x,R[x]),use[edge[1ll*x*(n+1)+R[x]]]=0,cnt--;
if(L[y]) R[L[y]]=0,cut(L[y],y),use[edge[1ll*L[y]*(n+1)+y]]=0,cnt--;
use[i]=1,cnt++,R[x]=y,L[y]=x,link(x,y);
}
}
}
printf("%d\n",n);
for(int i=1;i<=n;i++) if(!L[i]){
for(int x=i;x;x=R[x]) printf("%d ",x);
return 0;
}
}
边栏推荐
- Crmeb/v4.4 Standard Version open version mall source code applet official account h5+app mall source code
- 【HDU6357】Hills And Valleys(DP)
- 【AtCoder2306】Rearranging(拓扑)
- Create a form whose client area is 800 pixels by 600 pixels
- JVM学习记录(七)——类加载过程与双亲委派模型
- Calculate the day of the week for a specific month, year and day
- P3172 [cqoi2015] data selection (Mobius inversion + Du Jiao sieve)
- C language to write a calculator MVC (very interesting code architecture callback and constructor mode and the use of pointer functions)
- CRMEB/V4.4标准版打通版商城源码小程序公众号H5+App商城源码
- Sdl-2 thread logic
猜你喜欢

Post-processing of ffmpeg miscellaneous notes
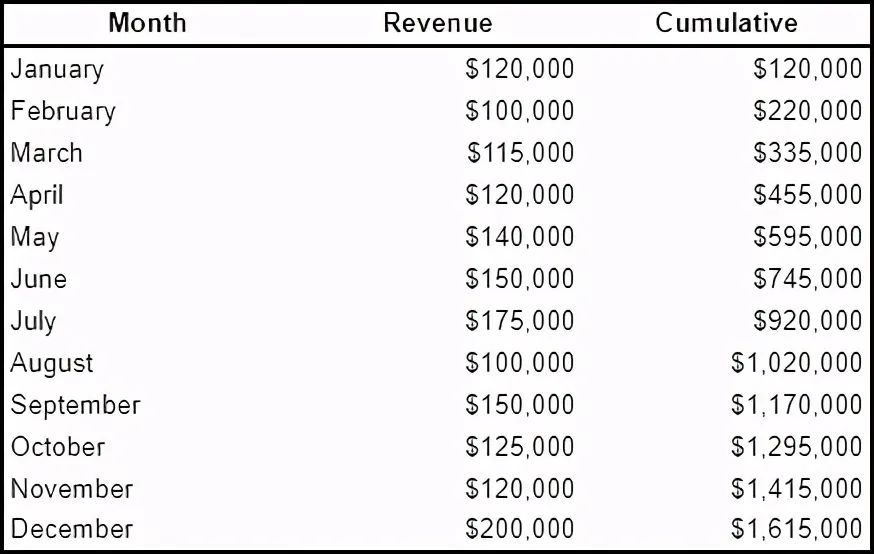
10 advanced concepts that must be understood in learning SQL

【Oracle 数据库】奶妈式教程day04 排序查询

Mistakes in Niuke JS exercise

Several transaction modes of Seata

2022年熔化焊接与热切割考试练习题及答案

【AtCoder2306】Rearranging(拓扑)

Software testing weekly (issue 75): only when you look down, can you see your true self.
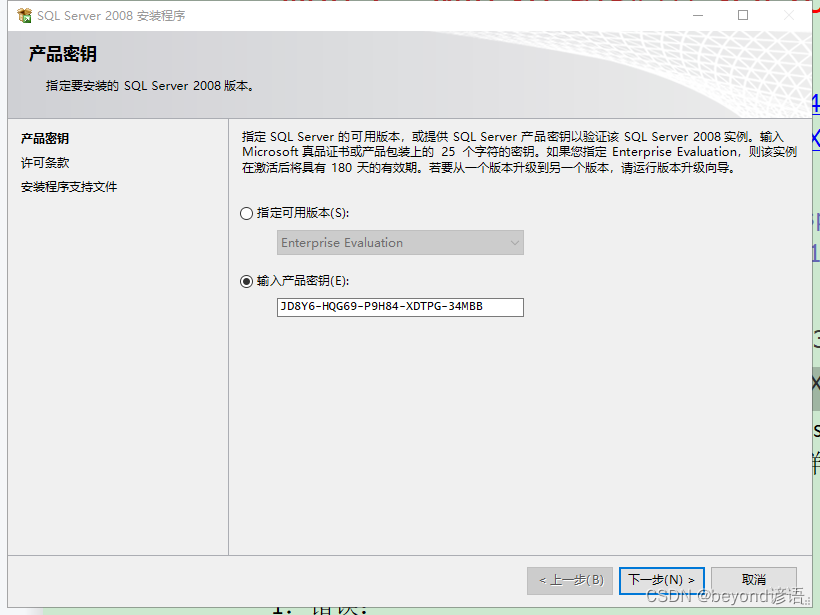
一、SQLServer2008安裝(帶密碼)、創建數據庫、C#窗體項目測試

QT table display data
随机推荐
【CF#223 (Div. 2)】A. Sereja and Dima
Android和iOS逆向分析/安全检测/渗透测试框架
Ffmpe a small demo to understand 80% of common APIs
20200802 T3 I always like [generating function exclusion, Lagrangian inversion]
[Oracle database] mammy tutorial day02 use of database management tool sqlplus
C language volatile
nosqlzoo刷题-1
[analysis of STL source code] summary note (4): behind the scenes hero allocator
2022低压电工操作证考试题模拟考试平台操作
Crmeb/v4.4 Standard Version open version mall source code applet official account h5+app mall source code
[STL source code analysis] summary notes (10): hashtable exploration
2022.5.30-6.5 AI行业周刊(第100期):三年时光
2022 melting welding and thermal cutting exam exercises and answers
Pointer to a two-dimensional array
Qstring to hexadecimal qstring
【AtCoder1998】Stamp Rally(整体二分+并查集)
【CF#697 (Div. 3)】 A - Odd Divisor
big. Js-- use / instance
Console program for viewing BMP files
学 SQL 必须了解的10个高级概念