当前位置:网站首页>Chapter8 支持向量机
Chapter8 支持向量机
2022-07-30 04:16:00 【桑之未落0208】
1 理解支持向量机SVM的原理和目标(what)
1.1 原理
SVM的基本原理时在特征空间中寻找间隔最大化的分离超平面的线性分类器。
- 当训练样本线性可分,通过硬间隔最大化,学习一个线性分类器,即线性可分支持向量机。
- 当训练数据近似线性可分,可引入松弛变量,通过软间隔最大化,学习一个线性分类器,即线性支持向量机。
- 当训练数据线性不可分,通过核函数以及软间隔最大化,学习分线性支持向量机。
1.2 目标
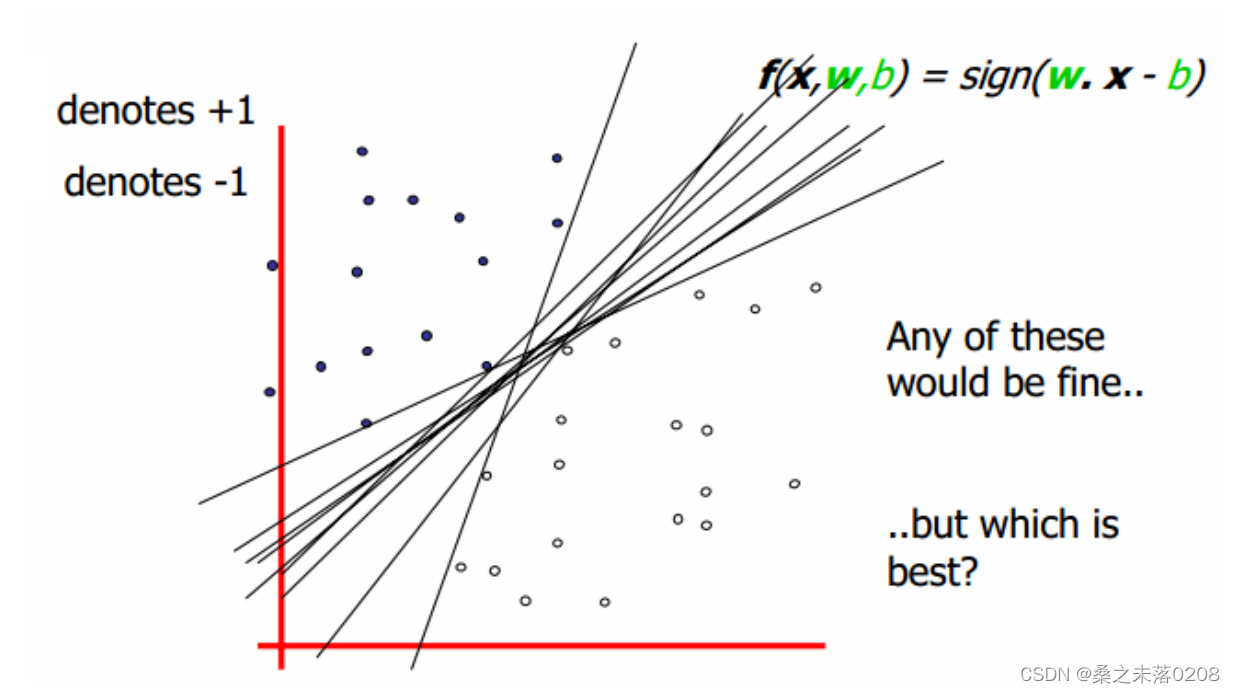
找出所有样本距离无数条线性函数f(x,w,b)最小的距离,再中这些距离中找出最大距离所在的那条直线,即求取w,b的值
如图所示: ,其中
,其中 代表向量。
代表向量。
样本距离该函数之间的距离为:
所以目标为:
2 掌握支持向量机的计算过程和算法步骤(how)
2.1 计算过程
假设给定一个特征空间上的训练数据集 ,其中
,其中 ;
;
 表示为第i个实例(若n大于1,则
表示为第i个实例(若n大于1,则 为向量);
为向量);
 为
为 的类标记,即当
的类标记,即当 时,
时, 为正例,当
为正例,当 时
时 为负例。
为负例。
 称为样本点。
称为样本点。
给定线性可分训练数据集,通过间隔最大化得到的分离超平面为 ,相应的分类决策函数
,相应的分类决策函数 ,该决策函数称为线性可分支持向量机。
,该决策函数称为线性可分支持向量机。
 是某个确定的特征空间转换函数,它的作用是将x映射到(最高的)维度。
是某个确定的特征空间转换函数,它的作用是将x映射到(最高的)维度。
求解分离超平面问题=求解相应的凸二次规划问题。
(1)根据题设 ,有当
,有当 ,
,
从而 。【
。【 为预测值
为预测值  为真实值】
为真实值】
按一定的比例改变w,b(此时超平面的位置不会改变,但可以使得函数间隔改变),则t*y的值同样改变,从而:
 ,其中
,其中 为
为 的
的 范数。
范数。
目标函数:![\underset{w,b}{argmax}\left \{ \frac{1}{||w||}\underset{i}{min} [y_{i}\cdot (w^{T}\cdot \Phi (x_{i})+b)]\right \}](http://img.inotgo.com/imagesLocal/202207/30/202207300416099824_39.gif)
(2)(假如几何距离为B,即 (B为常数)
(B为常数)

等式两边除以B:
 ,此时几何距离变成了1。
,此时几何距离变成了1。

通过等比例缩放w的方法,使得这两类点的函数值都满足 ,即约束条件。
,即约束条件。

(3)因此原问题可以转化为以下问题:
约束条件——
原目标函数——![\underset{w,b}{argmax}\left \{ \frac{1}{||w||}\underset{i}{min} [y_{i}\cdot (w^{T}\cdot \Phi (x_{i})+b)]\right \}](http://img.inotgo.com/imagesLocal/202207/30/202207300416099824_39.gif)
新目标函数—— ,即
,即 ,即
,即
(4)所用方法:拉格朗日乘子法
设函数
原问题是极小极大问题:
原问题的对偶问题是极大极小问题:
然后分别对 求偏导,令其为0:
求偏导,令其为0:


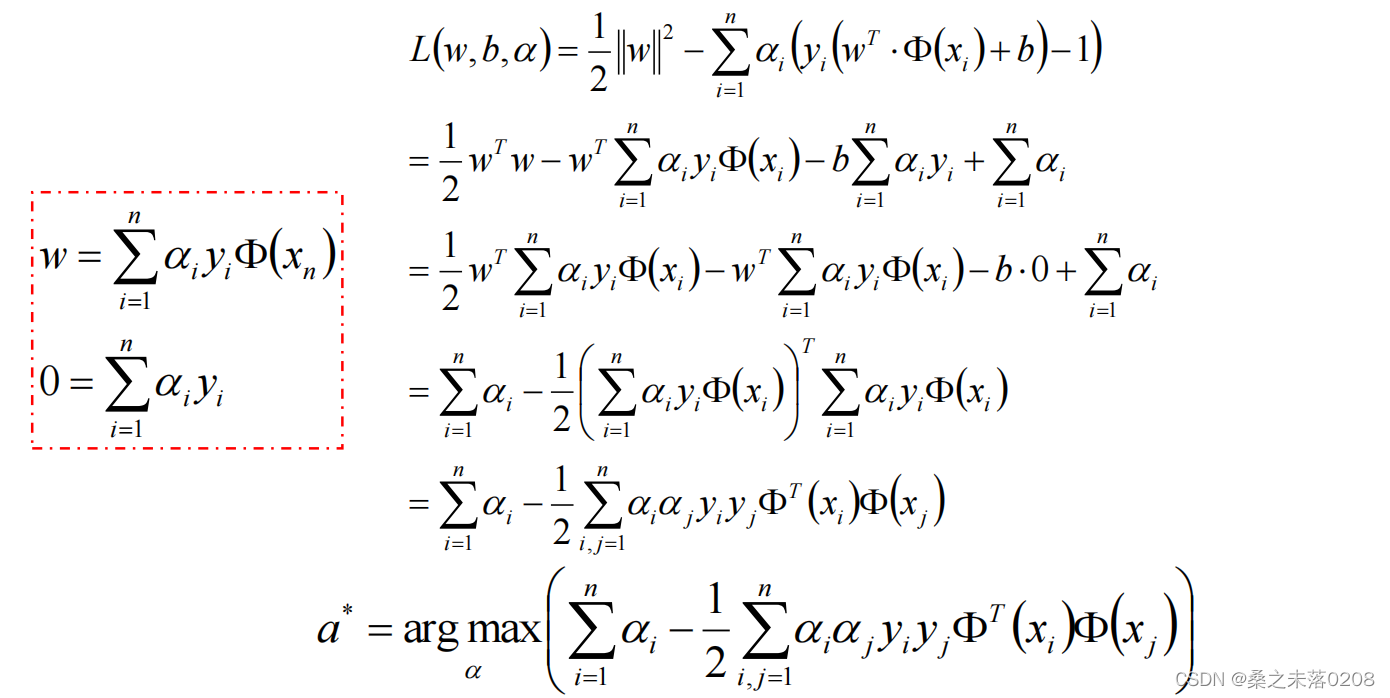
即在 约束条件下求解:
约束条件下求解:

添加负号变为求解:
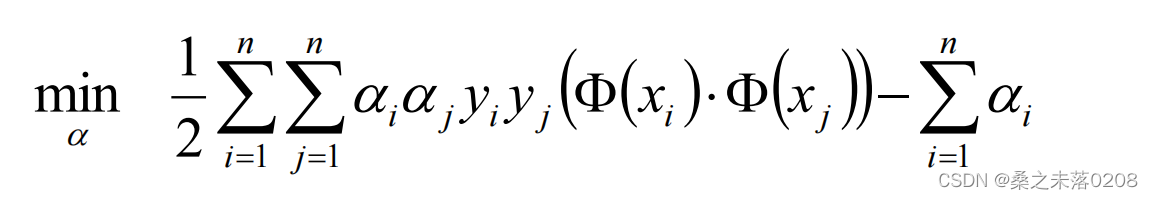

2.2 举例说明

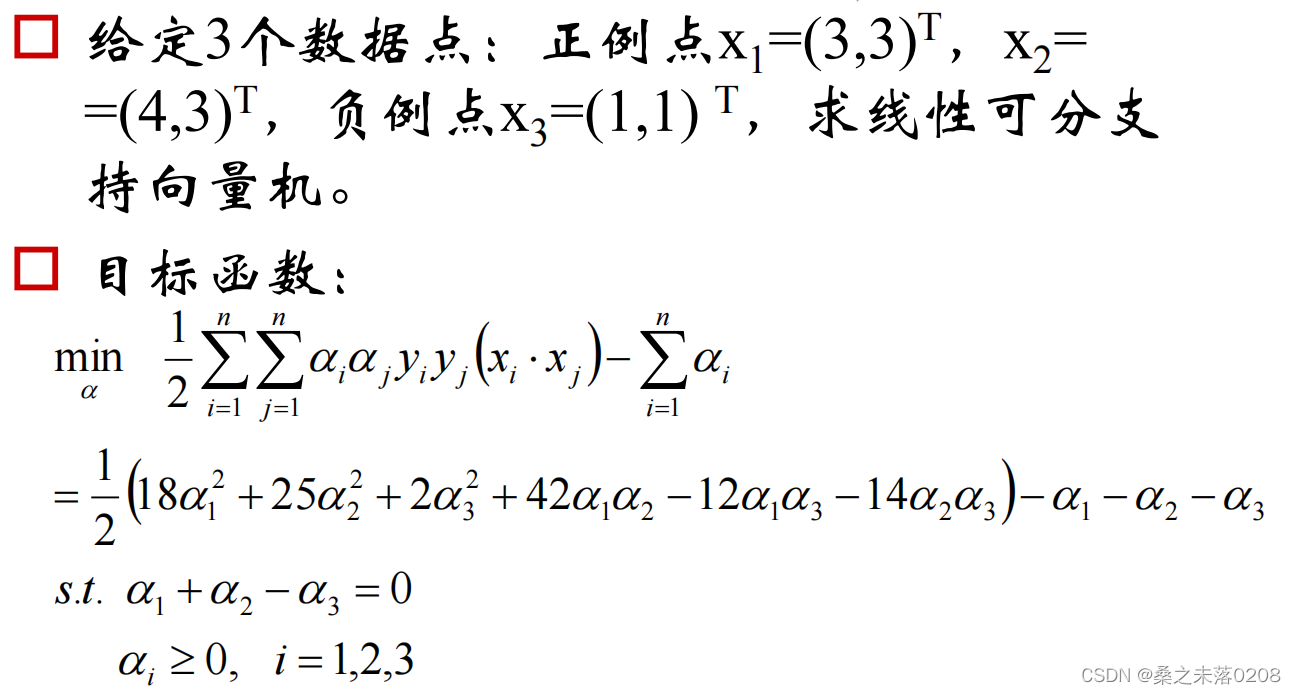

 我们可以看到
我们可以看到  ,则
,则 为非支持向量。
为非支持向量。
2.3 拉格朗日乘子法
约束条件: ,
,
目标:
构造函数: ,其中
,其中 任意值。
任意值。
所以
 (原始问题)
(原始问题)
对偶函数为 
所以接下来对 求导,使其为0。
求导,使其为0。
3 理解软间隔最大化的含义
当训练数据近似线性可分,可增加松弛变量 ,通过软间隔最大化,使得汉化间隔加上松弛变量大于等于1,这样约束条件就变成了
,通过软间隔最大化,使得汉化间隔加上松弛变量大于等于1,这样约束条件就变成了 ,而目标函数就变为
,而目标函数就变为
C小则过渡带越宽,所以有泛化能力。C大时,为了目标函数最小,实际上需要使得 ,即变成线性可分。
,即变成线性可分。
所以:带松弛因子的SVM拉格朗日函数如下:




ps:实际上损失函数为
边栏推荐
- 2022.7.29-----leetcode.593
- 在麒麟V10操作系统上安装MySQL数据库
- Android Studio 实现登录注册-源代码 (连接MySql数据库)
- Pytorch framework learning record 5 - the use of DataLoader
- The difference between forward and redirect
- Mysql version upgrade, copy the Data file directly, the query is very slow
- WEB 渗透之信息收集
- Many overseas authoritative media hotly discuss TRON: laying the foundation for the decentralization of the Internet
- 【Redis高手修炼之路】Jedis——Jedis的基本使用
- MySQL String Concatenation - Various String Concatenation Practical Cases
猜你喜欢
随机推荐
厦门感芯科技MC3172(1):介绍和环境搭建
05全局配置文件application.properties详解
handler+message【消息机制】
Taobao H5 interface to obtain app data 6.0 format
Go 学习笔记(84)— Go 项目目录结构
What are Redis server startup after the operation?
Pytorch framework to study record 6 - the torch. Nn. The Module and the torch nn. Functional. The use of conv2d
Redis server启动后会做哪些操作?
新型LaaS协议Elephant Swap给ePLATO提供可持续溢价空间
sql statement - how to query data in another table based on the data in one table
数组和结构体
Roperties class configuration file & DOS to view the host network situation
golang八股文整理(持续搬运)
How does the Snapdragon 7 series chip perform?Reno8 Pro proves a new generation of God U
Data Lake: Data Integration Tool DataX
SQL Server data type conversion function cast () and convert () explanation
宇宙的尽头是银行?聊聊在银行做软件测试的那些事
【翻译】Envoy Fundamentals,这是一个培训课程,使人们能够更快地采用Envoy Proxy。...
代码开源设计实现思路
Pytorch框架学习记录4——数据集的使用(torchvision.dataset)