当前位置:网站首页>E - Distance Sequence (prefix and optimized dp
E - Distance Sequence (prefix and optimized dp
2022-08-05 00:22:00 【__Rain】
E - Distance Sequence
思路:
d p [ i ] [ j ] dp[i][j] dp[i][j] 表示考虑前 i i i 个数,最后一个数为 j j j 时的方案数
显然 d p [ i ] [ j ] + = d p [ i − 1 ] [ l ] dp[i][j]+=dp[i-1][l] dp[i][j]+=dp[i−1][l], l l l 为前 i − 1 i-1 i−1 个数中以 l l l End and with j j j In the case of the joint method
j − l ≥ k j-l\geq k j−l≥k,即 1 ≤ l ≤ j − k 1\leq l \leq j-k 1≤l≤j−k
l − j ≥ k l-j\geq k l−j≥k,即 j + k ≤ l ≤ m j+k \leq l \leq m j+k≤l≤m
Obviously a prefix and optimization can be maintained
(Note that special judgment is required K = 0 K=0 K=0 的情况
code:
#include<bits/stdc++.h>
#define endl '\n'
#define ll long long
#define ull unsigned long long
#define ld long double
#define all(x) x.begin(), x.end()
#define mem(x, d) memset(x, d, sizeof(x))
#define eps 1e-6
using namespace std;
const int maxn = 2e6 + 9;
const int mod = 998244353;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
ll n, m;
ll dp[1009][5009];
void work()
{
int k;
cin >> n >> m >> k;
if(k == 0){
ll ans = 1;
for(int i = 1; i <= n; ++i)
ans = ans * m % mod;
cout << ans;
return;
}
vector <ll> sum(m + 1, 0);
for(int i = 1; i <= m; ++i) {
dp[1][i] = 1;
sum[i] = sum[i-1] + dp[1][i];
}
for(int i = 2; i <= n; ++i){
vector <ll> now_sum(m + 1, 0);
for(int j = 1; j <= m; ++j){
if(j - k >= 1)
(dp[i][j] += sum[j - k]) %= mod;
//for(int l = 1; l <= j - k; ++l)
// (dp[i][j] += dp[i-1][l]) %= mod;
if(j + k <= m)
(dp[i][j] += (sum[m] - sum[j+k-1] + mod) % mod) %= mod;
//for(int l = j + k; l <= m; ++l)
// (dp[i][j] += dp[i-1][l]) %= mod;
}
for(int j = 1; j <= m; ++j) now_sum[j] = (now_sum[j-1] + dp[i][j]) % mod;
sum = now_sum;
}
cout << sum[m];
}
int main()
{
ios::sync_with_stdio(0);
// int TT;cin>>TT;while(TT--)
work();
return 0;
}
改进 d p dp dp The process does not need to be judged individually,But also think about it k = = 0 k==0 k==0 the situation,Then modify the transfer equation
code:
#include<bits/stdc++.h>
#define endl '\n'
#define ll long long
#define ull unsigned long long
#define ld long double
#define all(x) x.begin(), x.end()
#define mem(x, d) memset(x, d, sizeof(x))
#define eps 1e-6
using namespace std;
const int maxn = 2e6 + 9;
const int mod = 998244353;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
ll n, m, k;
ll dp[1009][5009];
void work()
{
cin >> n >> m >> k;
vector <ll> sum(m + 1, 0);
for(int i = 1; i <= m; ++i) {
dp[1][i] = 1;
sum[i] = sum[i-1] + dp[1][i];
}
for(int i = 2; i <= n; ++i){
vector <ll> now_sum(m + 1, 0);
for(int j = 1; j <= m; ++j){
int l = max(1ll, j - k + 1), r = min(m, j + k - 1);
if(k){
dp[i][j] = (sum[m] - (sum[r] - sum[l-1]) + mod) % mod;
}
else {
dp[i][j] = sum[m];
}
}
for(int j = 1; j <= m; ++j) now_sum[j] = (now_sum[j-1] + dp[i][j]) % mod;
sum = now_sum;
}
cout << sum[m];
}
int main()
{
ios::sync_with_stdio(0);
// int TT;cin>>TT;while(TT--)
work();
return 0;
}
想到 k = 0 k=0 k=0 Then change the transfer equation,I can't do it for a chicken like me,Hence the following writing,It can be completely ignored K K K 的值了,Just make sure every transfer is legal(也就是 r > = l − 1 r>=l-1 r>=l−1)
code:
#include<bits/stdc++.h>
#define endl '\n'
#define ll long long
#define ull unsigned long long
#define ld long double
#define all(x) x.begin(), x.end()
#define mem(x, d) memset(x, d, sizeof(x))
#define eps 1e-6
using namespace std;
const int maxn = 2e6 + 9;
const int mod = 998244353;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
ll n, m, k;
ll dp[1009][5009];
// 考虑前i个数,最后一个数为j
void work()
{
cin >> n >> m >> k;
vector <ll> sum(m + 1, 0);
for(int i = 1; i <= m; ++i) {
// 单独一个数1-m都可以
dp[1][i] = 1;
sum[i] = sum[i-1] + dp[1][i];
}
for(int i = 2; i <= n; ++i){
vector <ll> now_sum(m + 1, 0);
for(int j = 1; j <= m; ++j){
int l = max(1ll, j - k + 1), r = min(m, j + k - 1);// 不合法的区间
dp[i][j] = sum[m];
if(r >= l - 1) {
// If the illegal interval exists, it needs to be deleted
dp[i][j] = (dp[i][j] - (sum[r] - sum[l-1]) + mod) % mod;
}
}
for(int j = 1; j <= m; ++j) now_sum[j] = (now_sum[j-1] + dp[i][j]) % mod;
sum = now_sum;
}
cout << sum[m];
}
int main()
{
ios::sync_with_stdio(0);
// int TT;cin>>TT;while(TT--)
work();
return 0;
}
边栏推荐
- [230]连接Redis后执行命令错误 MISCONF Redis is configured to save RDB snapshots
- 【论文笔记】—低照度图像增强—Unsupervised—EnlightenGAN—2019-TIP
- 【云原生--Kubernetes】调度约束
- "No title"
- More than 2022 cattle school training topic Link with the second L Level Editor I
- 2022牛客多校训练第二场 J题 Link with Arithmetic Progression
- 软件测试面试题:黑盒测试、白盒测试以及单元测试、集成测试、系统测试、验收测试的区别与联系?
- 2022杭电多校第三场 L题 Two Permutations
- 电子行业MES管理系统的主要功能与用途
- 电赛必备技能___定时ADC+DMA+串口通信
猜你喜欢

Essential knowledge for entry-level 3D game modelers
【Valentine's Day special effects】--Canvas realizes full screen love
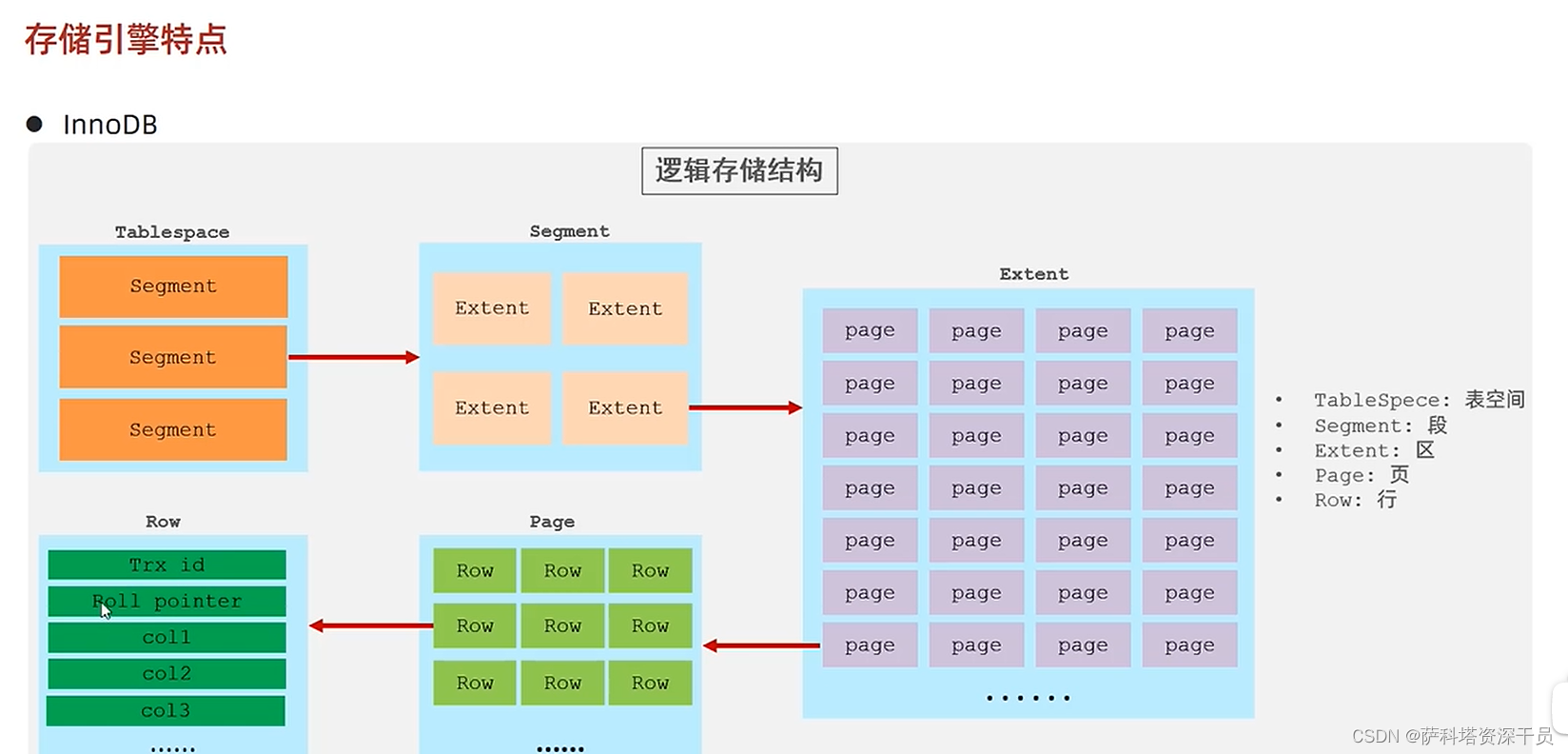
Mysql_14 存储引擎
MongoDB permission verification is turned on and mongoose database configuration

Senior game modelers tell newbies, what are the necessary software for game scene modelers?

数据类型及输入输出初探(C语言)
node使用redis

简单的顺序结构程序(C语言)
QSunSync Qiniu cloud file synchronization tool, batch upload

元宇宙:未来我们的每一个日常行为是否都能成为赚钱工具?
随机推荐
动态上传jar包热部署
canvas 高斯模糊效果
软件测试面试题:您如何看待软件过程改进?在您曾经工作过的企业中,是否有一些需要改进的东西呢?您期望的理想的测试人员的工作环境是怎样的?
ansible学习笔记分享-含剧本示例
tiup update
E - Many Operations (bitwise consideration + dp thought to record the result after the operation
[Cloud Native--Kubernetes] Pod Controller
【LeetCode】Summary of Two Pointer Problems
SV 类的虚方法 多态
[idea] idea configures sql formatting
typeScript - Partially apply a function
Three tips for you to successfully get started with 3D modeling
2022牛客多校训练第二场 H题 Take the Elevator
克服项目管理中恐惧心理
2022杭电多校第三场 L题 Two Permutations
leetcode: 266. All Palindromic Permutations
软件测试面试题:什么是软件测试?软件测试的目的与原则?
E - Many Operations (按位考虑 + dp思想记录操作后的结果
找不到DiscoveryClient类型的Bean
leetcode经典例题——单词拆分