当前位置:网站首页>[mathematical logic] predicate logic (individual word | individual domain | predicate | full name quantifier | existence quantifier | predicate formula | exercise)
[mathematical logic] predicate logic (individual word | individual domain | predicate | full name quantifier | existence quantifier | predicate formula | exercise)
2022-07-03 03:13:00 【Programmer community】
List of articles
- One . Predicate logic related concepts
- 1. Individual words
- 2. The predicate
- 3. quantifiers
- ( 1 ) Full name quantifier
- ( 2 ) There are quantifiers
- Two . Proposition symbolization skill
- 1. Two basic formulas ( important )
- ( 1 ) There is a quality F The individual of All have properties G
- ( 2 ) Existing nature F It also has nature G The individual of
- 2. Propositional symbolization skills
- ( 1 ) Propositional Symbolization Method
- ( 2 ) Problem solving skills
- ( 3 ) If and only if Predicate logic method
- 3. Predicate formula definition
- 3、 ... and . Proposition symbolization exercises
- 1. Simple quantifier Example
- ( 1 ) Examples of full quantifiers
- ( 2 ) Full name quantifier Example 2
- ( 3 ) There is quantifiers Example
- 2. The position of quantifiers is different Resulting symbolization The results are different
- 3. belt perhaps Of Proposition symbolization
- ( 1 ) belt perhaps Of Proposition symbolization
- ( 2 ) belt Or the proposition Example 2
- 4. Complex proposition Example
- ( 1 ) Symbolization of complex propositions
- ( 2 ) Individual domain changes situation Of Two kinds of analysis
- ( 3 ) If and only if Transformation problem
- ( 4 ) Use Full name quantifier and There are quantifiers Two forms Make propositional symbolization
One . Predicate logic related concepts
1. Individual words
individual brief introduction :
- 1. individual source : First order predicate logic in , take Atomic proposition Divide into The subject and Predicate , Here we have Individual words And The predicate Of Concept ;
- 2. individual Concept : take Independent object , Concrete things , Abstract things ( Concept ) be called individual or Individual words ;
- 3. individual Argument : Use
a
,
b
,
c
a,b,c
a,b,c Represents an individual argument ;
- 4. individual Changyuan : Use
x
,
y
,
z
x, y, z
x,y,z Represents individual constant ;
- 5. Individual domain Concept : individual Argument The value of be called Individual domain ;
- 6. Individual domain Value : Individual domain Sure Value Finite set or Infinite set ;
- 7. Total individual domain : Everything in the universe Composed of Individual domain be called Total individual domain ;
A proposition is a statement , The declarative sentence is composed of The subject , Predicate , The object form , The subject object is the individual , Predicate is predicate ;
Predicate logic from individual , The predicate , quantifiers form ;
2. The predicate
The predicate brief introduction :
- 1. Predicate concept : Will represent Individual nature or Relationship between each other Of word be called The predicate ;
- 2. The predicate indicates : Use
F
,
G
,
H
F, G, H
F,G,H Representation predicate Changyuan or Argument ;
- 3. The individual property predicate indicates :
F
(
x
)
F(x)
F(x) Express
x
x
x have nature
F
F
F , Such as
F
(
x
)
F(x)
F(x) Express
x
x
x It's black ;
- 4. Examples of relational property predicates :
F
(
x
,
y
)
F(x, y)
F(x,y) Express
x
,
y
x, y
x,y have Relationship F , Such as :
F
F
F
G
(
x
,
y
)
G(x, y)
G(x,y) Express
x
x
x Greater than
y
y
y ;
3. quantifiers
( 1 ) Full name quantifier
Full name quantifier :Any Medium A Upside down ;
- 1. Language correspondence : Corresponding Natural language in “ arbitrarily ” , “ be-all ” , “ every last ” etc. ;
- 2. Representation : Using symbols
∀
\forall
∀ Express ;
- 3. Reading 1 :
∀
x
\forall x
∀x Represents the individual domain be-all
x
x
x ;
- 4. Reading 2 :
∀
x
(
F
(
x
)
)
\forall x( F(x) )
∀x(F(x)) Express , All in the individual domain
x
x
x All have properties
F
F
F ;
( 2 ) There are quantifiers
There are quantifiers :Exist Medium E Turn left and right, then turn upside down ;
- 1. Language correspondence : Corresponding Natural language in “ There is one ” , “ There is a ” , “ yes , we have ” etc. ;
- 2. Representation : Using symbols
∃
\exist
∃ Express ;
- 3. Reading 1 :
∃
x
\exist x
∃x Represents the individual domain There are
x
x
x ;
- 4. Reading 2 :
∃
x
(
F
(
x
)
)
\exist x( F(x) )
∃x(F(x)) Express , In the individual domain There is
x
x
x Have the quality of
F
F
F ;
Two . Proposition symbolization skill
1. Two basic formulas ( important )
( 1 ) There is a quality F The individual of All have properties G
In the individual domain all There is a quality
F
F
F Of individual , all have nature
G
G
G ;
Use predicate logic to express :
①
F
(
x
)
F(x)
F(x) :
x
x
x Have the quality of
F
F
F ;
②
G
(
x
)
G(x)
G(x) :
x
x
x Have the quality of
G
G
G ;
③ The proposition is symbolized as :
∀
x
(
F
(
x
)
→
G
(
x
)
)
\forall x ( F(x) \rightarrow G(x) )
∀x(F(x)→G(x))
( 2 ) Existing nature F It also has nature G The individual of
Individual domain in Existence has nature
F
F
F At the same time, it has the nature of
G
G
G The individual of ;
Use predicate logic to express :
①
F
(
x
)
F(x)
F(x) :
x
x
x Have the quality of
F
F
F ;
②
G
(
x
)
G(x)
G(x) :
x
x
x Have the quality of
G
G
G ;
③ The proposition is symbolized as :
∃
x
(
F
(
x
)
∧
G
(
x
)
)
\exist x ( F(x) \land G(x) )
∃x(F(x)∧G(x))
2. Propositional symbolization skills
( 1 ) Propositional Symbolization Method
Propositional Symbolization Method :
- 1. Write individual fields : The first Individual domain Write clearly , namely indicate
∀
x
\forall x
∀x , representative Everything , If it's everything , Then it must be indicated that it is the total individual domain ;
- 2. Write a relationship The predicate : Use
F
,
G
,
H
F , G , H
F,G,H indicate Individual nature or Relationship ;
- 3. Propositional symbols : take Proposition symbolization result Indicate the , It's best to bring a detailed explanation ;
( 2 ) Problem solving skills
from Full name quantifier or There are quantifiers Individual words The predicate Combined Predicate logic , You can also think of it as One Predicate logic
F
(
x
)
F(x)
F(x) or
G
(
x
,
y
)
G(x, y)
G(x,y) parts Combine again ;
as follows Predicate logic :
∀
x
(
F
(
x
)
→
∀
y
(
G
(
y
)
→
H
(
x
,
y
)
)
)
\forall x (F(x) \rightarrow \forall y ( G(y) \rightarrow H(x,y) ))
∀x(F(x)→∀y(G(y)→H(x,y)))
among
∀
y
(
G
(
y
)
→
H
(
x
,
y
)
)
\forall y ( G(y) \rightarrow H(x,y) )
∀y(G(y)→H(x,y)) It's already assembled Predicate logic , Now think of it as a nature , perhaps Predicate logic unit
A
A
A , Combine again more complex and Gigantic Predicate logic , Get the following :
∀
x
(
F
(
x
)
→
A
)
\forall x (F(x) \rightarrow A)
∀x(F(x)→A)
therefore , Above Predicate logic After deployment , You get the first
∀
x
(
F
(
x
)
→
∀
y
(
G
(
y
)
→
H
(
x
,
y
)
)
)
\forall x (F(x) \rightarrow \forall y ( G(y) \rightarrow H(x,y) ))
∀x(F(x)→∀y(G(y)→H(x,y)))
( 3 ) If and only if Predicate logic method
If and only if Predicate logic Symbolic method :
If and only if Predicate logic Symbolization :
1> The third variable : Make sure to introduce The third party The variable of ;2> nature or Relationship positive Deduce : The general pattern is
① For allx
x
x And There is a
y
y
y Yes A certain quality or relationship ,
② For allx
x
x and be-all
z
z
z There is a certain nature or relationship ;
③y
y
y And
z
z
z Having equal attributes ;
3> nature or Relationship Back to back : The general pattern is :
① For allx
x
x And There is a
y
y
y Yes A certain quality or relationship ,
②y
y
y And be-all
z
z
z There is another property or Relationship , Generally equal or Unequal Relationship ,
③ Can be launchedx
x
x and
z
z
z Yes perhaps No, some nature or Relationship ;
3. Predicate formula definition
Predicate formula definition :
- 1. The original predicate formula :
n
n
n element The predicate It's a Predicate formula ;
- 2. Negative form : If
A
A
A It's a predicate formula , that
(
¬
A
)
(\lnot A)
(¬A) It's also a predicate formula ;
- 3. Two predicate formulas Combine : If
A
,
B
A, B
(
A
∧
B
)
,
(
A
∨
B
)
,
(
A
→
B
)
,
(
A
B
)
(A \land B) , (A \lor B), (A \rightarrow B), (A \leftrightarrow B)
A,B It's a predicate formula , that
(A∧B),(A∨B),(A→B),(AB) Four kinds of connectives Combined symbols , It's also a predicate formula ;
- 4. Predicate formula And quantifiers Combine : If
A
A
A It's a predicate formula , And it contains Individual variables
x
x
x
x
x Not limited by quantifiers , that
∀
x
A
(
x
)
\forall x A(x)
∀xA(x) , or
∃
x
A
(
x
)
\exist x A(x)
x , And
∃xA(x) It's also a predicate formula ;
- 5. Finite repetitions : A limited number of times Yes Predicate formula Use 1. ~ 4. Methods to deal with Got It's also Predicate formula ;
Predicate formula assembly :
1> After several times assemble Good combination The predicate formula of , perhaps Just written Single Predicate formula , Sure As primitive Predicate formulaS
S
S ;
2> stay The original predicate formulaS
S
S front add
¬
\lnot
¬ It's also a predicate formula , Notice the parentheses on the outside ; ( After combination This predicate formula can be regarded as the original predicate formula
S
S
S Use )
3> Use Conjunctions take Two The original predicate formulaS
S
S Connect , Whole Combine It's also Predicate formula ;( After combination This predicate formula can be regarded as the original predicate formula
S
S
S Use )
4> stay The original predicate formulaS
S
S front add Quantifier constraints
∀
x
A
(
x
)
\forall x A(x)
∀xA(x) , or
∃
x
A
(
x
)
\exist x A(x)
∃xA(x) , After combination It's also Predicate formula ;( After combination This predicate formula can be regarded as the original predicate formula
S
S
S Use )( Be careful Premise : Add quantifier constraints Individual words Can not be There are quantifier constraints )
4> step Of Be careful :
① Premise : The individual in this predicate , Not bound by quantifiers , If there is Constraints cannot be repeated ;
3、 ... and . Proposition symbolization exercises
1. Simple quantifier Example
( 1 ) Examples of full quantifiers
subject :
- 1. requirement : Proposition symbolization :
- 2. Proposition content : Everyone eats ;
① Individual domain : Total individual domain ;
② Related nature or Relationship The predicate Definition :
- 1>
F
(
x
)
F(x)
F(x) :
x
x
x Is the person ;
- 2>
G
(
x
)
G(x)
G(x) :
x
x
x having dinner ;
③ Proposition symbolization :
∀
x
(
F
(
x
)
→
G
(
x
)
)
\forall x (F(x) \rightarrow G(x))
∀x(F(x)→G(x))
( 2 ) Full name quantifier Example 2
subject :
- 1. requirement : Proposition symbolization :
- 2. Proposition content : All the students in a class have studied calculus ;
① Individual domain : Total individual domain ;
② Related nature or Relationship The predicate Definition :
- 1>
F
(
x
)
F(x)
F(x) :
x
x
x Is a class of students ;
- 2>
G
(
x
)
G(x)
G(x) :
x
x
x Studied calculus ;
③ Proposition symbolization :
∀
x
(
F
(
x
)
→
G
(
x
)
)
\forall x (F(x) \rightarrow G(x))
∀x(F(x)→G(x))
( 3 ) There is quantifiers Example
subject :
- 1. requirement : Proposition symbolization :
- 2. Proposition content : Some people like sugar ;
answer :
① Individual domain : Total individual domain ;
② Related nature or Relationship The predicate Definition :
- 1>
F
(
x
)
F(x)
F(x) :
x
x
x Is the person ;
- 2>
G
(
x
)
G(x)
G(x) :
x
x
x Like sugar ;
③ Proposition symbolization :
∃
x
(
F
(
x
)
∧
G
(
x
)
)
\exist x (F(x) \land G(x))
∃x(F(x)∧G(x))
Another symbolic method : Sugar can also be called an individual :
① Individual domain : Total individual domain
② The predicate : nature / Relationship Definition :
F
(
x
)
F(x)
F(x) Express
x
x
x Is the person
G
(
y
)
G(y)
G(y) Express
y
y
y It's sugar
H
(
x
,
y
)
H(x, y)
H(x,y) Express
x
x
x Like to eat
y
y
y
③ Proposition symbolization :
∃
x
(
F
(
x
)
∧
G
(
x
)
∧
H
(
x
,
y
)
)
\exist x (F(x) \land G(x) \land H(x, y))
∃x(F(x)∧G(x)∧H(x,y))
2. The position of quantifiers is different Resulting symbolization The results are different
subject :
- 1. requirement : Proposition symbolization :
- 2. Proposition content : Men run faster than women ;
1> The way One :
① Individual domain : Total individual domain ;
② Related nature or Relationship The predicate Definition :
- 1>
F
(
x
)
F(x)
F(x) :
x
x
x It's men ;
- 2>
G
(
y
)
G(y)
G(y) :
y
y
y It's a woman ;
- 3>
H
(
x
,
y
)
H(x,y)
H(x,y) :
x
x
x Than
y
y
y Run fast ;
③ Proposition symbolization :
∀
x
(
F
(
x
)
→
∀
y
(
G
(
y
)
→
H
(
x
,
y
)
)
)
\forall x (F(x) \rightarrow \forall y ( G(y) \rightarrow H(x,y) ))
∀x(F(x)→∀y(G(y)→H(x,y)))
The propositional symbol has an equivalent form :
∀
x
∀
y
(
F
(
x
)
∧
G
(
y
)
→
H
(
x
,
y
)
)
)
\forall x \forall y (F(x) \land G(y) \rightarrow H(x,y) ))
∀x∀y(F(x)∧G(y)→H(x,y)))
This proposition is false , But it does not prevent us from symbolizing it ;
Symbolic analysis :
① take∀
y
(
G
(
y
)
→
H
(
x
,
y
)
)
\forall y ( G(y) \rightarrow H(x,y) )
∀y(G(y)→H(x,y)) Independent analysis , First Whole Propositions are all in
∀
x
\forall x
∀x Scope , here Has the following properties , All women , All men run faster than women ; Think of it as an independent proposition
A
A
A ;
② The following analysis∀
x
(
F
(
x
)
→
A
)
∀x(F(x)→ A)
∀x(F(x)→A) , For all men Come on , As long as it's a man , There are proposition
A
A
A The nature of ;
2> The way Two :
① Individual domain : Total individual domain ;
② Related nature or Relationship The predicate Definition :
- 1>
F
(
x
)
F(x)
F(x) :
x
x
x It's men ;
- 2>
G
(
x
)
G(x)
G(x) :
x
x
x It's a woman ;
- 3>
H
(
x
,
y
)
H(x,y)
H(x,y) :
x
x
x Than
y
y
y Run fast ;
③ Proposition symbolization :
∀
x
∀
y
(
F
(
x
)
∧
G
(
x
)
→
H
(
x
,
y
)
)
\forall x \forall y (F(x) \land G(x) \rightarrow H(x,y))
∀x∀y(F(x)∧G(x)→H(x,y))
This proposition is false , But it does not prevent us from symbolizing it ;
Symbolic analysis :
takeF
(
x
)
∧
G
(
x
)
F(x) \land G(x)
F(x)∧G(x) As a whole
A
A
A , namely
x
x
x It's men ,
y
y
y It's a woman , For all
x
,
y
x, y
x,y There is a quality
A
A
A , that
x
,
y
x, y
x,y At the same time, it has properties or Relationship
H
(
x
,
y
)
H(x,y)
H(x,y) ;
3. belt perhaps Of Proposition symbolization
( 1 ) belt perhaps Of Proposition symbolization
subject :
- 1. requirement : Proposition symbolization :
- 2. Proposition content : Every student in a class has a computer perhaps He has a friend who owns a computer ;
answer :
① Individual domain : All the students in a class
② Individual nature or Relationship Predicate definition :
- 1>
F
(
x
)
F(x)
F(x) :
x
x
x There's a computer ;
- 2>
G
(
x
,
y
)
G(x, y)
G(x,y) :
x
x
x and
y
y
y It's a friend. ;
③ Propositional symbols :
∀
x
(
F
(
x
)
∨
∃
y
(
F
(
y
)
∧
G
(
x
,
y
)
)
)
\forall x ( F(x) \lor \exist y ( F(y) \land G(x , y) ) )
∀x(F(x)∨∃y(F(y)∧G(x,y)))
analysis :
1> Individual domain definition : Individual domain As the “ All the students in a class ” ;2> The outermost quantifier is determined : They all have properties “ Every student in a class has a computer perhaps He has a friend who owns a computer ” , therefore The outermost layer has to be Full name quantifier
∀
x
(
A
(
x
)
)
\forall x (A(x))
∀x(A(x)) , Now let's start to analyze
A
(
x
)
A(x)
A(x) ;
3> Between the two properties is perhaps The relationship between : Two properties are used
∨
\lor
∨ Connect , Namely
B
(
x
)
B(x)
B(x) ( “ There's a computer ” ) and
C
(
x
)
C(x)
C(x) ( “ There is a friend who has a computer ” ) , Current symbols :
∀
x
(
B
(
x
)
∧
C
(
x
)
)
\forall x (B(x) \land C(x))
∀x(B(x)∧C(x)) ;
4> “ There's a computer ” : Expressed as
F
(
x
)
F(x)
F(x) ; Current symbols :
∀
x
(
F
(
x
)
∧
C
(
x
)
)
\forall x (F(x) \land C(x))
∀x(F(x)∧C(x)) ;
5> “ There is a friend with a computer ” ( This is more complicated ) :
① First Make up One Studenty
y
y , This
y
y
y On behalf of the friend who has a computer ;
② Then determine the quantifier :" There is one " Obviously, there are quantifiers∃
y
\exist y
∃y ( If you use full weighing words , Everyone in that class is his friend ) ;
③ For this Fictitiousy
y
y The requirement is ,
y
y
y Two conditions are met at the same time , “a. There are computers ” “b.
x
,
y
x,y
x,y It's a friend. ” , Therefore use
∧
\land
∧ Connect them , Finally expressed as
F
(
y
)
∧
G
(
x
,
y
)
F(y) \land G(x , y)
F(y)∧G(x,y) ;
④ The symbol of this sentence is :∃
y
(
F
(
y
)
∧
G
(
x
,
y
)
)
\exist y ( F(y) \land G(x , y) )
∃y(F(y)∧G(x,y)) ;
6> The final symbol is :
∀
x
(
F
(
x
)
∨
∃
y
(
F
(
y
)
∧
G
(
x
,
y
)
)
)
\forall x ( F(x) \lor \exist y ( F(y) \land G(x , y) ) )
∀x(F(x)∨∃y(F(y)∧G(x,y))) ;
( 2 ) belt Or the proposition Example 2
Proposition symbolization :
In a class Every Student perhaps been Beijing , Or have been Shanghai
answer :
Proposition symbolization result :
① Individual domain : All students in a class
② Individual nature or Relationship Predicate definition :
- 1>
F
(
x
)
F(x)
F(x) :
x
x
x Have been to Beijing ;
- 2>
G
(
x
)
G(x)
G(x) :
x
x
x Have been to Shanghai ;
③ Propositional symbols :
∀
x
(
F
(
x
)
∨
G
(
x
)
)
\forall x ( F(x) \lor G(x))
∀x(F(x)∨G(x))
analysis :
1> Individual domain quantifiers analysis :
∀
x
\forall x
∀x refer to All of a class Student Medium every last , be-all Student ;
2>
F
(
x
)
∨
G
(
x
)
F(x) \lor G(x)
F(x)∨G(x) Reading : Express
x
x
x been Beijing perhaps been Shanghai ;
3>
∀
x
(
F
(
x
)
∨
G
(
x
)
)
\forall x ( F(x) \lor G(x))
∀x(F(x)∨G(x)) Reading : All the students , Or have been to Beijing , Or have been to Shanghai , One of them must be chosen , And You can only choose one ;
4. Complex proposition Example
( 1 ) Symbolization of complex propositions
subject :
- 1. requirement : Proposition symbolization :
- 2. Proposition content : There is a student
x
x
x, For all two different students
y
y
y and
z
z
z Come on , If
x
x
x And
y
y
y It's a good friend , also
x
x
x and
z
z
z It's also a good friend , that
y
y
y and
z
z
z Not a good friend ;
Topic analysis :
- 1. Individual domain analysis : The individuals involved in the proposition are Student , that take Individual domain Set to All the students ;
- 2. Nature and relationship analysis :
- ① “ For all two different students ” : It's about Two different students , Therefore need Define a The predicate , Express The two students are Different or same ;
- ② "
x
x
x And
y
y
y It's a good friend " : involves Two Student yes perhaps No A good friend , therefore Here we need to define a predicate , Express Two students yes perhaps No A good friend ;
- 3. Topic frame analysis :
- ① Quantifier constraints : " There is a student
x
x
x, For all two different students
y
y
y and
z
z
∃
x
∀
y
∀
z
\exist x \forall y \forall z
∃x∀y∀z , Then I'm right
x
,
y
,
z
x, y , z
z Come on " You can write The outermost Of Quantifier constraints ,
x,y,z Describe the relationship between ;
- ② " If
x
x
x And
y
y
y It's a good friend , also
x
x
x and
z
z
z It's also a good friend , that
y
y
y and
z
z
- a> proposition
A
A
x
x
x And
y
y
y It's a good friend , also
x
x
x and
z
z
z It's also a good friend " ,
A :" If
- b> proposition
B
B
y
y
y and
z
z
z Not a good friend " ;
B :" that
- c> proposition
A
,
B
A,B
A
→
B
A \rightarrow B
A→B ;
A,B The relationship between :
z Not a good friend ; " : This proposition It can be used implication Conjunctions To said ;
- a> proposition
- ① Quantifier constraints : " There is a student
answer :
Proposition symbolization result :
① Individual domain : All the students
② Individual nature or Relationship Predicate definition :
- 1>
F
(
x
,
y
)
F(x, y)
F(x,y) :
x
x
x and
y
y
y It's a good friend ;
- 2>
G
(
x
,
y
)
G(x, y)
G(x,y) :
x
x
x and
y
y
y It's the same ;
③ Propositional symbols :
∃
x
∀
y
∀
z
(
(
¬
G
(
y
,
z
)
∧
F
(
x
,
y
)
∧
F
(
x
,
z
)
)
→
¬
F
(
y
,
z
)
)
\exist x \forall y \forall z ( ( \lnot G(y, z) \land F(x,y) \land F(x, z) ) \rightarrow \lnot F(y, z) )
∃x∀y∀z((¬G(y,z)∧F(x,y)∧F(x,z))→¬F(y,z))
analysis :
1> Quantifier analysis :
∃
x
∀
y
∀
z
\exist x \forall y \forall z
∃x∀y∀z Corresponding In the title " There is a student
x
x
x, For all two different students
y
y
y and
z
z
z Come on "
2>
(
¬
G
(
y
,
z
)
∧
F
(
x
,
y
)
∧
F
(
x
,
z
)
)
( \lnot G(y, z) \land F(x,y) \land F(x, z) )
(¬G(y,z)∧F(x,y)∧F(x,z)) analysis : This sentence corresponds to “ Two different students
y
y
y and
z
z
z Come on , If
x
x
x And
y
y
y It's a good friend , also
x
x
x and
z
z
z It's also a good friend ” At the same time satisfy this Three conditions ;
3>
¬
F
(
y
,
z
)
\lnot F(y, z)
¬F(y,z) analysis : Corresponding to the result “ that
y
y
y and
z
z
z Not a good friend ” ;
4> At the same time satisfy 3 Conditions Then exit the result :
(
¬
G
(
y
,
z
)
∧
F
(
x
,
y
)
∧
F
(
x
,
z
)
)
→
¬
F
(
y
,
z
)
( \lnot G(y, z) \land F(x,y) \land F(x, z) ) \rightarrow \lnot F(y, z)
(¬G(y,z)∧F(x,y)∧F(x,z))→¬F(y,z) ;
5> Add quantifier constraints Get the final result :
∃
x
∀
y
∀
z
(
(
¬
G
(
y
,
z
)
∧
F
(
x
,
y
)
∧
F
(
x
,
z
)
)
→
¬
F
(
y
,
z
)
)
\exist x \forall y \forall z ( ( \lnot G(y, z) \land F(x,y) \land F(x, z) ) \rightarrow \lnot F(y, z) )
∃x∀y∀z((¬G(y,z)∧F(x,y)∧F(x,z))→¬F(y,z)) ;
( 2 ) Individual domain changes situation Of Two kinds of analysis
subject :
- 1. requirement : Proposition symbolization :
- 2. Proposition content : In a class Some students have been to Beijing
answer :
( 1 ) Method One ( Individual domain by All students in a class ) :
Proposition symbolization result :
① Individual domain : All students in a class
② Individual nature or Relationship Predicate definition :
- 1>
F
(
x
)
F(x)
F(x) :
x
x
x Have been to Beijing ;
③ Propositional symbols :
∃
x
(
F
(
x
)
)
\exist x ( F(x) )
∃x(F(x))
analysis : Just write it directly , Some students , Use There are quantifiers
∃
x
\exist x
∃x Express ,
∃
x
(
F
(
x
)
)
\exist x( F(x) )
∃x(F(x)) Express Some students have been to Beijing ;
( 1 ) Method Two ( Individual domain by Total individual domain ) :
Proposition symbolization result :
① Individual domain : Total individual domain
② Individual nature or Relationship Predicate definition :
- 1>
F
(
x
)
F(x)
F(x) :
x
x
x Have been to Beijing ;
- 2>
G
(
x
)
G(x)
G(x) :
x
x
x Is a class of students ;
③ Propositional symbols :
∃
x
(
F
(
x
)
∧
G
(
x
)
)
\exist x ( F(x) \land G(x))
∃x(F(x)∧G(x))
analysis :
∃
x
(
F
(
x
)
∧
G
(
x
)
)
\exist x ( F(x) \land G(x))
∃x(F(x)∧G(x))
1> Individual domain analysis : Individual domain by Total individual domain , that
∃
x
\exist x
∃x Namely There is something , The attribute of this thing is something in the universe ;
2>
F
(
x
)
∧
G
(
x
)
F(x) \land G(x)
F(x)∧G(x) : Sure Reading by There is something , That is, students in a class , Have been to Beijing ;
3> Complete interpretation of :
∃
x
(
F
(
x
)
∧
G
(
x
)
)
\exist x ( F(x) \land G(x))
∃x(F(x)∧G(x)) , Sure Reading by There is something , That is, students in a class , Have been to Beijing ;
( 3 ) If and only if Transformation problem
subject :
- 1. requirement : Proposition symbolization :
- 2. Proposition content : Everyone has only one good friend
answer :
Proposition symbolization result :
① Individual domain : All of you
② Individual nature or Relationship Predicate definition :
- 1>
F
(
x
,
y
)
F(x , y)
F(x,y) :
x
,
y
x , y
x,y It's a good friend ;
- 2>
G
(
x
,
y
)
G(x, y)
G(x,y) :
x
,
y
x , y
x,y equal ;
③ Propositional symbols One :
∀
x
∃
y
∀
z
(
(
F
(
x
,
y
)
∧
¬
G
(
y
,
z
)
)
→
¬
F
(
x
,
z
)
)
\forall x \exist y \forall z ( ( F(x,y) \land \lnot G(y, z) ) \rightarrow \lnot F(x,z) )
∀x∃y∀z((F(x,y)∧¬G(y,z))→¬F(x,z))
analysis : Everyone has only one good friend , here
x
,
y
x ,y
x,y Already a good friend , If there is one
z
z
z And
y
y
y It's not equal , that
x
,
z
x,z
x,z Must not be a good friend ;
Quantifier analysis :
For allx
x
x , There is one.
y
y
y It's his friend , be-all
z
z
z And
x
x
x It's a good friend , that This
z
z
z Namely
y
y
y ;
④ Propositional symbol two :
∀
x
∃
y
∀
z
(
(
F
(
x
,
y
)
∧
F
(
x
,
z
)
)
→
G
(
y
,
z
)
)
\forall x \exist y \forall z ( ( F(x,y) \land F(x, z) ) \rightarrow G(y,z) )
∀x∃y∀z((F(x,y)∧F(x,z))→G(y,z))
analysis : Everyone has only one good friend , If
x
,
y
x,y
x,y It's a good friend ,
x
,
z
x,z
x,z It's a good friend , that
y
,
z
y,z
y,z Definitely equal ;
Quantifier analysis :
For allx
x
x , There is one.
y
y
y It's his friend , be-all
z
z
z And
x
x
x It's a good friend , that This
z
z
z Namely
y
y
y ;
If and only if Predicate logic Symbolic method :
If and only if Predicate logic Symbolization :
1> The third variable : Make sure to introduce The third party The variable of ;2> nature or Relationship positive Deduce : The general pattern is
① For allx
x
x And There is a
y
y
y Yes A certain quality or relationship ,
② For allx
x
x and be-all
z
z
z There is a certain nature or relationship ;
③y
y
y And
z
z
z Having equal attributes ;
3> nature or Relationship Back to back : The general pattern is :
① For allx
x
x And There is a
y
y
y Yes A certain quality or relationship ,
②y
y
y And be-all
z
z
z There is another property or Relationship , Generally equal or Unequal Relationship ,
③ Can be launchedx
x
x and
z
z
z Yes perhaps No, some nature or Relationship ;
( 4 ) Use Full name quantifier and There are quantifiers Two forms Make propositional symbolization
subject :
- 1. requirement : Proposition symbolization :
- 2. Proposition content : Not all animals are cats
answer :
Proposition symbolization result ( The whole quantifier ) : This way Belong to Positive answer ;
① Individual domain : Total individual domain Everything in the universe
② Individual nature or Relationship Predicate definition :
- 1>
F
(
x
)
F(x)
F(x) :
x
x
x yes animal ;
- 2>
G
(
x
)
G(x)
G(x) :
x
x
x yes cat ;
③ Propositional symbols One :
¬
(
∀
x
(
F
(
x
)
→
G
(
x
)
)
)
\lnot ( \forall x ( F(x) \rightarrow G(x) ) )
¬(∀x(F(x)→G(x)))
analysis : Proposition is “ Not all animals are cats ” , Here we begin to disassemble the proposition :
1> Extract negation : Extract the non by¬
\lnot
¬ , The negative proposition is “ Not all animals are cats ” ;
2> Write “ Not all animals are cats ” proposition : namely Anything of animal nature , All have yes cat The nature of , Here, it is symbolized as∀
x
(
F
(
x
)
→
G
(
x
)
)
\forall x ( F(x) \rightarrow G(x) )
∀x(F(x)→G(x)) ;
3> final result :¬
(
∀
x
(
F
(
x
)
→
G
(
x
)
)
)
\lnot ( \forall x ( F(x) \rightarrow G(x) ) )
¬(∀x(F(x)→G(x))) ;
Proposition symbolization result ( There are quantifiers ) : This way Belong to Answer sideways ;
Transforming propositions : There are some animals It's not a cat ;
① Individual domain : Total individual domain Everything in the universe
② Individual nature or Relationship Predicate definition :
- 1>
F
(
x
)
F(x)
F(x) :
x
x
x yes animal ;
- 2>
G
(
x
)
G(x)
G(x) :
x
x
x yes cat ;
③ Propositional symbols One :
∃
x
(
F
(
x
)
∧
¬
G
(
x
)
)
\exist x ( F(x) \land \lnot G(x) )
∃x(F(x)∧¬G(x))
∃
x
(
F
(
x
)
∧
¬
G
(
x
)
)
\exist x ( F(x) \land \lnot G(x) )
∃x(F(x)∧¬G(x)) analysis : There is something , Its satisfaction is the nature of animals , At the same time satisfy It's not a cat The nature of ;
边栏推荐
- Update and return document in mongodb - update and return document in mongodb
- Left connection, inner connection
- docker安装redis
- VS 2019 配置tensorRT生成engine
- Change cell color in Excel using C - cell color changing in Excel using C
- MySQL practice 45 [global lock and table lock]
- Thunderbolt Chrome extension caused the data returned by the server JS parsing page data exception
- Spark on yarn资源优化思路笔记
- Sous - système I2C (IV): débogage I2C
- The idea setting code is in UTF-8 idea Properties configuration file Chinese garbled
猜你喜欢

Creation and destruction of function stack frame
I2C subsystem (II): I3C spec
Unity3d RPG implementation (medium)
分布式事务
Hi3536C V100R001C02SPC040 交叉编译器安装
Deep reinforcement learning for intelligent transportation systems: a survey paper reading notes
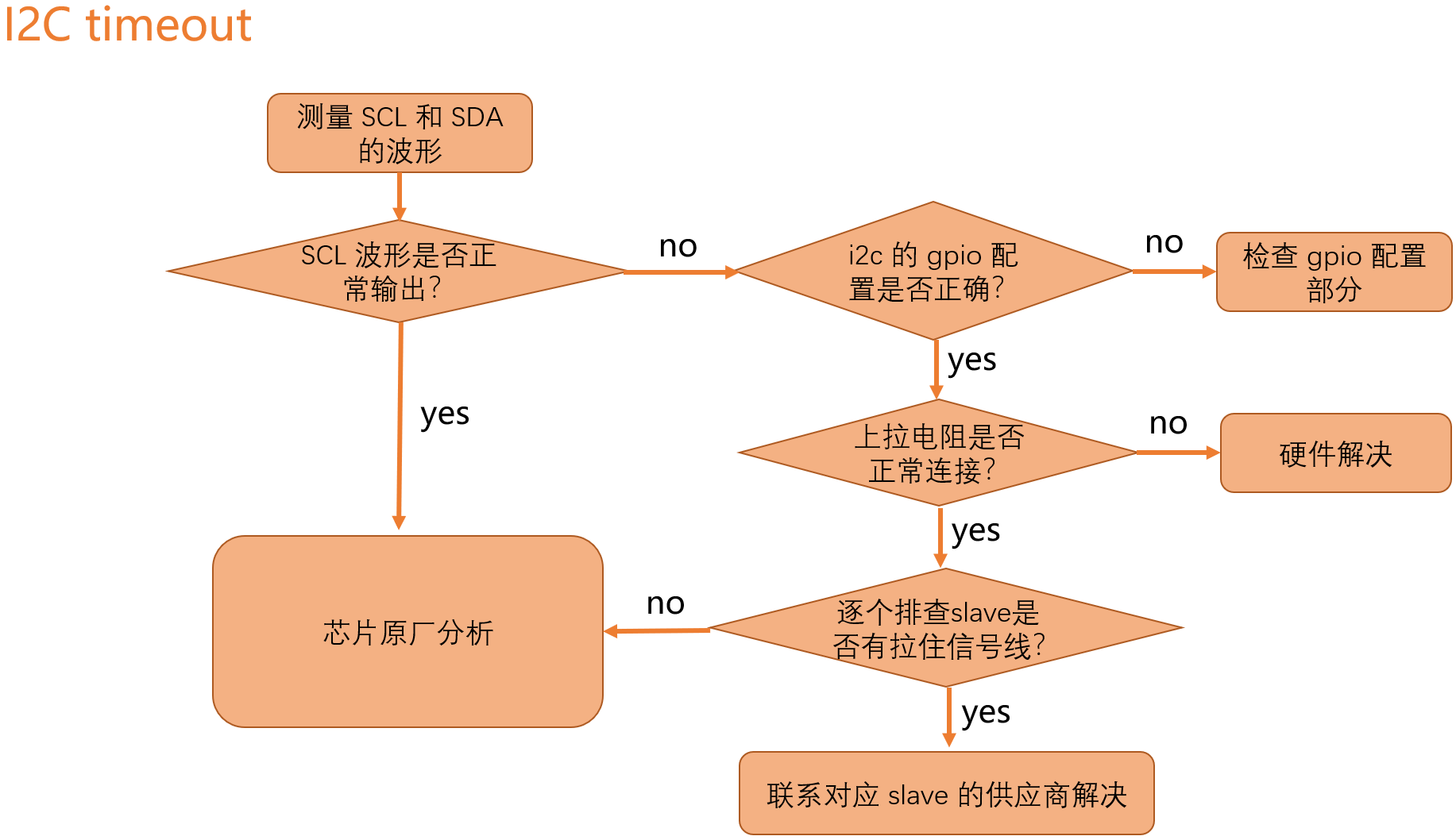
I2C 子系統(四):I2C debug

Three. JS local environment setup
Deep learning: multi-layer perceptron and XOR problem (pytoch Implementation)
![MySQL practice 45 [global lock and table lock]](/img/23/fd58c185ae49ed6c04f1a696f10ff4.png)
MySQL practice 45 [global lock and table lock]
随机推荐
open file in 'w' mode: IOError: [Errno 2] No such file or directory
js根据树结构查找某个节点的下面的所有父节点或者子节点
[leectode 2022.2.15] lucky numbers in the matrix
Réglez la hauteur et lancez le système. Currenttimemillis catton
从输入URL到页面展示这中间发生了什么?
VS 2019 配置tensorRT生成engine
el-tree搜索方法使用
TCP 三次握手和四次挥手机制,TCP为什么要三次握手和四次挥手,TCP 连接建立失败处理机制
idea 加载不了应用市场解决办法(亲测)
别再用 System.currentTimeMillis() 统计耗时了,太 Low,StopWatch 好用到爆!
The XML file generated by labelimg is converted to VOC format
Pat class B "1104 forever" DFS optimization idea
Idea set method call ignore case
TCP handshake three times and wave four times. Why does TCP need handshake three times and wave four times? TCP connection establishes a failure processing mechanism
Use of check boxes: select all, deselect all, and select some
The idea setting code is in UTF-8 idea Properties configuration file Chinese garbled
Pytoch configuration
Use of El tree search method
I2C 子系统(四):I2C debug
[Chongqing Guangdong education] cultural and natural heritage reference materials of China University of Geosciences (Wuhan)